Геометрический смысл частных производных функции двух переменных

Пусть функция z=f(x,y) имеет частные производные 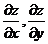в точке M₀(x₀,y₀) и пусть график этой функции представлен некоторой поверхностью (G) (рис. 5.4).

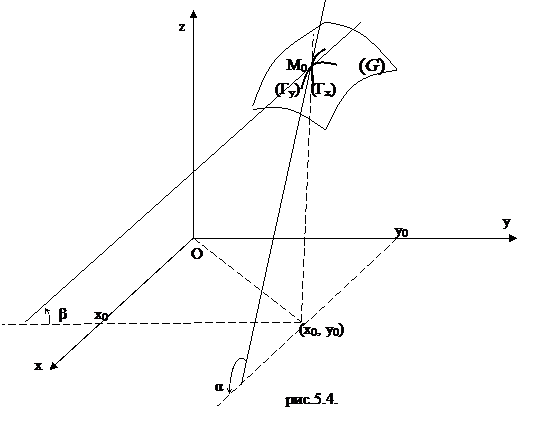
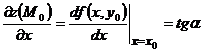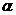Рассечём поверхность (G) плоскостью y=y₀. Графиком функции z=f(x,y₀) является кривая (Г_x) на этой поверхности. Согласно геометрическому смыслу производной функции одной переменной , где -угол наклона касательной к графику (Г_х) функции f(x,y₀) в точке (x_0,y₀,f(x₀,y₀)).

Аналогично 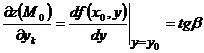, где β- угол наклона касательной к графику (Г_y) функции f(x,y₀) в точке (x_0,y₀,f(x₀,y₀). В этом и состоит геометрический смысл частных производных функции двух переменных.

Дифференциал функции двух переменных

Определение 5.10.

Пусть функция z=f(x,y) задана в некоторой окрестности точки M₀(x₀,y₀).

Полным приращением функции f(x,y) в этой точке называется выражение .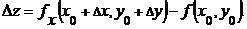

Теорема 5.1.

Если функция f(x,y) имеет непрерывные частные производные в точке М₀(х₀,у₀), то верна следующая формула: 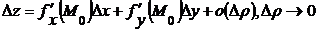где .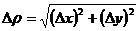

Определение 5.11.

Дифференциалом функции f(x,y) в точке М₀ (х₀,у₀) называется линейная функция 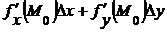относительно двух аргументов .

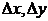Обозначение: 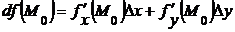. (Другое обозначение: dz).

С учетом введённого понятия дифференциала формула из теоремы 5.1 может быть записана следующим образом: 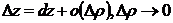или в развёрнутом виде .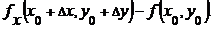

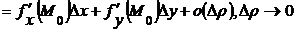Замечание 5.6.

Отбросив в последнем равенстве слагаемое 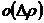, получим приближённое равенство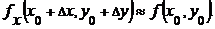 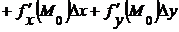. Его можно использовать для вычисления приближенного значения 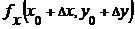при малых 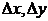, если известны значения , .

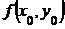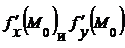Пример 5.4.

Вычислим приближенно .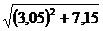

Для этого рассмотрим функцию f(x, y)= 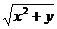. Возьмем число х₀ = 3, близкое к х = 3,05, и число у₀ = 7, близкое к у = 7,15, тогда х = х – х₀ = 0,05, 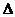у = у – у₀ = 0,15.

Найдем частные производные функции f(x, y):

f'_x = 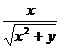, f'_y = 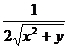, откуда f'_x(3; 7) = 0,75, f'_y(3; 7) = 0,125.

Таким образом,

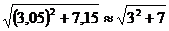+ 0,75·0,05+0,125·0,15 = 4,05625.

Частные производные высших порядков функции двух переменных

Определение 5.12.

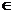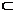Предположим, что функция f(x, y) имеет частную производную f'_x(x, y) по аргументу х в любой точке (х, у) Х /R².

Если функция f'_x(х, у) имеет в точке (х, у) 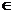Х частную производную по аргументу х, то эта производная называется частной производной второго порядка функции f(x, y) по аргументу х в точке (х, у).

Обозначение: f''_xx = (f'_x)'_x.

(Другие обозначения: z''_xx, ).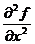

Аналогично определяются другие частные производные второго порядка, которые обозначаются f''_xy, f''_yx, f''_yy.

(Другие обозначения: z''_xy, z''_yx, z''_yy или ).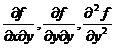

При этом частные производные по одному и тому же аргументу называются чистыми производными, а частные производные по разным аргументам – смешанными производными.

Теорема 5.2 (о равенстве смешанных производных).

Если частные производные второго порядка функции f(x, y) непрерывны в точке (х, у), то в этой точке f''_xy = f''_yx.

Замечание 5.7.

Для функции f(x, y) также могут быть определены частные производные третьего, четвертого, пятого порядка и т.д. Частные производные начиная со второй называются частными производными высших порядков.

Пример 5.5.

Для функции z = x³ – x²y² + 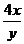найдем частные производные z''_xх, z''_ху, z''_yх, z''_уy, z'''_хyy.

Найдем частные производные первого порядка:

z'_x = 3x² – 2xy² + ,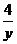

z'_y = -2x²y - 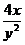, откуда

z''_хх = 6х – 2у²,

z''_ху = -4ху - ,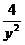

z''_ух = -4ху - ,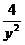

z''_уу = -2х² + ,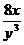

z'''_хуу = (z''_ху)'_у = -4х + .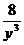

Отметим, что z''_ху = z''_ух, так как для этих смешанных производных выполнены условия теоремы 5.2.

Экстремумы функции

Определение 5.13.

Точка М₀ называется точкой минимума (точкой максимума) функции f(M), если в некоторой окрестности О_δ(М₀) точки М₀ выполняется неравенство f(M) > f(M₀) (f(M) < f(M₀)) при всех М 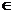О_δ(М₀), М ≠ М₀.

Точки минимума и максимума называются точками экстремума функции f(M), а значения функции в этих точках – экстремумами (минимумами или максимумами).

Теорема 5.3 (необходимые условия экстремума функции).

Если функция f(M) = f(x_1, x₂, …, x_n) имеем в точке М₀ экстремум и существует частная производная 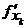(M₀), то эта производная равна нулю.

Точки, в которых все частные производные равны 0, а также те точки, в которых некоторые частные производные не существуют, называются точками, подозрительными на экстремум.

Пример 5.6.

Для функции u = x³ + y² + z² + 12xy + 2z найдем точки, подозрительные на экстремум.

Имеем 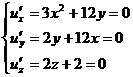, откуда получим , .

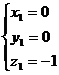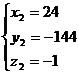Таким образом, данная функция имеет две точки, подозрительные на экстремум: М₁(0; 0; -1), М₂(24; -144; -1).

Достаточные условия экстремума сформулируем для функции двух переменных.

Теорема 5.4 (достаточные условия экстремума функции).

Пусть функция f(x, y) определена в некоторой окрестности, точки (х_0, у₀), причем f'_x(x_0, y₀) = f'_y(x₀, y₀) = 0, а также имеем в этой точке непрерывные частные производные второго порядка.

Обозначим f''_xx(x_0, y₀) = A, f''_xy(x_0, y₀) = f''_yx(x_0, y₀) = B, f''_yy(x_0, y₀) = C, тогда:

1) если АС – В² > 0 и А < 0 (A > 0), то в точке (х_0, у₀) функция f(x, y) имеет максимум (минимум);

2) если АС – В² < 0, то в точке (х₀, у₀) функция f(x, y) экстремума не имеет;

3) если АС – В² = 0, то требуется дополнительное исследование.

Пример 5.7.

Исследуем на экстремум функцию z = x³ + y³ – 3xy.

Найдем точки, подозрительные на экстремум:

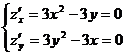, откуда получим М₁(0; 0), М₂(1; 1).

Вычислим частные производные второго порядка: z''_xx = 6x, z''_xy = z''_yx = -3, z''_yy = 6y.

1) В точке М₁(0; 0) имеем А = 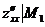= 0, B = -3, C 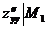= 0.

Поскольку АС – В² = -9 < 0, то в точке М₁(0; 0) экстремума нет.

2) В точке М₂(1; 1) получаем А = 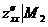= 6, B = -3, C = 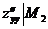= 6.

Следовательно, АС – В² = 27 > 0, причем, A > 0, а это значит, что в точке М₂(1; 1) данная функция имеет минимум z_min = -1.

Глава VI. Неопределенный интеграл