Угол между прямой и плоскостью

!37. Поверхности второго порядка

Поверхностью второго порядка называют поверхность, которая задана алгебраическим уравнением второй степени

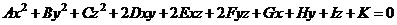, (18.34)

где не все коэффициенты при членах второго порядка одновременно равны нулю.

Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром. Кривая K называется направ-

!44. Функции двух переменных

Рассмотрим функцию 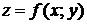, определенную в области 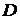на плоскости 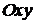, и систему прямоугольных декартовых координат 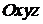. В каждой точке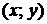

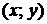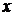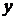Множество пар значений и , при которых определена функция 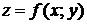, называется областью определения функции, обозначается .

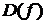В частности, область определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой.

Определение 19.1. Если каждой паре 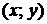из некоторой области их изменения 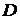, поставлено в соответствие определенное значение величины 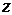, то говорят, что 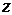есть функция двух независимых переменных 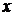и 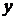. Записывается

.

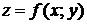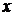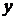При этом и называются независимыми переменными (аргументами), а 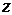- зависимой переменной (функцией).

!45. Предел и непрерывность функции двух переменных

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывность, аналогично случаю функции одной переменной.

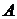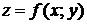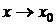Определение 19.3. Число называется пределом функции при и 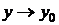(или, что то же самое, при 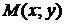® 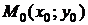), если для любого 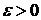существует 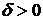такое, что для всех 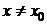и 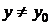и удовлетворяющих неравенству 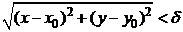выполняется неравенство 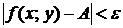. Записывают:

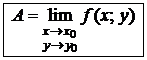
или

.

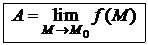Определение 19.4. Функция 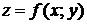(или 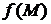) называется непрерывной в точке 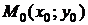, если она:

1) определена в этой точке и некоторой ее окрестности;

2) имеет предел ;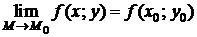

3) этот предел равен значению функции 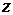в точке 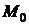, т.е.

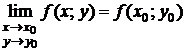или .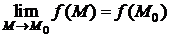

!46. Частные производные ФНП

Рассмотрим линию 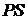пересечения поверхности 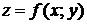с плоскостью 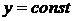, параллельной плоскости 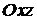. Так как в этой плоскости 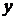сохраняет постоянное значение, то 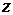вдоль кривой 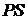будет меняться только в зависимости от изменения 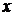. Дадим независимой переменной 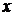приращение 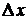, тогда 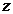получит приращение, которое называется частным приращением 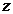по 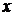и обозначают через 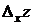(на рисунке отрезок 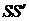), так что

.

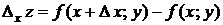Аналогично, если 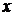сохраняет постоянное значение, а 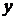получает приращение

параллельной плоскости .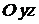

.

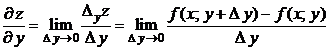Определение 19.6. Частной производной по 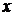от функции 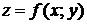называется предел отношения частного приращения 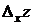по 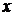к приращению 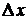при стремлении 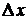к нулю. Обозначается: 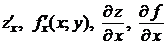. Тогда

.

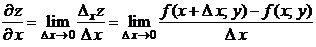Определение 19.7. Частной производной по 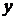от функции 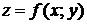называется предел отношения частного приращения 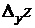по 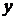к приращению 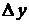при стремлении 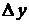к нулю. Обозначается: .

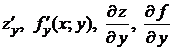!47. Частные производные высших порядков

Пусть имеем функцию двух переменных 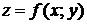. Частные производные 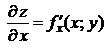и 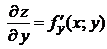, вообще говоря, являются функциями переменных 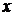и 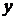. Поэтому от них можно снова находить частные производные. Следовательно, частных производных второго порядка от функции двух переменных четыре, так как каждую из функци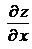й и 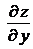можно дифференцировать как по 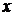, так и по 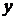. Вторые частные производные обозначают так:

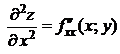: здесь 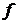дифференцируется последовательно два раза по ;

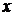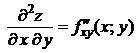: здесь 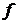дифференцируется последовательно по 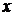, а потом

результат дифференцируется по ;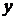

: здесь 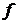дифференцируется последовательно по 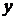, а потом

результат дифференцируется по ;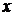

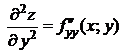: здесь 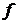дифференцируется последовательно два раза по ;

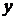Производные второго порядка можно снова дифференцировать как по 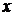, так и по

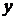. Получим частные производные третьего порядка.

Теорема 19.1 (теорема Шварца). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.

В частности, для 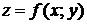имеем .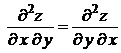

!48. Дифференцируемость и полный дифференциал функции

Пусть функция 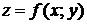определена в некоторой окрестности точки 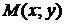. Составим полное приращение функции в точке :

.

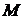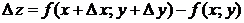Определение 19.8. Функция 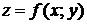называется дифференцируемой в точке 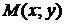, если ее полное приращение в этой точке можно представить в виде

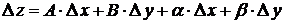, (19.1)

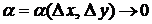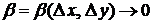где и при 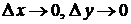. Сумма первых двух слагаемых в равенстве (19.1) представляет собой главную часть приращения функции.

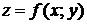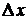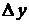Определение 19.9. Главная часть приращения функции , линейная относительно и , называется полным дифференциалом этой функции и обозначается символом :

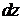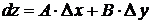. (19.2)

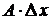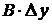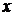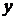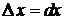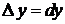Выражения и называются частными дифференциалами. Для независимых переменных и полагают и . Поэтому равенство (19.2) можно представить в виде

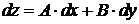. (19.3)

Для функции 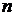переменных 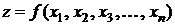полный дифференциал определяется выражением

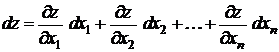. (19.5)

Надо отметить, если функция 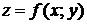дифференцируема в точке 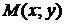, то она непрерывна в этой точке, имеет в ней частные производные 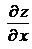и 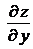, причем 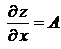, 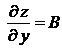. Тогда формула для вычисления полного дифференциала примет вид:

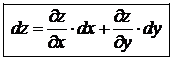. (19.4)

!49. Производная сложной функции. Полная производна

Пусть 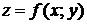- функция двух переменных 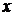и 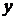, каждая из которых является функцией независимой переменной 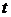, т.е. 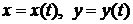. В этом случае функция 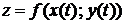является сложной функцией одной независимой переменной 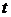, а переменные 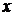и 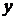будут промежуточными переменными.

Теорема 19.2. Если 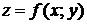- функция, дифференцируемая в точке 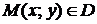, и 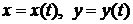- дифференцируемые функции независимой переменной 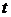, то производная сложной функции 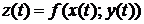вычисляется по формуле:

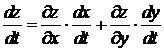. (19.7)

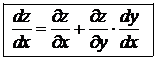. (19.8)

Формула (19.8) называется формулой полной производной.

.
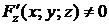