Формулу интегрирования подстановкой
Формулу интегрирования подстановкой

Докажем следующую теорему.
Теорема 16.2. Если 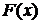 - первообразная функции
- первообразная функции 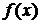 , а
, а  - дифференцируемая функция, то функция
- дифференцируемая функция, то функция  также имеет первообразную, причем
также имеет первообразную, причем
 .
.
Доказательство. По правилу дифференцирования сложной функции
 ,
,
т.е. функция  имеет в качестве одной из своих производных первообразную функцию
имеет в качестве одной из своих производных первообразную функцию  .
.
Следовательно,  .
.
Поскольку  , то
, то
 .
.
Иногда целесообразно подбирать подстановку в виде  , тогда
, тогда
 , где
, где  .
.
Другими словами, формулу (16.2) можно применять справа налево.
!6. Пусть  и
и  - функции, имеющие непрерывные производные. Тогда
- функции, имеющие непрерывные производные. Тогда  . Интегрируя это равенство, получаем
. Интегрируя это равенство, получаем

или
 (16.3)
(16.3)
Формула (16.3) называется формулой интегрирования по частям.
1 группа. Интегралы вида  ,
,  ,
,  , где
, где  - многочлен,
- многочлен,  - число. Удобно положить
- число. Удобно положить  , а за
, а за  обозначить все остальные сомножители.
обозначить все остальные сомножители.
2 группа. Интегралы вида  ,
,  ,
,  ,
,  ,
,  . Удобно положить
. Удобно положить  , а за
, а за  обозначить остальные сомножители.
обозначить остальные сомножители.
3 группа. Интегралы вида  ,
,  , где
, где  и
и  - числа,
- числа,  ,
,  . Применяя формулу (16.3) к любому из указанных интегралов дважды, мы получим для нахождения интеграла уравнение первого порядка, причем за
. Применяя формулу (16.3) к любому из указанных интегралов дважды, мы получим для нахождения интеграла уравнение первого порядка, причем за  можно принимать любой из сомножителей.
можно принимать любой из сомножителей.
!7. Для интегрирования рациональных дробей сформулируем общее правило.
1.Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби.
2.Разложив знаменатель правильной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
3.Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример 16.9. Найти интеграл  .
.
Решение.
 .
.
Методом неопределенных коэффициентов найдем  .
.
 ;
;
 ;
;
 .
.
Составляем и решаем систему линейных уравнений:
 Þ
Þ  Þ
Þ  Þ
Þ  .
.
Далее находим интеграл:

 .
.
!12.  , (17.1)
, (17.1)
где  - длина соответствующего частичного отрезка.
- длина соответствующего частичного отрезка.
Сумма вида (17.1) называется интегральной суммой функции  на отрезке
на отрезке  . Обозначим через l длину наибольшего из частичных отрезков, т.е.
. Обозначим через l длину наибольшего из частичных отрезков, т.е.  ,
,  . Найдем предел интегральной суммы (17.1), когда
. Найдем предел интегральной суммы (17.1), когда  так, что
так, что  .
.
Определенным интегралом от функции  на отрезке
на отрезке  называется конечный предел ее интегральной суммы, когда число частичных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Определенный интеграл обозначается символом
называется конечный предел ее интегральной суммы, когда число частичных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Определенный интеграл обозначается символом  . Таким образом,
. Таким образом,
 . (17.2)
. (17.2)
Числа  и
и  называются соответственно нижним и верхним пределами интегрирования,
называются соответственно нижним и верхним пределами интегрирования, 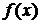 - подынтегральной функцией,
- подынтегральной функцией,  - подынтегральное выражение,
- подынтегральное выражение, 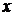 - переменной интегрирования, отрезок
- переменной интегрирования, отрезок  - областью (отрезком) интегрирования.
- областью (отрезком) интегрирования.
Функция  , для которой на отрезке
, для которой на отрезке  существует определенный интеграл
существует определенный интеграл  , называется интегрируемой на этом отрезке.
, называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла (без доказательства).
Теорема 17.1 (Коши). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то определенный интеграл
, то определенный интеграл  существует.
существует.
Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции 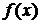 на отрезке
на отрезке  численно равен площади криволинейной трапеции.
численно равен площади криволинейной трапеции.
Физический смысл определенного интеграла: работа переменной силы  , которая есть непрерывная функция, действующая не отрезке
, которая есть непрерывная функция, действующая не отрезке  , равна определенному интегралу от величины силы
, равна определенному интегралу от величины силы 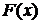 , взятому на отрезке
, взятому на отрезке  .
.
!13. Свойство 1.Если  и функция
и функция 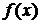 интегрируема на отрезке
интегрируема на отрезке  , то
, то
 .
.
Свойство 2.Если функции  и
и  интегрируемы на оaтрезке
интегрируемы на оaтрезке  , тогда интегрируема на
, тогда интегрируема на  их сумма и
их сумма и
 .
.
т.е. интеграл суммы равен сумме интегралов.
Доказательство.

 . ,
. ,
Свойство 3.
 .
.
Свойство 4 (аддитивности).Если функция 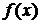 интегрируема на отрезке
интегрируема на отрезке  и
и  , то
, то
 ,
,
т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка.
Свойство 5 (теорема о среднем).Если функция 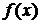 непрерывна на отрезке
непрерывна на отрезке  , то существует точка
, то существует точка  , такая, что справедливо равенство
, такая, что справедливо равенство
 . (17.3)
. (17.3)
!14. Формула Ньютона-Лейбница
Пусть функция 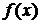 непрерывна на отрезке
непрерывна на отрезке  . Тогда она интегрируема и на любом отрезке
. Тогда она интегрируема и на любом отрезке  , где
, где  , т.е. для любого
, т.е. для любого  имеет смысл интеграл
имеет смысл интеграл  . Рассмотрим функцию
. Рассмотрим функцию
 , (17.4)
, (17.4)
которая определена на отрезке  и называется интегралом с переменным верхним пределом.
и называется интегралом с переменным верхним пределом.
!15. Интеграл с бесконечным промежутком интегрирования
Определение 17.1. Пусть функция 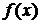 непрерывна на промежутке
непрерывна на промежутке  . Если существует конечный предел
. Если существует конечный предел  , то его называют сходящимся несобственным интегралом первого рода и обозначают
, то его называют сходящимся несобственным интегралом первого рода и обозначают  , т.е.
, т.е.
 . (17.6)
. (17.6)
Если же указанный предел не существует или он бесконечен, то говорят, что интеграл  расходится.
расходится.
Определение 17.2. Пусть функция 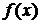 непрерывна на промежутке
непрерывна на промежутке  и имеет бесконечный разрыв при
и имеет бесконечный разрыв при  . Если существует конечный предел
. Если существует конечный предел  , где
, где 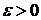 , то его называют сходящимся несобственным интегралом второго рода и обозначают
, то его называют сходящимся несобственным интегралом второго рода и обозначают  , т.е.
, т.е.
 . (17.7)
. (17.7)
!16. Декартова система координат
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей.

Система координат обозначается  , а плоскость, в которой расположена система координат, называют координатной плоскостью.
, а плоскость, в которой расположена система координат, называют координатной плоскостью.
Преобразование системы координат
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.
1. Параллельный перенос осей координат
2. Поворот осей координат
Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остается неизменным
17. Полярная система координат
Декартовая система координат дает удобный, но не единственный способ определения положения точек плоскости при помощи чисел.
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой  , которая называется полюсом, лучом
, которая называется полюсом, лучом  , называемым полярной осью, и единичным вектором
, называемым полярной осью, и единичным вектором  того же направления, что и луч
того же направления, что и луч  .
.

Числа r и j называются полярными координатами точки  , пишут
, пишут  , при этом r называют полярным радиусом, j - полярным углом.
, при этом r называют полярным радиусом, j - полярным углом.
Для получения всех точек плоскости достаточно полярный угол j ограничить промежутком  (или
(или  ), а полярный радиус -
), а полярный радиус -  . В этом случае каждой точке плоскости (кроме
. В этом случае каждой точке плоскости (кроме  ) соответствует единственная пара чисел r и j, и обратно.
) соответствует единственная пара чисел r и j, и обратно.
Установим связь между прямоугольными и полярными координатами.

 , где
, где  .
.
Если эти формулы разрешить относительно r и j, то получим следующие формулы:
 .
.
Чтобы определить величину угла j, лучше использовать формулу  , при этом устанавливается (по знакам
, при этом устанавливается (по знакам 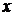 и
и 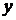 ) четверть, в которой лежит искомый угол, и учитывается, что
) четверть, в которой лежит искомый угол, и учитывается, что  (или
(или  ).
).
!18. Линии на плоскости
Метод координат на плоскости используется в геометрии для изучения линий. Линия (или кривая) плоскости задается как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, прямая, окружность, парабола, синусоида и т.д.
Линию (кривую) на плоскости можно задать:
1) уравнением в декартовой системе  ;
;
2) уравнением в полярной системе координат;
3) параметрически;
4) векторным уравнением.
 Уравнением линии (или кривой) на плоскости
Уравнением линии (или кривой) на плоскости  называется такое уравнение
называется такое уравнение  с двумя переменными, которому удовлетворяют координаты
с двумя переменными, которому удовлетворяют координаты 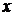 и
и 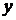 каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
 Уравнение
Уравнение  называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
 Линию на плоскости можно задать параметрически при помощи двух уравнений:
Линию на плоскости можно задать параметрически при помощи двух уравнений:
 ,
,
где 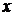 и
и 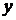 - координаты произвольной точки
- координаты произвольной точки 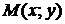 , лежащей на данной линии, а
, лежащей на данной линии, а 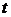 - переменная, называемая параметром; параметр
- переменная, называемая параметром; параметр 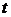 определяет положение точки
определяет положение точки 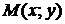 на плоскости.
на плоскости.
Если параметр 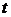 изменяется, то точка на плоскости перемещается, описывая данную линию. Система из двух уравнений
изменяется, то точка на плоскости перемещается, описывая данную линию. Система из двух уравнений  называется параметрическими уравнениями линии.
называется параметрическими уравнениями линии.
 Линию на плоскости можно задать векторным уравнением
Линию на плоскости можно задать векторным уравнением  , где
, где 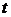 - скалярный переменный параметр. Каждому значению
- скалярный переменный параметр. Каждому значению  соответствует определенный вектор
соответствует определенный вектор  плоскости. При изменении параметра
плоскости. При изменении параметра 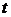 конец вектора
конец вектора  описывает
описывает

Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линии – траекторией точки, параметр 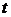 при этом есть время.
при этом есть время.
В аналитической геометрии на плоскости возникают две основные задачи:
1) зная геометрические свойства кривой, найти ее уравнение;
2) зная уравнение кривой, изучить ее форму и свойства.
!19. Общее уравнение прямой
Положение прямой  на плоскости вполне определено, если известны точка
на плоскости вполне определено, если известны точка  , через которую она проходит, и ненулевой вектор
, через которую она проходит, и ненулевой вектор  , перпендикулярный к этой прямой.
, перпендикулярный к этой прямой.
Постановка задачи: Составить уравнение прямой, проходящей через точку  , и перпендикулярную вектору
, и перпендикулярную вектору  . Вектор
. Вектор  называется нормальным вектором прямой.
называется нормальным вектором прямой.

 . (18.1)
. (18.1)
Соотношение (18.1) удовлетворяет координатам тех и только тех точек плоскости  , которые принадлежат прямой
, которые принадлежат прямой  . Формула (18.1) называется уравнением прямой с нормальным вектором
. Формула (18.1) называется уравнением прямой с нормальным вектором  и проходящей через точку
и проходящей через точку  .
.
Раскрыв скобки в уравнении (18.1), получим
 , (18.2)
, (18.2)
где  . Уравнение (18.2) называется общим уравнением прямой с нормальным вектором
. Уравнение (18.2) называется общим уравнением прямой с нормальным вектором  .
.
1) при  уравнение
уравнение  определяет прямую, проходящую через начала координат;
определяет прямую, проходящую через начала координат;
2) при  уравнение
уравнение  Û
Û  определяет прямую, перпендикулярную к вектору
определяет прямую, перпендикулярную к вектору  и параллельную оси
и параллельную оси  . Если
. Если  , то уравнение
, то уравнение  определяет ось
определяет ось  ;
;
3) при  уравнение
уравнение  Û
Û  определяет прямую, перпендикулярную к вектору
определяет прямую, перпендикулярную к вектору  и параллельную оси
и параллельную оси  . Если
. Если  , то уравнение
, то уравнение  определяет ось
определяет ось  .
.
!20. Уравнение прямой с угловым коэффициентом
 (18.3)
(18.3)
называется уравнением прямой с угловым коэффициентом k.
Уравнение (18.3) можно получить из общего уравнения (18.2) при  . Действительно, из (18.2) имеем
. Действительно, из (18.2) имеем  . Обозначив
. Обозначив  , придем к уравнению (18.3).
, придем к уравнению (18.3).
Выясним геометрический смысл углового коэффициента  прямой
прямой  .
.

или
 .
.
Итак,  и
и  . Сравнивая два уравнения, получаем
. Сравнивая два уравнения, получаем  .
.
Угловой коэффициент k прямой  численно равен тангенсу угла наклона этой прямой к оси
численно равен тангенсу угла наклона этой прямой к оси  , т.е.
, т.е.  .
.
 . (18.4)
. (18.4)
Равенство (18.4) называется уравнением прямой с угловым коэффициентом, проходящей через заданную точку  .
.
21. Каноническое уравнение прямой
Постановка задачи: Составить уравнение прямой, проходящей через точку  , и параллельной вектору
, и параллельной вектору  . Вектор
. Вектор  называется направляющим вектором прямой.
называется направляющим вектором прямой.
|

Равенство (18.5) называется каноническим уравнением прямой на плоскости.
Двух плоскостей
Пусть две плоскости P1 и P2 заданы своими общими уравнениями:
 ;
;
 .
.
Если плоскости P1 и P2 параллельны, то параллельны и их нормальные векторы  и
и  . Отсюда, учитывая условие параллельности векторов, получаем условие параллельности двух плоскостей:
. Отсюда, учитывая условие параллельности векторов, получаем условие параллельности двух плоскостей:
 Þ
Þ  Û
Û  .
.
Если  , то
, то  и, значит, условие перпендикулярности двух плоскостей имеет вид:
и, значит, условие перпендикулярности двух плоскостей имеет вид:
 Þ
Þ  Û
Û  Û
Û  .
.
Метод И.Бернулли
Решение уравнения (20.5) находится в виде произведения двух других функций, т.е. с помощью подстановки  , где
, где  и
и  - неизвестные функции от
- неизвестные функции от 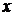 . Тогда
. Тогда  . Подставляя выражения
. Подставляя выражения 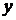 и
и  в уравнение (20.5), получаем
в уравнение (20.5), получаем

или
 . (*)
. (*)
58.
формулу интегрирования подстановкой

Докажем следующую теорему.
Теорема 16.2. Если 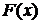 - первообразная функции
- первообразная функции 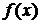 , а
, а  - дифференцируемая функция, то функция
- дифференцируемая функция, то функция  также имеет первообразную, причем
также имеет первообразную, причем
 .
.
Доказательство. По правилу дифференцирования сложной функции
 ,
,
т.е. функция  имеет в качестве одной из своих производных первообразную функцию
имеет в качестве одной из своих производных первообразную функцию  .
.
Следовательно,  .
.
Поскольку  , то
, то
 .
.
Иногда целесообразно подбирать подстановку в виде  , тогда
, тогда
 , где
, где  .
.
Другими словами, формулу (16.2) можно применять справа налево.
!6. Пусть  и
и  - функции, имеющие непрерывные производные. Тогда
- функции, имеющие непрерывные производные. Тогда  . Интегрируя это равенство, получаем
. Интегрируя это равенство, получаем

или
 (16.3)
(16.3)
Формула (16.3) называется формулой интегрирования по частям.
1 группа. Интегралы вида  ,
,  ,
,  , где
, где  - многочлен,
- многочлен,  - число. Удобно положить
- число. Удобно положить  , а за
, а за  обозначить все остальные сомножители.
обозначить все остальные сомножители.
2 группа. Интегралы вида  ,
,  ,
,  ,
,  ,
,  . Удобно положить
. Удобно положить  , а за
, а за  обозначить остальные сомножители.
обозначить остальные сомножители.
3 группа. Интегралы вида  ,
,  , где
, где  и
и  - числа,
- числа,  ,
,  . Применяя формулу (16.3) к любому из указанных интегралов дважды, мы получим для нахождения интеграла уравнение первого порядка, причем за
. Применяя формулу (16.3) к любому из указанных интегралов дважды, мы получим для нахождения интеграла уравнение первого порядка, причем за  можно принимать любой из сомножителей.
можно принимать любой из сомножителей.
!7. Для интегрирования рациональных дробей сформулируем общее правило.
1.Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби.
2.Разложив знаменатель правильной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
3.Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример 16.9. Найти интеграл  .
.
Решение.
 .
.
Методом неопределенных коэффициентов найдем  .
.
 ;
;
 ;
;
 .
.
Составляем и решаем систему линейных уравнений:
 Þ
Þ  Þ
Þ  Þ
Þ  .
.
Далее находим интеграл:

 .
.
!12.  , (17.1)
, (17.1)
где  - длина соответствующего частичного отрезка.
- длина соответствующего частичного отрезка.
Сумма вида (17.1) называется интегральной суммой функции  на отрезке
на отрезке  . Обозначим через l длину наибольшего из частичных отрезков, т.е.
. Обозначим через l длину наибольшего из частичных отрезков, т.е.  ,
,  . Найдем предел интегральной суммы (17.1), когда
. Найдем предел интегральной суммы (17.1), когда  так, что
так, что  .
.
Определенным интегралом от функции  на отрезке
на отрезке  называется конечный предел ее интегральной суммы, когда число частичных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Определенный интеграл обозначается символом
называется конечный предел ее интегральной суммы, когда число частичных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Определенный интеграл обозначается символом  . Таким образом,
. Таким образом,
 . (17.2)
. (17.2)
Числа  и
и  называются соответственно нижним и верхним пределами интегрирования,
называются соответственно нижним и верхним пределами интегрирования, 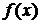 - подынтегральной функцией,
- подынтегральной функцией,  - подынтегральное выражение,
- подынтегральное выражение, 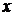 - переменной интегрирования, отрезок
- переменной интегрирования, отрезок  - областью (отрезком) интегрирования.
- областью (отрезком) интегрирования.
Функция  , для которой на отрезке
, для которой на отрезке  существует определенный интеграл
существует определенный интеграл  , называется интегрируемой на этом отрезке.
, называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла (без доказательства).
Теорема 17.1 (Коши). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то определенный интеграл
, то определенный интеграл  существует.
существует.
Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции 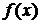 на отрезке
на отрезке  численно равен площади криволинейной трапеции.
численно равен площади криволинейной трапеции.
Физический смысл определенного интеграла: работа переменной силы  , которая есть непрерывная функция, действующая не отрезке
, которая есть непрерывная функция, действующая не отрезке  , равна определенному интегралу от величины силы
, равна определенному интегралу от величины силы 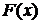 , взятому на отрезке
, взятому на отрезке  .
.
!13. Свойство 1.Если  и функция
и функция 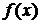 интегрируема на отрезке
интегрируема на отрезке  , то
, то
 .
.
Свойство 2.Если функции  и
и  интегрируемы на оaтрезке
интегрируемы на оaтрезке  , тогда интегрируема на
, тогда интегрируема на  их сумма и
их сумма и
 .
.
т.е. интеграл суммы равен сумме интегралов.
Доказательство.

 . ,
. ,
Свойство 3.
 .
.
Свойство 4 (аддитивности).Если функция 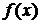 интегрируема на отрезке
интегрируема на отрезке  и
и  , то
, то
 ,
,
т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка.
Свойство 5 (теорема о среднем).Если функция 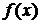 непрерывна на отрезке
непрерывна на отрезке  , то существует точка
, то существует точка  , такая, что справедливо равенство
, такая, что справедливо равенство
 . (17.3)
. (17.3)
!14. Формула Ньютона-Лейбница
Пусть функция 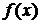 непрерывна на отрезке
непрерывна на отрезке  . Тогда она интегрируема и на любом отрезке
. Тогда она интегрируема и на любом отрезке  , где
, где  , т.е. для любого
, т.е. для любого  имеет смысл интеграл
имеет смысл интеграл  . Рассмотрим функцию
. Рассмотрим функцию
 , (17.4)
, (17.4)
которая определена на отрезке  и называется интегралом с переменным верхним пределом.
и называется интегралом с переменным верхним пределом.
!15. Интеграл с бесконечным промежутком интегрирования
Определение 17.1. Пусть функция 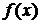 непрерывна на промежутке
непрерывна на промежутке  . Если существует конечный предел
. Если существует конечный предел  , то его называют сходящимся несобственным интегралом первого рода и обозначают
, то его называют сходящимся несобственным интегралом первого рода и обозначают  , т.е.
, т.е.
 . (17.6)
. (17.6)
Если же указанный предел не существует или он бесконечен, то говорят, что интеграл  расходится.
расходится.
Определение 17.2. Пусть функция 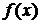 непрерывна на промежутке
непрерывна на промежутке  и имеет бесконечный разрыв при
и имеет бесконечный разрыв при  . Если существует конечный предел
. Если существует конечный предел  , где
, где 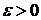 , то его называют сходящимся несобственным интегралом второго рода и обозначают
, то его называют сходящимся несобственным интегралом второго рода и обозначают  , т.е.
, т.е.
 . (17.7)
. (17.7)
!16. Декартова система координат
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей.

Система координат обозначается  , а плоскость, в которой расположена система координат, называют координатной плоскостью.
, а плоскость, в которой расположена система координат, называют координатной плоскостью.
Преобразование системы координат
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.
1. Параллельный перенос осей координат
2. Поворот осей координат
Под поворотом осей координат понимают та

 . Найдем координаты вектора
. Найдем координаты вектора  :
:  .
.  . Тогда
. Тогда  . (18.5)
. (18.5)