Формула остроградского-грина.
Связь между дв. Инт. По области Д и криволин. Инт. По области L устанавливают формулу Остроградского-Грина.
Пусть на плоскости OXY задана область Д огр. Кривой пересекающееся с прямыми параллельными корд. Осям не более чем в 2 точках, т. е. область Д правильная.
Т1.Если ф. P(x,y), Q(x,y) непрерывно вместе со своими чанными производными 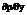 ,
,
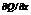 области Д то справедлива форм.
области Д то справедлива форм. 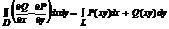 (ф.Остр.-Гр.)
(ф.Остр.-Гр.)
, L граница области Д и интегрирование вдоль кривой L производится в положительном направлении.До- во.
Т2.Если 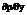 =
= 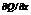 (2), то подинтегр. Выражение P*dx+Q*dy явл. Полным диф. Функции U=U(x,y).
(2), то подинтегр. Выражение P*dx+Q*dy явл. Полным диф. Функции U=U(x,y).
P*dx+Q*dy =U(x.y)
Удовлетворяет условию (2) можно найти используя ф. 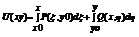
Зам.1 Чтобы не спутать переменную интегр. X с верхним преднлом ее обозн. Другой буквой.
Зам. 2 в качестве нач точки(x0,Y0) обычно берут точку (0.0)
Условие независимости криволинейного инт. 2-го рода от пути интегр.
Пусть т. А (X1, Y1), В(X2, Y2),. Пусть произв. точки области Д. Точки А и B можно соеденить различными линиями. По каждой из них кр. Инт. 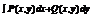 будет иметь свое значение если же значение по всем кривым одинаково, то интеграл не зависит, от вида пути инт., в этам сл достаточно отметить первонач. Точку А (X1, Y1) и конечную В(X2, Y2).
будет иметь свое значение если же значение по всем кривым одинаково, то интеграл не зависит, от вида пути инт., в этам сл достаточно отметить первонач. Точку А (X1, Y1) и конечную В(X2, Y2).
Т. Для того, чтобы кр. Инт. 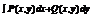
Не зависит от пути инт. Области Д в кот. Ф. P(X,Y), Q(X,Y) непрерывны вместе со своими производными и необходимо, чтобы в каждой точке области 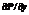 =
= 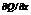 Док-во
Док-во
Кр. Инт. 2-го рода не зависит отпути интегрирования
Зам. 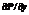 =
= 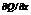 отсюда получаем, что
отсюда получаем, что 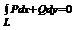
Пов. Инт. 1-го рода.Его св. и выч.
Пусть в точках пов. S С ПЛ. S пространства oxyz опред. Непрерывная ф. f(x,y.z) .
Разобьем пов. S на n частей Si, ПЛ. КАЖДОЙ ЧАСТИ дельта Si, а диаметр Di i=1..m в каждой части Si выберем произвольную точку Mi от (xi, yi, zi) и cоставим сумму 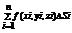 . Сумма называется интегральной для ф. f(x,y.z) по поверхности S если при
. Сумма называется интегральной для ф. f(x,y.z) по поверхности S если при 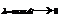 интегр. Сумма имеет предел, то он наз. Пов интегралом 1-го родаот ф. f(x,y.z) по поверхности S и обозначается
интегр. Сумма имеет предел, то он наз. Пов интегралом 1-го родаот ф. f(x,y.z) по поверхности S и обозначается 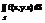 =
= 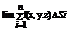
Свойства пов. Инт.
1) 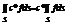 , с=const
, с=const
2) 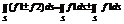 3) S=s1+s2, Тогда
3) S=s1+s2, Тогда 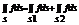
 4) f1<=f2 , т о
4) f1<=f2 , т о 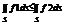 5)
5) 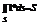 6)
6) 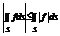 7) Ф. f непрерывна на поверхности S , то на этой поверхности сущ. Точка M(x0,y0,z0)
7) Ф. f непрерывна на поверхности S , то на этой поверхности сущ. Точка M(x0,y0,z0) 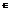 S, такая , что
S, такая , что 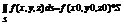 .
.
Выч пов инт 1-го родасводиться к вычисленею2-го инт по обл Д, кот явл проекцией пов S на плоскость oxy, если пов s задана Ур z=z(x,y) то по винт равен 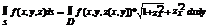 .
.
Если S задано в виде y=y(x, z), то …
Пов инт 2-го рода
Пусть задана двусторонняя пов, после обхода такой пов не пересекая ее границы направление нормали к ней не меняется. Односторонныя пов: является Лист Мебиуса. Пусть в точке рассматриваемой двусторонней поверхности S в прстранстве oxyz определена ф. F(x,y,z). Выбронную сторону поверхности разбиваем на части Si i=1..m и проектируем их на корд плоскости. При этом пл пов 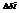 ,берем со знаком «+», если выбрана верхняя сторона пов ( если нормаль
,берем со знаком «+», если выбрана верхняя сторона пов ( если нормаль  образует острый угол с oz, выб со зн «–» если выбрана нижняя сторона пов( ТУПОЙ УГОЛ)). Составим инт сумму
образует острый угол с oz, выб со зн «–» если выбрана нижняя сторона пов( ТУПОЙ УГОЛ)). Составим инт сумму 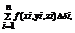 Где
Где 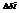 – пл пов Si –части при
– пл пов Si –части при 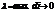 если он сущ и не зависит от способа разбиения поверхности на части и от выбора точек в них, наз по инт 2-ого рода от ф. f(x,y,z) по пов s и обозначается:
если он сущ и не зависит от способа разбиения поверхности на части и от выбора точек в них, наз по инт 2-ого рода от ф. f(x,y,z) по пов s и обозначается: 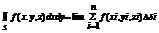 по опред пов интеграл будет = пределу интегр суммы. Аналогично опред инт по пов s
по опред пов интеграл будет = пределу интегр суммы. Аналогично опред инт по пов s
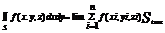
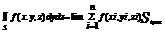 , тогда общим видоим пов инт 2-го рода служит инт
, тогда общим видоим пов инт 2-го рода служит инт 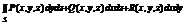 где P, Q, R непрерывные функции опред в точках двусторонней пов s. Если S замкнутая пов, то по инт по внешней стороне обозначается
где P, Q, R непрерывные функции опред в точках двусторонней пов s. Если S замкнутая пов, то по инт по внешней стороне обозначается 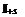 и по внутренней стороне
и по внутренней стороне 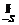 .
.
Свойства по винт 2-го рода
1) Пов инт 2-го рода изм знак при перемене стороны пов 2) пост множетель можно выносить за знак инт 3) пов инт от суммы ф.равен суммен пов инт от слагаемых 4) по винт от всей пов S =S1+S2 равен сумме инт по ее частям S1и S2, если S1 иS2 пересек лишь по границе их разеляющей 5) если S1, S2 ,S3 цилиндрические поверхности с обр параллельными oz, ox, oy соотв, то пов инт: 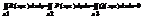
Выч по винт 2-го рода
Пусть R(xyz) непрерывна во всех точках пов s задано Ур z=z(xy), где Z(xy) непрерывна в замкнутой области Дxy 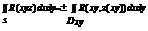 Знак «+» если брать верхнюю сторону поверхности S, «–» если нижнюю.
Знак «+» если брать верхнюю сторону поверхности S, «–» если нижнюю.
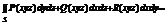
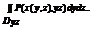 Замеч Можно показать справедливость равенств dxdy=cos
Замеч Можно показать справедливость равенств dxdy=cos 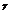 ds, dydz=cos
ds, dydz=cos 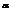 ds, dxdz=cos
ds, dxdz=cos 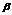 ds. Где ds элемент площади пов S , а cos
ds. Где ds элемент площади пов S , а cos 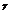 , cos
, cos 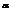 cos
cos 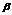 напр cos нармали n. Выбранной стороны пов.
напр cos нармали n. Выбранной стороны пов.
