Тема 6 Повторные независимые испытания

Задача 1. Вероятность всхожести семян пшеницы равна 0,9. Какова вероятность того, что из четырех посеянных семян взойдут не менее трех?

Пусть событие А — из 4 семян взойдут не менее 3 семян; событие В — из 4 семян взойдут 3 семени; событие С — из 4 семян взойдут 4 семени. По теореме сложения вероятностей несовместных событий Р(А)=Р(В)+Р(С).

Вероятности P(B) и Р(С) определим по формуле Бернулли, применяемой в следующем случае. Пусть проводится серия n независимых испытаний при каждом из которых вероятность наступления события постоянна и равна р, а вероятность наступления этого события равна q=1 — р. Тогда вероятность того, что событие А в n испытаниях появится ровно k раз, вычисляется по формуле Бернулли: Pn(k)=Ckn pkqn-k,где 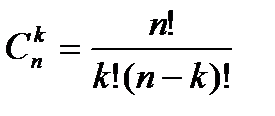- число сочетаний из n элементов по k.

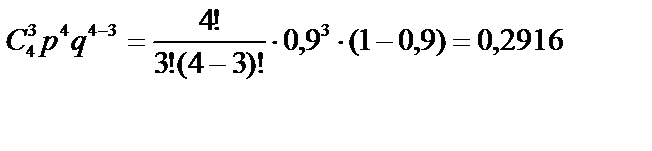Тогда

Р(В) =Р₄(3) =

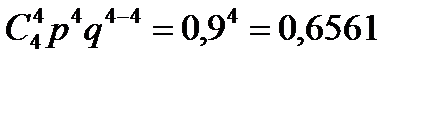Р(С) =Р₄(4) =

Искомая вероятность Р (А)=О,2916+0,6561 = 0,9477.

Задача 2. Вероятность всхожести семян пшеницы равна 0,9. Найти вероятность того, что из 400 посеянных семян взойдут 350 семян.

Вычислить искомую вероятность Р₄₀₀(350) по формуле Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим приближенную формулу, выражающую локальную теорему Лапласа:

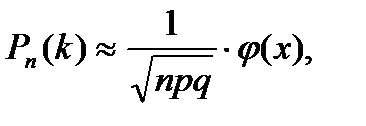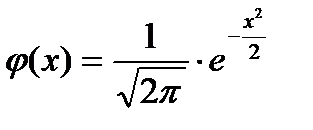где и 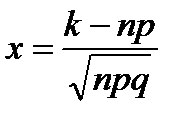.Из условия задачи р=0,9; q=1 — 0,9=0,1; n=400; k=350.

Тогда .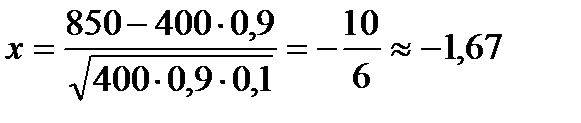

Из таблицы 1 приложений находим 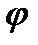( - 1,67) = 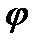(1,67) =О,0989. Искомая вероятность равна:

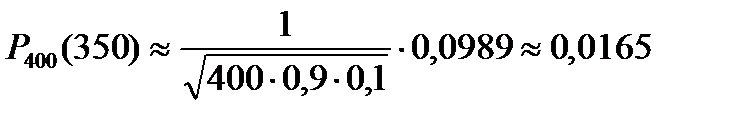
Задача 3. Среди семян пшеницы 0,02% сорняков. Какова вероятность того, что при случайном отборе 10000 семян будет обнаружено 6 семян сорняков?

Применение Локальной теоремы Лапласа из-за малой вероятности р=0,0002 приводит к значительному отклонению вероятности от точного значения P_n(k). Поэтому при малых значениях р для вычисления Р_n(k) применяют асимптотическую формулу Пуассона

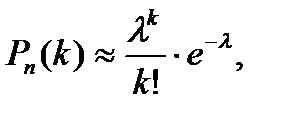где е=2,7182…; 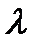=np

Эта формула используется при 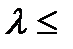10, причем чем меньше р и больше n, тем результат точнее.

По условию задачи р=0,0002; n=10 000; k=6. Тогда 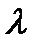=10000*0,0002=2 и

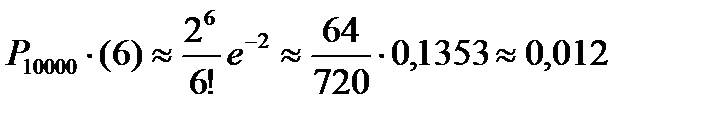
Задача 4. Процент всхожести семян пшеницы равен 90%. Найти вероятность того, что из 500 посеянных семян взойдут от 400 до 440 семян.

Если вероятность наступления события А в каждом из n испытаний постоянна и равна р, то вероятность 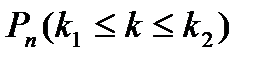того, что событие А в таких испытаниях наступит не менее k₁ раз и не более k₂ раз определяется по интегральной теореме Лапласа следующей формулой:

.

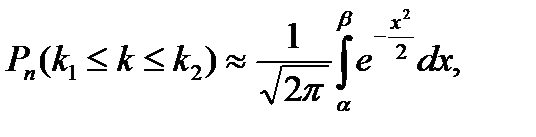
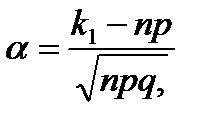
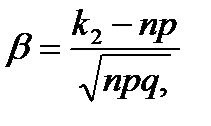Функция Ф(х)= 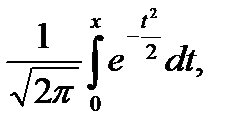называется функцией Лапласа. В приложениях (табл. 2) даны значения этой функции для 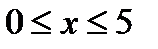. При х>5 функция Ф(х) =0,5. При отрицательных значениях х в силу нечетности функции Лапласа Ф(-х) =-Ф(х). Используя функцию Лапласа, имеем: .

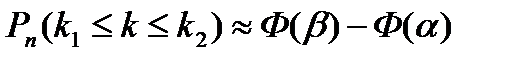По условию задачи n=500; р=0,9; q=0,1; k₁= 400; k₂
=440. По проведенным выше формулам находим 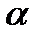и :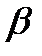

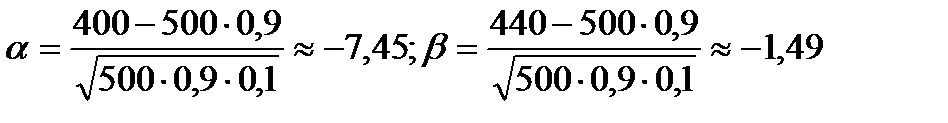
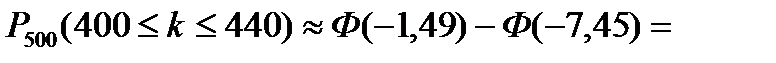
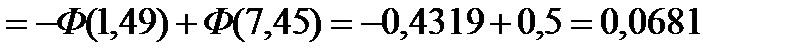
Вопросы для самопроверки

1. Что называется событием? Приведите примеры событий; достоверных событий; невозможных событий.

2. Какие события называются несовместными? совместными? противоположными?

3. Что называется относительной частотой события?

4. Сформулируйте статистическое определение вероятности события.

5. Сформулируйте классическое определение вероятности события..

6. Что называется условной вероятностью события?

7.Сформулируйте теоремы умножения вероятностей для зависимых и независимых событий.

8. Напишите формулу полной вероятности.

9. Как найти наивероятнейшее число наступлений события при повторенных испытаниях?

10. Напишите формулу Бернулли. В каких случаях она применяется?

11. Сформулируйте локальную и интегральную теоремы Лапласа.

12. Напишите формулу Пуассона. В каких случаях она применяется?