Эмпирическим (выборочным) распределением

называется перечень вариант x_iвариационного ряда и их соответствующих частот (или их относительных частот).

При изучении непрерывных распределений, когда значения вариант могут отличаться на сколь угодно малую величину, всю область, где находятся наблюдаемые значения признака, разбиваем на частичные интервалы (a_i-1,a_i,) длиной a_i – a_i-1= h_i и находим для каждого интервала n_i – сумму частот вариант, попавших в этот i-й интервал.

Пример .Дана выборка: 2; 5; 7; 3; 2; 5; 6; 3; 6; 5. Записать выборку в виде вариационного и статистического рядов. Определить объем.

Решение.

Вариационный ряд выборки: 2; 2; 3; 3; 5; 5; 5; 6; 6; 7.

Статистический ряд (дискретный) имеет вид

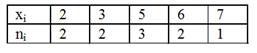
Объем выборки n=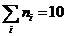

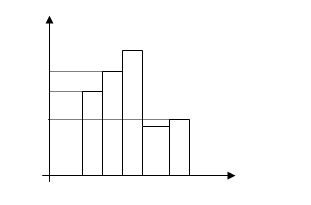
Полигон и гистограмма

Полигоном частот выборки называется ломаная, соединяющая точки (х₁;n₁), (x₂; n₂) ,..., (x_к;n_к).

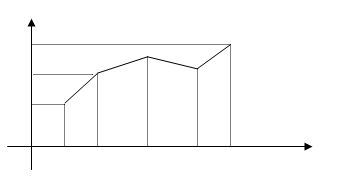
Полигоном относительных частот называется ломаная, соединяющая точки (х₁; W₁), (х₂; W₂),..., (х_к; W_к).

Гистограмма частот– это ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длины h_i, а высоты равны 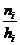(плотность частоты).

Эмпирическая функция распределения

Пусть известно статистическое распределение частот количественного признака ξ, обозначим черезn_x- число наблюдений, при которых наблюдаемое значение признака меньше некоторого числа х.

Эмпирической функцией распределения назовем функцию

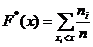
Это есть функция выборочного (эмпиричекого) распределения.

По теореме Бернулли из закона больших чисел следует, что относительная частота события сходится по вероятности к вероятности этого события при ; т. е. при больших n значения F^*(х) и F(x) мало отличаются, т. к.

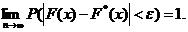
F^*(x) обладает свойствами:

•

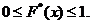
• Неубывающая функция.

• Если х_i=x_min и х_j=х_max соответственно наименьшая и наибольшая варианты ряда, то F^*(x)=0 при х<x_min, и F^*(x)=1 при х>x_max.

• 4Пример:Построить эмпирическую функцию распределения, если распределение выборки имеет вид

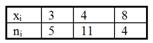
Решение.

Т.к., где n = 20, то

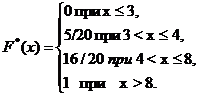
39. Точечные оценки параметров распределения, выборочное среднее, выборочная дисперсия, исправленная дисперсия, метод моментов.

Групповая и общая средние

Допустим, что некоторая совокупность разбита на несколько непересекающихся групп, необязательно одинаковых по объему. Группы называются непересекающимися, если каждый член совокупности принадлежит только одной группе. Рассматривая каждую группу как самостоятельную совокупность, можно найти их среднюю арифметическую.

Групповой средней называют среднее арифмети-ческое значений членов, принадлежащих группе.

Общей средней всей совокупности называют среднее арифметическое значений членов, принадлежащих всей совокупности.

Справедливо предложение:

Общая средняя равна средней арифметической групповых средних всех непересекающихся групп.

Пример. Вычислить среднее число жителей в поселках городского типа по данным таблицы

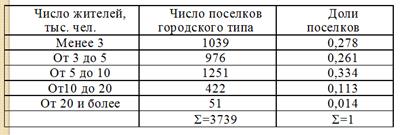
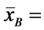(2×1039 + 4×976 +7,5×1251 + 15×422 + 25×51)/3739=6,14 (тыс. чел.)3

Пример .Распределение рабочих предприятия по заработной плате и по цехам приведено в таблице. Найти среднюю зарплату.

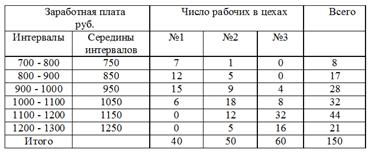
Решение.1 способ

Оценка дисперсии

В качестве оценки D_ξ можно взять распределения выборочную дисперсию

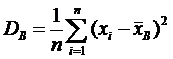
Можно доказать, что выборочная дисперсия является состоятельной и смещенной оценкой генеральной дисперсии D_ξ,причем ,

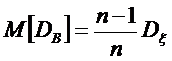
т.е. эта оценка занижает в среднем истинное значение дисперсии на D_ξ /n. Правда это смещение сходит на нет при n ®¥.

С целью исправления смещения вводят несмещенную оценку D_ξ, которой является исправленная выборочная дисперсия

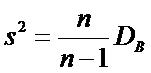
Действительно

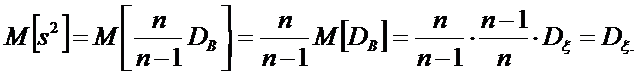
Так как , то оценка s² является несмещенной.

Итак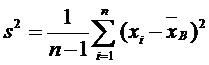

Стандартно вводятся выборочное среднее квадратическое отклонение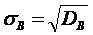

и исправленное среднее квадратическое отклонение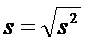

Замечания:

· На практике пользуются исправленной дисперсией, если n£30.

· Если, x_i– варианта выборки, n_i– ее частота и n – объем выборки, то

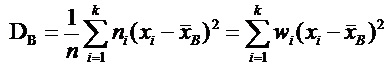
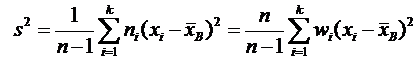
· Для вычисления D_В удобнее применять формулу

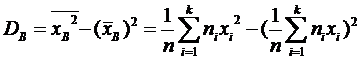
· Выборочное s_в и исправленное s (средние квадратические отклонения) – смещенные оценки s.

· Пример. Из генеральной совокупности извлечена выборка