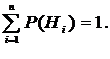Определение условной вероятности. Теорема умножения вероятностей, доказательство в общей формулировке.
Условная вероятность 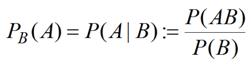
Условная вероятность Р(А|В) события А относительно события В - это вероятность события А при условии, что событие В уже произошло.
Теорема умножения вероятностей. 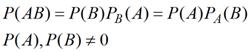
Теорема умножения вероятностей (общая формулировка).
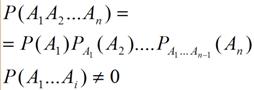
Доказательство
Воспользуемся методом математической индукции.
из определения Р(А1×А2)=Р(А1)×Р(А2|А1).
Предполагаем, что теорема верна для (n-1) событий; докажем, что она верна для n событий.
Найдем Р(А1×А2×А3×...×Аn)=P((A1×A2×A3×...×An-1)×An) = =P(A1×A2×A3×...×An-1)×P(An|A1×A2×A3×...×An-1) = / попредположению /= P(A1)×P(A2|A1)× P(A3|A1×A2) × ..×P(An-1| A1×A2×A3×An-2)×P(An|A1×A2×A3×...×An-1).g
Пример 8:
Два студента выполняют независимо друг от друга задание. Вероятность того, что задание будет выполнено первым студентом 0,6;
для второго студента эта вероятность равна 0,8.
Найти вероятность того, что
· оба студента выполнят задание;
· только один из них выполнит задание;
· хотя бы один из них выполнит задание.
Решение.
События: А – задание выполнит первый студент,
В- задание выполнит второй студент.
По условию Р(А) = р1 = 0,6; Р(В)=р2 = 0,8; следовательно, Р( ) = 1-p1 = q1 = 1-0,6 = 0,4; P( ) = 1-p2 = q2 = 1-0,8 = 0,2.
· Р(А×В) = /события А и В - независимые события / = Р(А)×Р(В) = р1×р2 =0,6×0,8 = 0,48.
·Р(А× + ×B) = / A× и ×B - несовместные события /= Р(А× ) + Р( ×В) = Р(А)×Р( ) +
Р( )×Р(В) = p1×q2+q1×p2 = 0,6×0,2 + 0,4×0,8 = 0,44.
·P(A+B)=/ А и В-совместные события /= Р(А)+Р(В)-Р(А×В)=0,6+0,8-0,48=0,92
или т.к. А+В и противоположные события, то
Р(А+В)=1-Р( )= 1 - Р( )×Р( ) = 1-q1×q2 = 1-0,4×0,2 = 1-0,08 = 0,92.4
Пример 7:
Студент знает ответы на 20 из 25 вопросов. Какова вероятность того, что он ответит на два выбранных наудачу вопроса?
Решение.
Рассмотрим события:
А- студент знает ответ на первый вопрос,
В- студент знает ответ на второй вопрос.
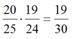 Найдем Р(А×В).
Найдем Р(А×В).
Р(А×В) = Р(А)×Р(В|А) =
|
Теорема (формула полной вероятности)
Пусть в результате опыта может появиться какое-либо из несовместных событий Н1,Н2,...,Нn, образующих полную группу. Событие А может появиться только вместе с одним из этих событий.
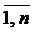 |
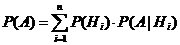 Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А|Нi), где i = , то
Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А|Нi), где i = , то
Доказательство.
Р(А)=Р(А× = =Р(А×(Н1+Н2+...+Нn)=P(A×H1+A×H2+...+A×Hn)=
/события A×Hi иA×Hj, где несовместные события, т.к. (A×Hi)×(A×Hj)=A×Hi×Hj=A×(Hi×Hj)=A×Ø = Ø
= Р(А×Н1)+Р(А×Н2)+...+Р(А×Нn)=
=P(H1)×P(A|H1)+P(H2)×P(A|H2)+...+P(Hn)×P(A|Hn).
Пример:
На стройку поступают блоки с трех баз, причем 50% с первой базы,30% со второй базы, остальные с третьей базы. Вероятность того, что блок c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу на стройке блок окажется бракованным.
Решение.
Рассмотрим гипотезы:
Н1 - взятый наудачу блок поступил с первой базы,
Н2 - взятый наудачу блок поступил со второй базы,
Н3 - взятый наудачу блок поступил с третьей базы.
Событие А - взятый наудачу на стройке блок окажется бракованным.
По условию Р(Н1)=50/100=0,5; Р(Н2)=30/100=0,3; Р(Н3)=(100-50-30)/100 = 0,2.Р(А|Н1)=0,09;
Р(А|Н2)=0,1; Р(А|Н3)=0,08.
Следовательно, по формуле полной вероятности
Р(А)=0,5×0,09+0,3×0,1+0,2×0,08=0,091.
Вопрос 11.
Независимые испытания. Полиномиальная схема.
Производится n независимых испытаний, в каждом из которых события А1, …, Аk наступают с вероятностями р1 ,…, рk (р1 + … + рk= 1).
Найти вероятность P(n1, …, nk) того, что в результате эксперимента событие А1 наступит n1 раз, …, событие Аk наступит nk раз.
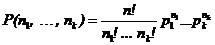 |
Пример. Задача о байдарке.
При прохождении порога байдарка
- не получает повреждений с вероятностью 0,7;
- получает серьезное повреждение с вероятностью 0,2;
- полностью ломается с вероятностью 0,1.
Два серьезных повреждения приводят к поломке. Найти вероятность того, что байдарка преодолеет 10 порогов (т.е. не будет полностью сломана после 10 порогов).
Наивероятнейшее число наступлений события при повторении испытаний:
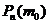 Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события
Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события
по крайней мере не меньше вероятностей других событий при любом m.
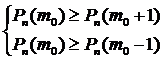
Если m0 – наивероятнейшее число появления события А в n независимых испытаниях, в каждом из которых событие А наступает с постоянной вероятностью р
np-q<m0 <np+p.
Найти наивероятнейшее число отказавших элементов, если каждый из пяти независимо работающих элементов отказывает с вероятностью 0,4.
Решение.
Так как n=5, p=0,4, q=0,6, то 5×0,4-0,6£ m0 <5×0,4+0,4
Или 1,4 < m0 < 2,4. Следовательно, m0=2
8. Теорема (формула Байеса) (теорема переоценки гипотез)
Пусть в условиях предыдущей теоремы (формула полной вероятности) событие А наступило и мы нашли вероятность Р(А). Спросим, как изменились вероятности гипотез в связи с появлением события А, т.е. найдем Р(Нi|А), где i=1,2,...,n.
По аксиоме :Р(А×Нi)=P(A)×P(Hi|A)=P(Hi)×P(A|Hi), откуда
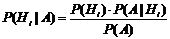
В предыдущем примере событие А наступило, т.е. взятый наудачу на стройке блок оказался бракованным. Определить вероятность того, что этот блок поступил со второй базы.
На стройку поступают блоки с трех баз, причем 50% с первой базы,30% со второй базы, остальные с третьей базы. Вероятность того, что блок c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу на стройке блок окажется бракованным.
Решение.
Рассмотрим гипотезы:
Н1 - взятый наудачу блок поступил с первой базы,
Н2 - взятый наудачу блок поступил со второй базы,
Н3 - взятый наудачу блок поступил с третьей базы.
Событие А - взятый наудачу на стройке блок окажется бракованным.
Решение.
Р(Н2|А) = 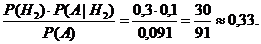

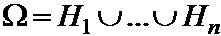
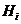 называются гипотезами.
называются гипотезами.