Линейные операторы. Матрица линейного оператора. Действия над линейными операторами. Зависимость между матрицами линейного оператора в различных базисах.

27¹. Линейные операторы.

Оператор (преобразование) 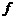линейного пространства V называется линейным оператором (преобразованием), если для любых векторов x и y из V и каждого действительного числа 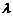выполняются условия:

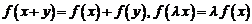. (1)

Для обозначения линейного оператора вместо f часто используется А.

Отметим, что из условий (1) следует, что

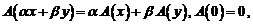(2)

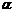где и 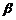– любые действительные числа.

Простейшим примером линейного оператора А является тождественное преобразование, т.е. 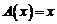, которое каждому вектору 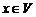ставит в соответствие тот же вектор.

Рассмотрим нетривиальные примеры линейных операторов.

1. Пусть V – n-мерное арифметическое пространство 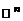и 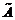– квадратная матрица порядка n. Каждому столбцу 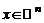поставим
в соответствие вектор-столбец 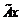. Так определяется оператор .

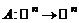На основании определения умножения матриц этот оператор является линейным.

2. Пусть в n-мерном линейном пространстве V линейный оператор А переводит базисные векторы 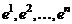соответственно в векторы 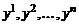, т. е. .

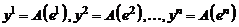Если x – произвольный вектор из этого пространства V, то для 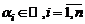, имеем 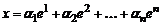. Тогда

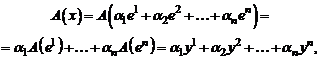
т.е. образ любого вектора 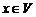можно выразить через образы базисных векторов 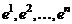. Значит, линейный оператор будет вполне определен, если задать образы базисных векторов данного пространства.

27². Матрица линейного оператора.

Пусть А – линейный оператор, переводящий базис 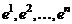соответственно в систему векторов 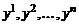. Каждый из векторов последней системы разлагается по базису:

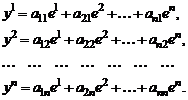
Матрицу

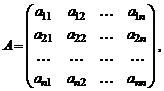(3)

i-тый столбец которой состоит из координат вектора 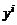, , 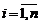называют матрицей линейного оператора А в базисе 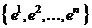и обозначают А (для матрицы оператора сохраним то же обозначение, что и для линейного оператора).

Ранг r этой матрицы называют рангом линейного оператора,
а число 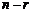– его дефектом.

Таким образом, каждому линейному оператору n-мерного
линейного пространства соответствует матрица порядка n в данном базисе и обратно, каждой матрице порядка n соответствует линейный оператор (преобразование) n-мерного линейного пространства.

В частности, матрица А тождественного преобразования в любом базисе n-мерного линейного пространства будет единичной порядка n; любой единичной матрице порядка n соответствует тождественное преобразование n-мерного линейного пространства.

27³. Действия над линейными операторами.

Каждая квадратная матрица порядка n задает некоторый оператор А n-мерного линейного пространства V и наоборот.

Это обстоятельство позволяет на множестве линейных операторов определить операции, аналогичные операциям на множестве матриц.

Пусть 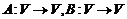– два линейных оператора. Суммой операторов А и В называют линейный оператор 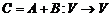, который каждому вектору 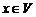ставит в соответствие вектор 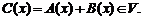Если в пространстве V задан базис, то матрица оператора С в заданном базисе равна сумме матриц операторов А и В
в этом базисе.

Произведением линейного оператора 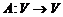на число 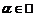называют оператор 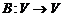, который каждому вектору 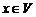ставит в соответствие вектор 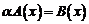. Матрица оператора 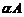в заданном базисе равна произведению матрицы оператора А на число .

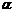Результат последовательного использования двух линейных операторов 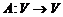, 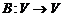называют их произведением и обозначают 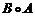(оператор, который выполняется первым, записывают с правой стороны), т.е. 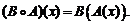Если в пространстве V задать базис и обозначить через А матрицу оператора А, а через В матрицу оператора В в этом базисе, то матрица оператора 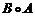в том же базисе равна произведению матриц В и А.

Произведение операторов чаще называют композицией или суперпозицией.

27⁴. Зависимость между матрицами линейного оператора в различных базисах.

Пусть в 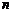-мерном линейном пространстве 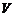заданы два базиса 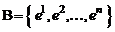и 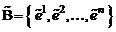; первый из них назовем старым, а второй – новым. Обозначим через 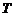линейное преобразование, переводящее базис 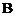в .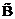

Утверждение 1. Если 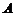– матрица линейного преобразования
в старом базисе 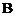, то матрица 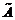этого преобразования в новом базисе 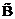имеет вид .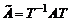