Языковые свойствах числовых систем.

В предыдущих пунктах 1.1 – 1.6 построены три числовые знаковые системы:

- система натуральных чисел N, предназначенная для реализации интеллектуальной функции перечисления объектов;

- система рациональных чисел Q , в которой реализуются арифметические операции;

- система действительных чисел R , которая даёт возможность как измерять протяжённости, так и реализовывать арифметические операции.

Напомним, что согласно определению Л. Эйлера знаковая система образует язык, если позволяет реализовать следующие три интеллектуальные функции. Сформировать образ – реализация опорной функции; построить умозаключение или, что то же, отследить смысл – логическая функция; реализовать эти две функции в виде высказывания – коммуникационная функция.

Несложно убедиться в том, что все три упомянутые числовые системы позволяют реализовать указанные функции. Поэтому можно заключить, что натуральный ряд – это язык счёта, рациональные числа – язык арифметики и, наконец, действительные числа – это язык измерений и арифметики одновременно.

Отметим некоторые свойства этих языковых систем.

1. Свойство оптимизации интеллектуальной деятельности. Действительно, эти языки построены с целью оптимизации интеллектуальных функций счёта, вычислений и измерений.

2.Язык натуральных чисел является простейшим среди всех языковых систем. Это следует из того, что любой язык среди прочих интеллектуальных функций реализует и функцию перечисления объектов. Язык натурального ряда реализует только функцию перечисления.

Рассматривая задачу измерения отрезков прямой действительными числами, мы установили взаимно-однозначное соответствие между множеством точек прямой и множеством действительных чисел в десятичном представлении. Это позволяет визуализировать арифметические операции, изображая результаты сложения, вычитания и деления отрезков прямой. Так, например, сумму двух действительных чисел p + 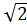можно вычислить с любой степенью точности в десятичной системе, а можно и изобразить как суммарный отрезок, используя построения в задачах 1 и 2 из п.1.4. При этом результат суммы в одной из этих реализаций будет соответствовать результату суммы в другой реализации. То же можно сказать и об операциях вычитания, умножения и деления.

Взаимно-однозначное соответствие между множествами, которое сохраняет результат операций на этих множествах называется изоморфизмом.

Учитывая это понятие изоморфизма, мы устанавливаем следующее свойство.

Десятичная (и вообще, любая k-ичная) знаковая реализация действительных чисел изоморфна геометрической реализации действительных чисел в виде отрезков прямой.

Это свойство является простейшей демонстрацией удивительной способности человеческого интеллекта представлять свои чувства в числовом формате.

1.8 Вопросы и задания к теме «числовые системы».

Вопросы.

1. Какую роль играет аксиома индукции в аксиоматике натурального ряда Д. Пеано?

2. Объясните, почему языка рациональных чисел не достаточно для реализации процессов измерения отрезков?

3. Какую роль играет аксиома Архимеда в аксиоматике рациональных чисел?

4. Какие интеллектуальные задачи реализуют языки натуральных, рациональных и действительных чисел?

5. Какую роль играет аксиома о вложенных промежутках в аксиоматике действительных чисел и как строится взаимно-однозначное соответствие между действительными числами и точками евклидовой прямой?

6. Используется ли в практической деятельности человека полная модель действительных чисел, или для практических нужд достаточно рациональных чисел? Почему?

Задания.

1. Покажите, что системы натуральных, рациональных и действительных чисел независимо от выбора знаковой реализации являются языковыми системами в смысле Л. Эйлера.

2. Как можно представить «слова» и «предложения » в языке рациональных чисел, действительных чисел? Приведите пример текстового формата в этих языках.

3. Постройте изоморфизм между реализацией действительных чисел в десятичной системе и геометрической реализацией в виде отрезков евклидовой прямой.

( Указание: задать единичный отрезок на евклидовой прямой, а операции умножения и деления определить как порции этого отрезка; использовать алгоритм построения рациональных чисел циркулем и линейкой на евклидовой прямой.)

4. Покажите, что реализации действительных чисел в виде k-ичных систем изоморфны для различных k = 2, 3, …, n.

5. Как связаны аксиома Кантора «о вложенных отрезках» на евклидовой прямой и аксиома о вложенных промежутках в аксиоматике действительных чисел?