ДУ, допускающие понижение порядка (2 случая)

1) ДУ вида 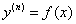(1)

Для решения ДУ (1) надо проинтегрировать уравнение n-раз

2) ДУ вида y’’=f (x, y’) ( то есть правая сторона не зависит от у)

Полагаем, y’=p, p=p(x) –неизвестная функция. Следовательно, y’’’=p’

Подставим y’, y’’ в уравнение: p’=f(x,p), то есть ДУ первого порядка

10. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
ЛОДУ 2-го порядка с постоянными коэффициентами называется уравнение вида:

y’’+py’+qy=0 (1), гдеp,q –заданные числа

Теорема (структура общего решения ЛОДУ): Пусть 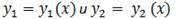- линейно независимые частные решения уравнения (1), тогда 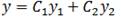-общее решение уравнения(1), где 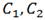-произвольные постоянные

Рассмотрим: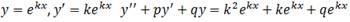

Полагаем => =>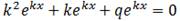

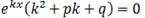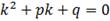
Следовательно, 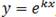является решением уравнения (1), если 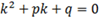(2) – характеристическое уравнение

Возможны три случая:

1) D>0 => 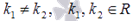. Тогда из теоремы следует 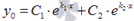- общее решение

2) D=0 =>k1=k2 – действительные корни уравнения (2). Тогда 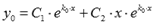- общее решения (1)

3) D<0 => 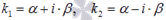- комплексносопряженные корни. Тогда,

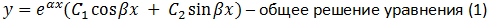
Линейные неоднородные ДУ 2-го порядка с постоянными коэффициентами.

ЛНДУ 2-го порядка с постоянными коэффициентами называется уравнение вида 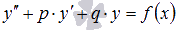, где

p, q – заданные действительные числа

f(x) – заданная функция

Определение двойного интеграла, его свойства

Если существует конечный предел интегральной суммы 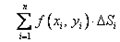при n–> 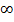, не зависящий от способа разбиения i области D и выбора точек (x_i,y_i), то этот предел называют двойным интегралом от функции f(x, y) по области D.

Обозначение:
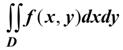, т.е.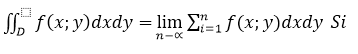

Свойства: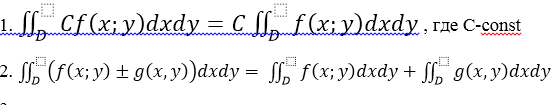

3.

Пусть D=D1∪D2(объединение), D1 ⋂D2 – линия

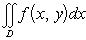
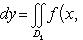
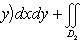
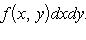
Тогда

13. Вычисление двойного интеграла
Обознач.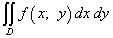
Опр.Если существует конечный предел сумма
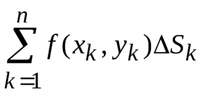(ВМЕСТО k БУКВА i)при n ∞, независимо от способа разбиения области D и выбора точек (x_i,y_i), то предел называеют двойным интегралом от функции f(x,y) по области D.

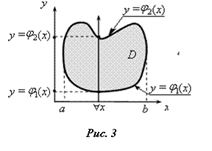
Область первого типа( область правильная относительно оси ОY)

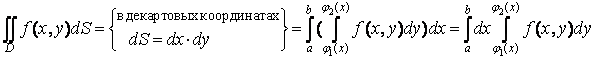
Область второго типа( область правильная относительно оси OX)

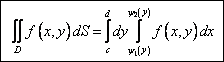
Формула перехода к полярным координатам

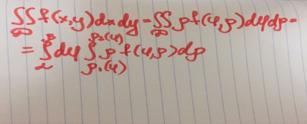
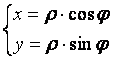
К полярным координатам рекомендуется переходить, если1) подынтегральная функция зависит от x²+ y², т.е f(x²+y²) в область D входит окружность или ее часть.

14.Приложения двойного интеграла
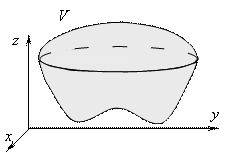
Замечание: Цилиндрическое тело- тело, ограниченное сверху - поверхность z=f(x,y) снизу – областью D с боков – поверхностью с образующей пар. Оси OZ

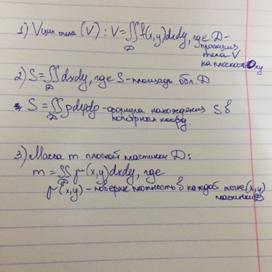
Определение тройного интеграла и его свойства.

Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):

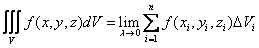
здесь n – это количество элементарных частей разбиения области V;
P_i (x_i,y_i,z_i) – произвольно выбранная точка на каждой элементарной части,

i = 1,...,n;

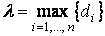— ранг разбиения;
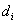– диаметр i-ой элементарной части.