А. Классическое определение вероятности. Теоремы сложения и произведения вероятностей.
ЗАДАЧИ К ЭКЗАМЕНУ
ФЭУБ, 2 КУРС 3 СЕМЕСТР
1. ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1) Дано статистическое распределение выборки: в первой строке указаны выборочные варианты хi , а во второй строке – соответственные частоты ni количественного признака Х). Требуется найти:
1. Методом произведений: а) выборочную среднюю; б) выборочное среднее квадратическое отклонение;
2. Доверительные интервалы для оценки неизвестного математического ожидания а с заданной надежностью g=0,95.
3. Пользуясь критерием Пирсона, при уровне значимости a=0,05, установить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с данными выборки объема n=100:
1.1)
| хi | |||||||
| ni |
1.2)
| хi | 10,6 | 15,6 | 20,6 | 25,6 | 30,6 | 35,6 | 40,6 |
| ni |
1.3)
| хi | |||||||
| ni |
1.4)
| хi | 12,4 | 16,4 | 20,4 | 24,4 | 28,4 | 32,4 | 36,4 |
| ni |
1.5)
| хi | |||||||
| ni |
1.6)
| хi | |||||||
| ni |
1.7)
| хi | 10,2 | 10,9 | 11,6 | 12,3 | 13,7 | 14,4 | |
| ni |
1.8)
| хi | 11,5 | 12,5 | 13,5 | 14,5 | |||
| ni |
1.9)
| хi | |||||||
| ni |
1.10)
| хi | |||||||
| ni |
1.11)
| хi | 12,5 | 13,5 | 14,5 | 15,5 | |||
| ni |
1.12)
| хi | |||||||
| ni |
2. Найти по данной корреляционной таблице:
а) выборочное уравнение прямой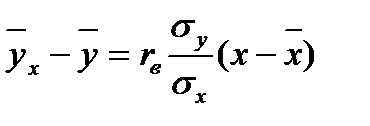 
регрессии Y на Х;
б) выборочное корреляционное отношение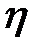 
YX
2.1)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.2)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.3)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.4)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.5)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.6)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.7)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.8)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.9)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
2.10)
| Y | X | ny | |||||
| -3 | -2 | -1 | |||||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
ЗАДАЧИ К ЭКЗАМЕНУ
ФЭУБ, 2 КУРС 3 СЕМЕСТР
1. ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ.
А. Классическое определение вероятности. Теоремы сложения и произведения вероятностей.
1) В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.
2) В лифт на первом этаже девяти этажного дома вошли 4 человека, каждый из которых может выйти независимо друг от друга на любом этаже. Какова вероятность, что все пассажиры выйдут на одном этаже?
3) По условиям лотереи «Спортлото 6 из 45» Участник лотереи, угадавший 4, 5, 6 видов спорта из отобранных при случайном розыгрыше 6 видов спорта из 45, получает денежный приз. Найти вероятность: а) того, что будут угаданы 4 цифры; б) того, что будет получен денежный приз.
4) В магазине было продано 21 из 25 холодильников трех марок, имеющихся в количествах 5, 7 и 13 штук. Полагая, что вероятность быть проданным для холодильника каждой марки одна и та же, найти вероятность того, что остались не распроданными холодильники одной марки.
5) Перед окопами вдоль прямой линии через каждые 10м установлены противотанковые мины. Перпендикулярно этой линии движется танк, ширина которого 3м. Какова вероятность того, что танк пересечёт линию установки мин невредимым, т.е. что мина не взорвётся?
6) Два лица А и В условились встретиться в определённом месте, договорившись только о том, что каждый является туда в любой момент времени между 11 и 12ч и ждёт в течении30 мин. Если партнёр к этому времени ещё не пришел или уже ушел, встреча не состоится. Какова вероятность того, что встреча состоится?
7) Среди одинаковых по внешнему виду 11 изделий находятся три бракованных. Произвольно вынимают три изделия. Какова вероятность, что среди них хотя бы одно бракованное?
8) Работа электронного устройства прекратилась в результате выхода из строя одного из 5 унифицированных блоков. Производится последовательная замена каждого блока новым до тех пор, пока устройство не начнёт работать. Какова вероятность того, что придётся заменить 2 блока.
9) На 100 лотерейных билетов приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному билету, если приобретено 2 билета?
10) Устройство содержит два независимо работающих элемента, вероятности отказа которых за время Т соответственно равны 0,4 и 0,3. Найдите вероятность того, что за время Т откажет только один элемент.
11) Вероятность того, что сброшенная с самолета бомба попадет в цель, равна 0,03. вероятность того, что бомба разорвется, равна 0,99. Найти вероятность того, что цель будет уничтожена одной сброшенной бомбой.
12) Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наудачу взятое изделие стандартно, равна 0,7. Найдите вероятность того, что из двух проверенных изделий только одно окажется стандартным.
13) Баскетболист бросает мяч в корзину до первого попадания. Вероятность попадания при каждом броске равна 0,6. Какова вероятность того, что баскетболист попадет в корзину только с третьего раза?
14) В технической библиотеке имеются 70 книг по технике и 30 книг по математике. Зашедший в библиотеку читатель заказывает 3 книги. Какова вероятность того, что все они по одной тематике?
15) Два стрелка произвели по одному выстрелу по мишени. Вероятность того, что первый стрелок попал в цель, равна 0,7; для второго стрелка эта вероятность равна 0,8. Найти вероятность того, что хотя бы один из двух стрелков попал в цель.
16) Из слов «мама» и «дама» наугад выбирают по одной букве. Какова вероятность совпадения этих букв?
17) На колышек набрасывают кольца до первого попадания. Вероятность попадания при каждом броске равна 0,7. Какова вероятность, что будет израсходовано 4 кольца?
18) Студент пришел на экзамен, выучив лишь 20 вопросов из 25, имеющихся в программе. Преподаватель задает ему 4 вопроса. Какова вероятность, что студент знает более двух вопросов?
19) Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что из 5 выстрелов будет ровно 3 попадания.
20) Завод выпускает электролампочки. Среди изготовленных лампочек в среднем 4.5% неисправных. Найти вероятность того, что среди 25 наудачу выбранных лампочек окажется 20% неисправных. Найдите наивероятнейшее число неисправных электролампочек в указанной выборке и какова его вероятность?
21) Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0.015. Найти вероятность того, что среди 20 случайно отобранных деталей окажется одна бракованная. Каково наивероятнейшее число бракованных деталей в выборке из 20 деталей и какова его вероятность?
22) Среди производимых заводом стиральных машин 99% не имеют никаких дефектов. Найдите вероятность того, что из 38 машин, завезенных в магазин, окажется менее 3 дефектных. Определите наивероятнейшее число машин (и его вероятность) среди завезенных в магазин, имеющих дефект.
23) Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин купил по одной акции шести АО. Какова вероятность того, что среди купленных акций 2 окажутся акциями банкротов?
24) Из 15 лотерейных билетов выигрышными являются 4. Какова вероятность того, что среди 6 билетов, взятых наудачу, будет 2 выигрышных?
25) Средний процент нарушений в работе телевизоров определенной марки в течение гарантийного срока равен 12. Вычислите вероятность того, что из 26 проданных телевизоров не менее 23 выдержат гарантийный срок. Найдите наивероятнейшее число (и его вероятность) проданных телевизоров, которые выдержат гарантийный срок.
26) Из 100 изготовленных деталей 10 имеют дефект. Для проверки были отобраны 5 деталей. Какова вероятность того, что среди отобранных деталей 2 окажутся бракованными?
27) Вероятность наступления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что в 100 испытаниях событие появится не менее 75 и не более 85 раз.
28) Студент знает 40 из 60 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете.
29) Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно р1 = 0,4; р2 = 0,5; р3 = 0,7. Найти вероятность того, что в результате этих трех выстрелов в мишени будет: 1) ровно одна пробоина; 2) хотя бы одна пробоина.
30) Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна семи.
31) Монета брошена два раза. Найти вероятность того, что хотя бы один раз выпадет «орел».
32) В коробке содержатся 6 одинаковых, занумерованных кубиков. Наугад по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
33) В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.
34) Среди деталей, обрабатываемых рабочим, бывает в среднем 4 % нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными. Каково наивероятнейшее число нестандартных деталей в рассматриваемой выборке из 30 деталей и какова его вероятность?
35) Вероятность попадания в цель при одном выстреле равна 0,8. найти вероятность того, что в серии из четырех выстрелов будет: а) хотя бы одно попадание; б) не менее трех попадании; в) не более одного попадания.
36) Вероятность того, что необходимый студенту учебник имеется в библиотеке, равна 0,3. Найти вероятность того, что студент не найдет необходимый ему учебник ни в одной из трех центральных библиотек города.
37) На склад поступили 3 партии телевизоров от разных производителей. Для проверки на качество отбирается по одному телевизору из каждой партии. Вероятность брака в партии телевизоров фирмы А равна 0,09, фирмы В – 0,02, фирмы С - 0,1. Найти вероятность того, что все отобранные для контроля телевизоры будут бракованными.
38) На экзамен по математике вынесено три темы. В билете содержится 3 вопроса: по одному из каждой темы. Вероятность того, что студент ответит на вопрос темы №1, равна 0,9, на вопрос темы №2 – 0,8, темы №3 – 0,95. Найти вероятность того, студент ответит на все вопросы в билете.
39) Три стрелка стреляют по цели и делают по одному выстрелу. Вероятность попадания в цель первым стрелком равна 0,7, вторым – 0,8, третьим – 0,9. Найти вероятность того, что все стрелки поразят цель.
40) Вероятность того, что пассажир опоздает на транзитный автобус, равна 0,01. Найти вероятность того, что на этот рейс опоздают три пассажира из пяти купивших бмлет.
41) Вероятность того, что на малом предприятии вакантно место инженера, равна 0,1. Найти вероятность того, что на трех предприятиях из четырех, заинтересовавших выпускников КубГТУ, вакантно место инженера.
42) Вероятность того, что в течение гарантийного срока холодильник данной фирмы выйдет из строя, равна 0,05. Найти вероятность того, что в течении гарантийного срока выйдут из строя три из четырех холодильников, приобретенных для школы-интерната.
43) Вероятность того, что в букинистическом магазине имеется интересующая читателя книга, равна 0,2. Найти вероятность того, что читатель не найдет данную книгу ни в одном из трех известных ему букинистических магазинов.
44) Вероятность того, что вакцина предотвратит у пациента заболевание гриппом, равна 0,9. Найти вероятность того, что три из пяти пациентов, прошедших вакцинацию, не заболеют гриппом.
45) Вероятность того, что лотерейный билет окажется выигрышным, равна 0,3. Найти вероятность того, что все три купленные гражданином билета, окажутся выигрышными.