Десятичная запись дробных чисел. Правила
| Дроби со знаменателями 10, 100, 1000, 10 000 и т. д. принято записывать без знаменателя. Например: = 0,3 ; = 0,07 ; 2 = 2,86 ; 25 = 25,034 . ), ), ) и т. д. | ||||||||||||||
| Разберем пример десятичной дроби 23,71. Так как перед запятой стоит 23, значит в этой десятичной дроби двадцать три целых, после запятой 71, значит числитель дробной части 71. После запятой записано два символа, значит, знаменатель единица с двумя нулями, то есть сотня. Читаем: " Двадцать три целых семьдесят одна сотая (23 ) ". ) ". |
Сравнение десятичных дробей. Правила
| Важно знать, что дробь 0,3 и дробь 0,30 равны друг другу. Нули, приписанные в конце десятичной дроби, не меняют ее величины, и на координатном луче они будут располагаться в одной точке. | ||||||||
| При сравнении десятичных дробей в первую очередь сравниваем целые части (расположены слева от запятой). Например: 7,56 > 2,97 так как 7 > 2 . Если целые части равны тогда сравниваем дробные части 2,55 > 2,43 потому что > . > . | ||||||||
Как и натуральные числа, меньшие десятичные дроби на координатном луче лежат левее, чем большие. 0,3 < 0,6  |
Сложение и вычитание десятичных дробей. Правила
| Возьмем две десятичные дроби 22,25 и 17,7 и сложим их, приписав к17,7 один нуль ( 17,70 ). 22,25 + 17,70 = 22 + 17 = 22 + 17 +
= 39 = 39,95 | ||||||||
 Таким же образом находится разность десятичных дробей. Мы можем представить их в виде смешанных чисел либо найти разность столбиком. 75,36 – 29,201 = 75,360 – 29,201 = 75 – 29 =
) = 46 = 46,159 | ||||||||
| При сложении (вычитании) десятичных дробей надо: 1) при необходимости уравнять количество знаков после запятой, добавляя нули к соответствующей дроби. 2) Записать дроби так, чтобы их запятые находились друг под другом. 3) Сложить (вычесть), не обращая внимания на запятую. 4) Поставить запятую в сумме (разности) под запятыми, складываемых (вычитаемых) дробей. |
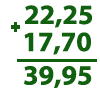Ответ будет таким же, если мы сложим эти десятичные