Прямая линия в пространстве. Различные виды уравнений прямой.

а) Прямая линия как пересечение плоскостей. Прямую линию в пространстве будем рассматривать как пересечение двух плоскостей. Обозначим через 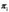и какие-нибудь две различные плоскости, пересекающиеся по прямой 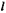. Уравнение 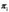и 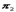известны:

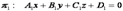
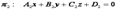
Так как прямая 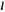представляет собой пересечение плоскостей 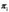и , то она определяется совместным заданием двух уравнений:

.

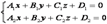Б) Каноническое уравнение прямой.

Пусть дана какая-нибудь прямая. Каждый не равный нулю вектор, лежащий на этой прямой или параллельный ей, называется направляющим вектором этой прямой. Будем его обозначать .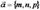

Выведем уравнение прямой, проходящей через данную точку 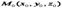и имеющей данный направляющий вектор .

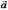Пусть 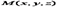- произвольная точка прямой. Вектор 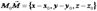коллинеарен направляющему 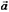, следовательно, справедливы формулы:

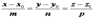(2)

Уравнение (2) называется каноническим уравнением прямой.

В) Параметрические уравнения прямой.

Пусть дано каноническое уравнение прямой. Обозначим буквой 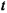каждое из равных соотношений, которые учувствуют в этом уравнении.

,

Тогда 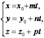(3)

(3) – параметрическое уравнение прямой, проходящей через точку 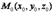в направлении вектора 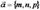. Здесь 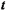рассматривается как произвольно изменяющийся параметр, 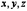- как функции от .

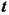Угол между двумя прямыми в пространстве.

Условия параллельности и перпендикулярности прямых. Взаимное расположение прямых в пространстве.

За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.

Один из этих углов равен углу между направляющими векторами этих прямых.

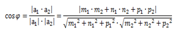
Где первая прямая задается:

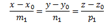
а₁=( m₁, n₁, p₁)

Вторая прямая задается:

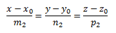
а₂=( m₂, n₂, p₂)

Если прямые параллельны, то

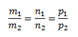
Если прямые перпендикулярны, то m₁ m₂+ n₁ n₂ + p₁ p₂=0.

Взаимное расположение прямых в пространстве

Существует три варианта взаимного расположения двух прямых в пространстве: прямые могут быть пересекающимися, параллельными и скрещивающимися.

Пересекающиеся прямые

Две различные прямые называются пересекающимися, если они имеют общую точку. Точка пересечения единственна: если две прямые имеют две общие точки, то они совпадают.

Параллельные прямые

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые

Если две прямые пересекаются или параллельны, то, как мы видели, через них можно провести плоскость (и притом единственную). Возможна также ситуация, когда через две прямые плоскость провести нельзя.

Определение. Две прямые называются скрещивающимися, если они не параллельны и не пересекаются.

Равносильное определение такое: две прямые называются скрещивающимися, если они не лежат в одной плоскости