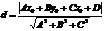Общее уравнение прямой на плоскости

Рассмотрим на плоскости Оху произвольную прямую L. Пусть дана некоторая ее точка М1(х1у1) и вектор N=Ai+Bj, перпендикулярный рассматриваемой прямой. Этот вектор называется нормальным вектором прямой. Точка М1 и нормальный вектор N вполне определяют положение прямой L на плоскости Оху.

Пусть М(х,у) - любая точка прямой L (она называется текущей точкой). По условию, вектор N перпендикулярен вектору , лежащему на этой прямой. Поэтому скалярное произведение (N, )=0, или в координатной форме А(х – х1) + В(у – у1) = 0

Произведем преобразования – раскроем скобки:

АX + ВY + [-АX1 – ВY1 ] = 0

В квадратных скобках у нас некое число. так как А и В числовые коэффициенты, а х1 и у1 - координаты точки и, если это число обозначим С, то получится общее уравнение прямой на плоскости.

АX + ВY + С = 0

Угол между прямыми на плоскости. Взаимное расположение двух прямых на плоскости.

Пол углом между этими прямыми понимают угол между направляющими векторами S₁ и S₂.

Для нахождения острого угла между прямыми L₁ и L₂ числитель правой части формулы следует взять по модулю.

Если прямые L₁ и L₂ перпендикулярны, то в этом и только в этом случае имеем cos =0. следовательно, числитель дроби = 0, т.е. =0.

Если прямые L₁ и L₂ параллельны, то параллельны их направляющие векторы S₁ и S₂. следовательно, координаты этих векторов пропорциональны: .

Условие, при котором две прямые лежат в одной плоскости:

=0.

При выполнении этого условия прямые либо лежат в одной плоскости, то есть либо пересекаются.

Расстояние от точки до прямой.

Расстояние d от точки M0(x0,y0,z0)до прямой Аx+By+C=0 вычисляется по формуле:

Расстояние от точки до прямой есть всегда величина положительная.

Уравнение линии в пространстве.

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

F(x, y, z) = 0.

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.

Тогда пару уравнений назовем уравнением линии в пространстве.

Плоскость в пространстве.

Простейшей поверхностью является плоскость. Плоскость в пространстве можно задавать различными способами. Каждому из них соответствует определенный вид ее уравнения.

Общее уравнение плоскости.

В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение

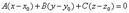
определяет плоскость, проходящую через точку 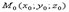и имеющей нормальный вектор .

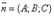Раскрывая в уравнении (1) скобки и обозначая число 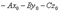буквой D, представим его в виде

.

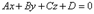Это уравнение называется общим уравнением плоскости.

Угол между двумя плоскостями:

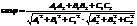
Условие параллельности прямых заключается в равенстве их угловых коэффициентов.

tgφ1=tgφ2 или k1=k2

Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1

k1*k2=-1

Расстояние от точки до плоскости: