Методы построения эпюр в статически определимых и статически неопределимых системах

МЕТОДЫ ПОСТРОЕНИЯ ЭПЮР В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ

Введение

Эта книга в значительной степени соответствует курсу лекций, на протяжении многих лет читаемых в Санкт-Петербургском государственном университете для студентов строительной специальности.

Книга состоит из четырех глав, в которых достаточно подробно рассматриваются методы построения эпюр внутренних силовых факторов статически определимых и статически неопределимых стержневых системах.

В большинстве изданных учебников и учебных пособий по строительной механике этот важнейший вопрос излагается поверхностно, или вообще отсутствует.

В главе 1 рассматривается построение эпюр в различных стержневых системах: балках, рамах, плоскопространственных и др.

В главе 2 приводятся различные общие методы определения перемещений, что имеет самостоятельное значение, а также является базой для двух последующих глав.

В главе 3 дается подробное изложение метода сил применительно к расчету статически неопределимых балок и рам. Рассмотрены все проверки метода, а также использование симметрии.

Глава 4 посвящена изложению метода перемещений. Приведенный здесь материал в лекционном курсе, как правило, не излагается в связи с ограниченностью во времени. Тем не менее метод перемещений очень важен, так как, во-первых, является мощным инструментом для расчета статически неопределимых систем, а во-вторых, используется студентами в дисциплинах, читаемых на старших курсах.

Книга снабжена большим количеством примеров.

Глава 1

Построение эпюр внутренних силовых факторов

Виды сопротивлений

В зависимости от характера внешней нагрузки и от особенностей нагружаемого тела, в поперечных сечениях могут возникать не все шесть внутренних силовых факторов, а какой-либо один или некоторая их комбинация. В соответствии с этим различают следующие виды сопротивлений.

Растяжение (или сжатие) - это вид сопротивления, при котором во всех поперечных сечениях возникает только продольная сила .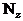

Кручение - это вид сопротивления, при котором во всех поперечных сечениях возникает только крутящий момент .

Чистый изгиб - это вид сопротивления, при котором во всех поперечных сечениях возникает только изгибающий момент 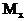(или ). Чаще всего изгибающий момент 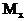сопровождается наличием поперечной силы (или момент сопровождается наличием поперечной силы ). В этом случае имеет место поперечный изгиб.

Возможны случаи, когда в поперечных сечениях возникают два и более внутренних силовых фактора одновременно (исключая их комбинации, рассмотренные выше), тогда говорят о сложном сопротивлении..

Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. При формировании расчетной схемы все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.3,а), шарнирно-неподвижная опора (рис.3,б) и жесткое защемление, или заделка (рис.3,в).

Рис. 3

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.

В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.

В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.

При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.

1.4 Построение эпюр продольных сил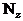

Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.

Правило знаков для 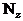: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной - в противном случае.

Пример 1. Построить эпюру продольных сил для жестко защемленной балки (рис.4).

Порядок расчета:

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.

2. Определяем продольную силу 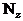в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

3. По найденным значениям строим эпюру .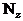

Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.

Рис. 4

1.4 Построение эпюр крутящих моментов

Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.

Правило знаков для : условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным - в противном случае.

Пример 2. Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5,а).

Порядок расчета.

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1.Намечаем характерные сечения.

2.Определяем крутящий момент в каждом характерном сечении.

3.По найденным значениям строим эпюру (рис.5,б).

Рис. 5

1.6 Правила контроля эпюр 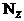и

Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

1. Эпюры 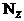и всегда прямолинейные.

2. На участке, где нет распределенной нагрузки, эпюра 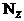( ) - прямая, параллельная оси; а на участке под распределенной нагрузкой - наклонная прямая.

3. Под точкой приложения сосредоточенной силы на эпюре 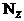обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре будет скачок на величину этого момента.

1.7 Построение эпюр поперечных сил и изгибающих моментов в балках

Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора - поперечная сила и изгибающий момент .

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Правило знаков для : условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде

Изгибающий момент в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для : условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде:

Следует отметить, что при использовании правила знаков для в указанном виде, эпюра всегда оказывается построенной со стороны сжатых волокон балки.

Консольные балки

При построении эпюр и в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3. Построить эпюры и (рис.6).

Рис. 6

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечную силу в каждом характерном сечении.

По вычисленным значениям строим эпюру .

3. Определяем изгибающий момент в каждом характерном сечении.

По вычисленным значениям строим эпюру , причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

1.9 Дифференциальные зависимости между

Указанные зависимости используются при построении эпюр , поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.

Пример 4. Построить эпюры (рис.7).

В данном случае для правильного построения эпюры необходимо использовать приведенные выше дифференциальные зависимости.

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечные силы в характерных сечениях.

Строим эпюру .

Характер эпюры, то есть тот факт, что эпюра пересекает ось, говорит о том, что в этом сечении момент будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.

Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки q:

Рис. 7

Определяем изгибающие моменты в характерных сечениях.

4. Вычисляем экстремальное значение изгибающего момента в сечении, где :

Строим эпюру .

Балки на двух опорах

В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:

Условие используется для проверки вычисленных значений опорных реакций.

Пример 5.Построить эпюры для балки с шарнирным опиранием (рис.8).

Порядок расчета.

1. Вычисляем реакции опор.

Проверка:

2. Намечаем характерные сечения.

В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.

3. Определяем поперечные силы в характерных сечениях.

Строим эпюру .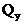

4. Определяем изгибающие моменты в характерных сечениях.

Рис. 8

Строим эпюру

Пример 6. Построить эпюры 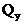и для балки на двух опорах с консолью (рис.9,а)

Порядок расчета.

1. Вычисляем опорные реакции.

Во втором уравнении равновесия (впрочем, как и в первом) момент от распределенной нагрузки 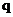вычислен без разбиения ее на две части - слева и справа от опоры В, то есть определена равнодействующая нагрузки 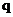- 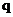×3, ее положение (в середине участка с распределенной нагрузкой), что позволяет определить плечо равнодействующей относительно опоры В и направление создаваемого ею момента. В то же время можно было в уравнении равновесия учитывать отдельно части нагрузки 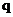, приложенные слева и справа от опоры В; при этом второе уравнение равновесия имеет вид:

Рис.9

Вычисленное из этого уравнения значение реакции 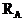, разумеется, совпадает с полученным ранее.

Проверка:

2. Намечаем характерные сечения.

3. Вычисляем поперечную силу и изгибающий момент в характерных сечениях.

Из рассмотрения левой отсеченной части:

Для сечений 5-7 удобнее рассматривать правую отсеченную часть:

По вычисленным значениям строим эпюры 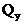и (рис.9,б,в).

1.11 Правила контроля эпюр Q_у и M_x

Дифференциальные зависимости между определяют ряд закономерностей, которым подчиняются эпюры 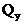и .

1. Эпюра 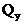является прямолинейной на всех участках; эпюра - криволинейная (квадратная парабола) на участке под равномерно распределенной нагрузкой, причем, выпуклость кривой всегда обращена навстречу нагрузке 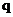, и прямолинейная на всех остальных участках.

2. Под точкой приложения сосредоточенной силы (реакции) на эпюре 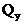обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре 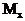обязателен скачок на величину момента.

3. Если на участке под распределенной нагрузкой эпюра 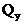пересекает ось , то эпюра 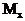в этом сечении имеет экстремум.

4. На участках с поперечной силой одного знака эпюра 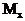имеет одинаковую монотонность. Так, при 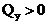эпюра 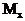возрастает слева направо; при 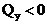- убывает.

5. Порядок линии на эпюре 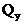всегда на единицу меньше, чем на эпюре 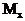. Например, если эпюра 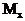- квадратная парабола, то эпюра 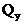на этом участке - наклонная прямая; если эпюра 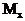- наклонная прямая, то эпюра 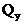на этом участке - прямая, параллельная оси; если (прямая, параллельная оси), то на этом участке .

Пример 7.

Рассмотрим жесткозащемленную плоскую раму (рис.11,а). В жесткой заделке рамы в общем случае нагружения возникают три опорные реакции: две силы ( 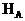и ) и 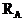опорный момент ( 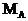). Для построения эпюр определение этих реакций не является безусловной необходимостью: расчет, как и в случае жесткозащемленной балки, можно вести от свободного конца, то есть всякий раз так выбирать отсеченную часть для рассматриваемого сечения, чтобы в нее не попадала опора с неизвестными опорными реакциями. Тем не менее, иногда целесообразно вычислить опорные реакции. Это позволяет проверить построение эпюр или облегчить их построение. Для вычисления реакций в жесткозащемленной раме используются три условия равновесия:

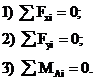
Построим эпюры 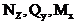для рассматриваемой рамы, не вычисляя опорные реакции.

Методика построения эпюр аналогична ранее рассмотренной для балок , т.е. сначала необходимо наметить характерные сечения. В дополнение к ранее указанным (см.1.2), в рамах характерными являются также сечения, расположенные бесконечно близко к жесткому узлу на всех элементах, сходящихся в этом узле.

Построение эпюры 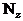. Следуя установленным правилам, в рассматриваемой раме можно выделить 8 характерных сечений. Продольная сила в любом из них численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня. При этом следует учитывать, что положение продольной оси будет изменяться в зависимости от того, чему принадлежит рассматриваемое сечение - стойкам или ригелю.

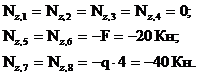
Построение эпюры 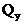. Поперечная сила в любом сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную ось рамы. Положение поперечной оси также будет изменяться в зависимости от принадлежности данного сечения стойкам или ригелю. С учетом правила знаков, двигаясь от свободного конца к жесткой заделке, получим для :

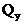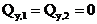(проекция пары М на любую ось равна нулю);

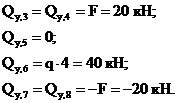
Необходимо обратить внимание на тот факт, что 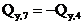, т.е. что поперечная сила в верхних сечениях противоположных стоек от действия силы, приложенной к правой стойке (при заделке, расположенной слева, и наоборот) имеет противоположные знаки. Отчасти это можно объяснить противоположными направлениями оси y для сечений 4 и 7, но более строгое обоснование указанного равенства будет дано ниже.

Построение эпюры 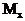. Изгибающий момент в любом сечении численно равен алгебраической сумме моментов всех нагрузок, приложенных по одну сторону от рассматриваемого сечения, относительно этого сечения (более строго: относительно оси x этого сечения). Обратим внимание на два важных замечания:

1) составляющая момента 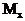от действия сосредоточенного момента М всегда одинакова и равна М;

2) под плечом силы всегда понимается длина перпендикуляра, опущенного из центра тяжести данного сечения на линию действия силы. Это означает, что, например, плечо силы F для сечений 4-7 одинаково и равно 3 м.

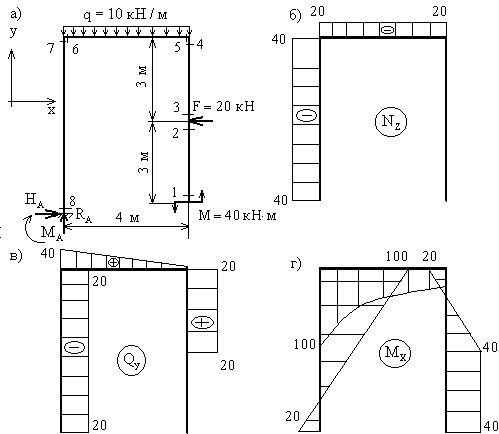
Рис. 11

Таким образом, для сечений 1-8 получим:

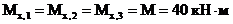(сжатым является правое волокно в сечениях 1-3, поэтому ордината отложена вправо от оси стойки);

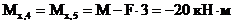(знаки "+" и "-" здесь имеют относительный характер; результирующий момент сжимает левые волокна в сечении 4 и нижние волокна в сечении 5, поэтому ордината "20" откладывается соответственно влево и вниз);

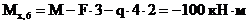(сжаты нижние волокна);

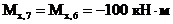(сжаты правые волокна);

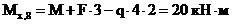(сжаты левые волокна).

Между 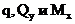в плоских рамах сохраняются те же зависимости, что и в балках, а именно:

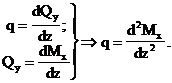
Из этого следует, что правила контроля эпюр 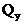и 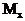остаются теми же, что и для балок ,( см. 1.11).

Эпюры 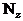в плоских рамах строятся наиболее просто и при отсутствии нагрузок, распределенных вдоль стержней, представляют собой графически отрезки прямых, параллельные осям стержней ( или совпадают с ними при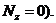

Если проанализировать процесс построения эпюр (рис.11,б-г), то очевидно, что наиболее "сложно" вычислять ординаты в сечениях стержня, примыкающего к заделке ( на рис.11,б-г это сечения 7 и 8). Как уже отмечалось, с этой целью иногда вычисляют реакции 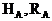и момент .

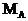При принятом для всей рамы направлении осей 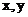(рис.11,а) уравнения равновесия имеют вид:

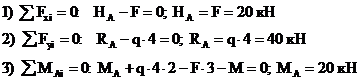
Полученный для каждой из величин 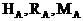знак "+" говорит, что направления их были выбраны правильно.

После вычисления опорных реакций значения величин 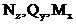в сечениях 7 и 8 (как, впрочем, и в любом другом) можно вычислять, двигаясь от жесткой заделки к свободному концу.

Например, для сечений 7 и 8:

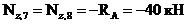(знак "-" указывает на сжатие в этих сечениях с силой );

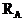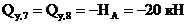(т.к. реакция 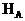стремится повернуть каждое из этих сечений против часовой стрелки.)

При сравнении величины 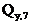с ранее полученной величиной 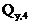видно, что

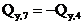, о чем уже говорилось выше.

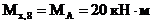(сжаты левые волокна стойки);

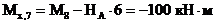(сжаты правые волокна стойки).

Разумеется, результаты получаемые для любого сечения при движении от свободного конца к жесткой заделке и при движении в обратном направлении одинаковы.

Пример 8.

Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере, но с шарнирным опиранием (рис.12,а).

Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией.

Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:

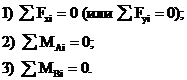
Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию.

Так, в рассматриваемом примере этим условием будет 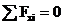, которое будет содержать неизвестную реакцию 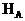(в то время как условие 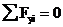содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие .

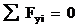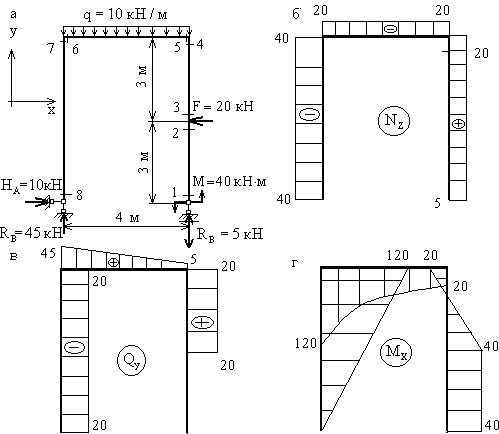
Рис. 12

Второе и третье уравнения равновесия ( 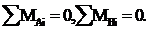) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения ( иногда - с нулевым плечом).

В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть .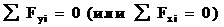

Построение эпюр 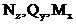в шарнирных рамах выполняется так же, как и в защемленных, но " с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.

Вычислим реакции опор рамы (рис.12,а)

Уравнения статики:

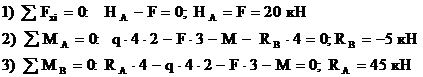
Знак "-", полученный при вычислении реакции 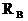, говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:

,

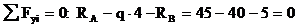то есть реакции опор вычислены правильно.

Построение эпюры .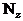

Двигаясь по оси рамы от сечения 1 к сечению 6, получим:

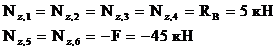
Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:

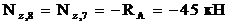
Этот же результат получим из рассмотрения отсеченной части 1-6:

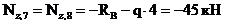
Этот же результат получим из рассмотрения отсеченной части 1-6:

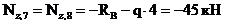
По вычисленным значениям строим эпюру ( рис.12,б)

Построение эпюры .

Из рассмотрения отсеченной части 1-5:

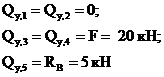
Из рассмотрения отсеченной части 8-6:

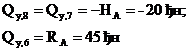
Эпюра , построенная по вычисленным значениям, показана на рис.12,в.

Построение эпюры .

Из рассмотрения отсеченной части 1-5:

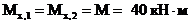(сжаты правые волокна стойки);

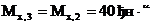(плечо силы F равно нулю);

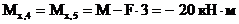(сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);

Из рассмотрения отсеченной части 8 -6:

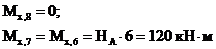
(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно).

Эпюра 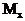показана на рис12,г.

Пример 9. Рассмотрим шарнирную раму более сложной конфигурации (рис.13,а).

Здесь необходимо рассматривать 10 характерных сечений для построения эпюр 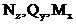. Сечения 1-6 расположены на ригеле слева направо, а сечения 7-10 - на стойке сверху вниз. Как и в предыдущем примере, указанное расположение характерных сечений является безусловно необходимым, а их нумерация - произвольной.

Уравнения статики для вычисления опорных реакций имеют вид:

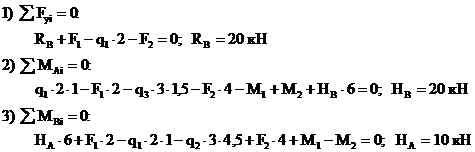
Проверка вычисления опорных реакций:

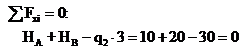
При построении эпюр 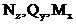целесообразно выбирать отсеченную часть, продвигаясь к центральному узлу рамы с четырех сторон, т.к. в этом случае определение внутренних силовых факторов в каждом из характерных сечений осуществляется наиболее просто.

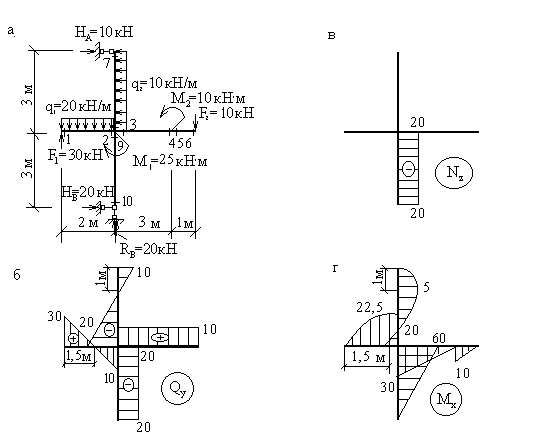
Рис. 13

Построение эпюр .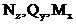

Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):

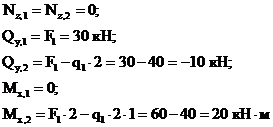(сжаты верхние волокна).

Из рассмотрения правой отсеченной части (сечения 3-6):

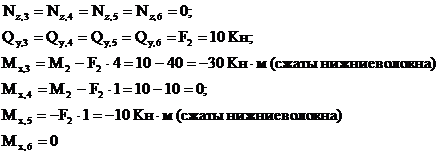
Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):

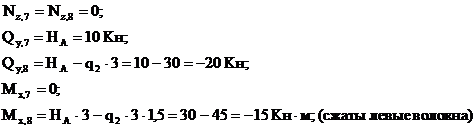
Из рассмотрения нижней отсеченной части (сечения 9-10):

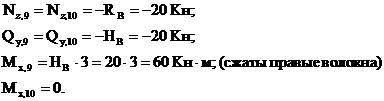
Характер эпюры 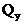на участках рамы с распределенными нагрузкам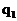и и 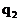, а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент 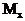принимает экстремальные значения. Определение положений точек пересечения (т.е. тех точек, где ) выполняется так же, как и в балках (см. 1.9).

Вычислим экстремальные значения момента .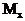

На участках под распределенной нагрузкой :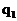

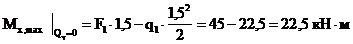(сжаты верхние волокна).

На участке с распределенной нагрузкой :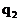

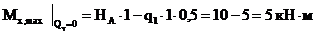(сжаты правые волокна).

Эпюры 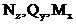показаны на рис.13,б,в,г.

Теорема о взаимности работ

Рассмотрим два состояния упругой системы, находящейся в равновесии. В каждом из этих состояний на систему действует некоторая статическая нагрузка (рис.23,а). Обозначим перемещения по направлениям сил F₁ и F₂ через , где индекс “i” показывает направление перемещения, а индекс “j” – вызвавшую его причину.

Рис. 23

Обозначим работу нагрузки первого состояния (сила F₁) на перемещениях первого состояния через А₁₁, а работу силы F₂ на вызванных ею перемещениях – А₂₂:

.

Используя (2.9), работы А₁₁ и А₂₂ можно выразить через внутренние силовые факторы:

(2.10)

Рассмотрим случай статического нагружения той же системы (рис.23,а) в такой последовательности. Сначала к системе прикладывается статически возрастающая сила F₁ (рис.23,б); когда процесс ее статического нарастания закончен, деформация системы и действующие в ней внутренние усилия становятся такими же, как и первом состоянии (рис.23,а). Работа силы F₁ составит:

Затем на систему начинает действовать статически нарастающая сила F₂ (рис.23,б). В результате этого система получает дополнительные деформации и в ней возникают дополнительные внутренние усилия, такие же, как и во втором состоянии (рис.23,а). В процессе нарастания силы F₂ от нуля до ее конечного значения сила F₁ , оставаясь неизменной, перемещается вниз на величину дополнительного прогиба и, следовательно, совершает дополнительную работу:

Сила F₂ при этом совершает работу:

Полная работа А при последовательном нагружении системы силами F₁, F₂ равна:

(2.11)

С другой стороны, в соответствии с (2.4) полную работу можно определить в виде:

(2.12)

Приравнивая друг к другу выражения (2.11) и (2.12), получим:

(2.13)

или

А₁₂=А₂₁ (2.14)

Равенство (2.14) носит название теоремы о взаимности работ, или теоремы Бетти: работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второ