Предел и непрерывность функции нескольких переменных.
Лекция 1.
Функции нескольких переменных. Геометрическое изображение функции двух переменных. Линии и поверхности уровня. Предел и непрерывность функции нескольких переменных, их свойства. Частные производные, их свойства и геометрический смысл.
Определение 1.1. Переменная z (с областью изменения Z)называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.
Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.
Обозначения: z = f(x,y), z = z(x,y).
Примеры.
- z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.
-
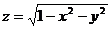 - функция, областью определения которой являются решения неравенства
- функция, областью определения которой являются решения неравенства 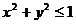 .
.
Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел 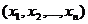 , являющихся аргументами функции нескольких переменных.
, являющихся аргументами функции нескольких переменных.
Определение 1.3. . Переменная z (с областью изменения Z)называется функцией нескольких независимых переменных 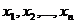 в множестве М, если каждому набору чисел
в множестве М, если каждому набору чисел 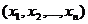 из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.
из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.
Обозначения: z = f 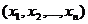 , z = z
, z = z 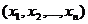 .
.
Геометрическое изображение функции двух переменных.
Рассмотрим функцию z = f(x,y), (1.1)
 определенную в некоторой области М на плоскости Оху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где
определенную в некоторой области М на плоскости Оху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где 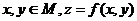 , является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.
, является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.



 z
z
z = f(x,y)
 M y
M y
Примерами могут служить изучаемые в предыдущем семестре уравнения плоскости
z = ax + by + c
и поверхностей второго порядка:
z = x² + y² (параболоид вращения),
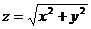 (конус) и т.д.
(конус) и т.д.

 Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n-мерном пространстве», хотя изобразить подобную поверхность невозможно.
Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n-мерном пространстве», хотя изобразить подобную поверхность невозможно.
Линии и поверхности уровня.
Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.
Пример.
Найдем линии уровня для поверхности z = 4 – x² - y². Их уравнения имеют вид x² + y² = 4 – c (c=const) – уравнения концентрических окружностей с центром в начале координат и с радиусами 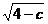 . Например, при с=0 получаем окружность x² + y² = 4 .
. Например, при с=0 получаем окружность x² + y² = 4 .
Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.
Пример.
Для функции u = 3x + 5y – 7z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y – 7z –12 + с = 0.
Частные производные.
Рассмотрим изменение функции 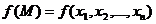 при задании приращения только одному из ее аргументов – хi , и назовем его
при задании приращения только одному из ее аргументов – хi , и назовем его 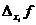 .
.
Определение 1.7. Частной производной функции 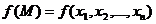 по аргументу хi называется
по аргументу хi называется 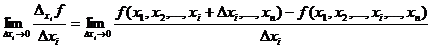 .
.
Обозначения: 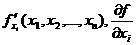 .
.
Таким образом, частная производная функции нескольких переменных определяется фактически как производная функции одной переменной – хi. Поэтому для нее справедливы все свойства производных, доказанные для функции одной переменной.
Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными.
Примеры.
1. z = 2x² + 3xy –12y² + 5x – 4y +2, 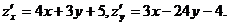
2. z = xy, 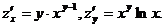
3. 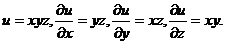
Геометрическая интерпретация частных производных функции двух переменных.
Рассмотрим уравнение поверхности z = f (x,y) и проведем плоскость х = const. Выберем на линии пересечения плоскости с поверхностью точку М (х,у). Если задать аргументу у приращение Δу и рассмотреть точку Т на кривой с координатами (х, у+Δу, z+Δyz), то тангенс угла, образованного секущей МТ с положительным направлением оси Оу, будет равен 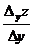 . Переходя к пределу при
. Переходя к пределу при 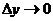 , получим, что частная производная
, получим, что частная производная 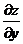 равна тангенсу угла, образованного касательной к полученной кривой в точке М с положительным направлением оси Оу. Соответственно частная производная
равна тангенсу угла, образованного касательной к полученной кривой в точке М с положительным направлением оси Оу. Соответственно частная производная 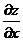 равна тангенсу угла с осью Ох касательной к кривой, полученной в результате сечения поверхности z = f (x,y) плоскостью y = const.
равна тангенсу угла с осью Ох касательной к кривой, полученной в результате сечения поверхности z = f (x,y) плоскостью y = const.
Лекция 2.
Дифференцируемость функции нескольких переменных. Дифференциал, его свойства. Применение дифференциала к приближенным вычислениям. Дифференцирование сложных функций. Инвариантность формы дифференциала.
При исследовании вопросов, связанных с дифференцируемостью, ограничимся случаем функции трех переменных, поскольку все доказательства для большего количества переменных проводятся так же.
Определение 2.1. Полным приращениемфункции u = f(x, y, z) называется
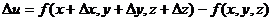 (2.1)
(2.1)
Теорема 2.1. Если частные производные 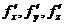 существуют в точке (х0 , у0 , z0) и в некоторой ее окрестности и непрерывны в точке (x0 , y0 , z0) , то
существуют в точке (х0 , у0 , z0) и в некоторой ее окрестности и непрерывны в точке (x0 , y0 , z0) , то
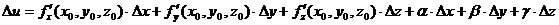 , (2.2)
, (2.2)
где α, β, γ – бесконечно малые, зависящие от Δх, Δу, Δz.
Доказательство.
Представим полное приращение Δu в виде:
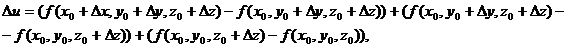 ,
,
где каждая разность представляет собой частное приращение функции только по одной из переменных. Из условия теоремы следует, что к этим разностям можно применить теорему Лагранжа. При этом получим:
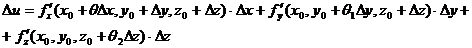 .
.
Так как по условию теоремы частные производные непрерывны в точке (х0 , у0 , z0), можно представить их в виде:
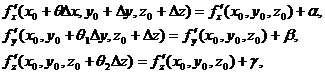
где 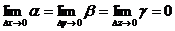 . Теорема доказана.
. Теорема доказана.
Можно показать, что 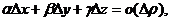 где
где 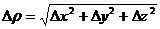 . Действительно, α, β и γ – бесконечно малые при ρ→0, а
. Действительно, α, β и γ – бесконечно малые при ρ→0, а 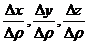 - ограниченные (т.к. их модули не превышают 1).
- ограниченные (т.к. их модули не превышают 1).
Тогда приращение функции, удовлетворяющей условиям теоремы 2.1, можно представить в виде: 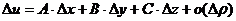 , (2.3)
, (2.3)
где 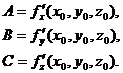 (2.4)
(2.4)
Определение 2.2. Если приращение функции u = f (x, y, z) в точке (x0 , y0 , z0) можно представить в виде (2.3), (2.4), то функция называется дифференцируемой в этой точке, а выражение 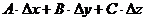 - главной линейной частью приращенияили полным дифференциалом рассматриваемой функции.
- главной линейной частью приращенияили полным дифференциалом рассматриваемой функции.
Обозначения: du, df (x0 , y0 , z0).
Так же, как в случае функции одной переменной, дифференциалами независимых переменных считаются их произвольные приращения, поэтому

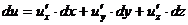 (2.5)
(2.5)
Замечание 1. Итак, утверждение «функция дифференцируема» не равнозначно утверждению «функция имеет частные производные» - для дифференцируемости требуется еще и непрерывность этих производных в рассматриваемой точке.
Замечание 2. Если в формуле (2.5) считать 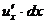 ,
, 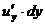 и
и 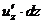 частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов.
частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов.
Применение дифференциала к приближенным вычислениям.
По аналогии с линеаризацией функции одной переменной можно при приближенном вычислении значений функции нескольких переменных, дифференцируемой в некоторой точке, заменять ее приращение дифференциалом. Таким образом, можно находить приближенное значение функции нескольких (например, двух) переменных по формуле:
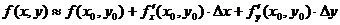 , (2.6)
, (2.6)
где 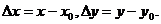
Пример.
Вычислить приближенное значение 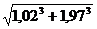 .
.
Рассмотрим функцию 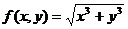 и выберем х0 =1, у0 = 2. Тогда Δх = 1,02 – 1 = 0,02; Δу = 1,97 – 2 = -0,03. Найдем
и выберем х0 =1, у0 = 2. Тогда Δх = 1,02 – 1 = 0,02; Δу = 1,97 – 2 = -0,03. Найдем 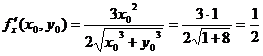 ,
,
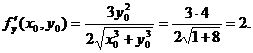 Следовательно, учитывая, что f (1, 2) = 3, получим:
Следовательно, учитывая, что f (1, 2) = 3, получим:
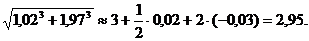
Лекция 5.
Условный экстремум.
Определение 5.4. Если аргументы функции f (x1 , x2 ,…, xn) связаны дополнительными условиями в виде m уравнений (m < n):
φ1 (х1, х2 ,…, хn) = 0, φ2 (х1, х2 ,…, хn) = 0, …, φm (х1, х2 ,…, хn) = 0, (5.2)
где функции φi имеют непрерывные частные производные, то уравнения (5.2) называются уравнениями связи.
Определение 5.5. Экстремум функции f (x1 , x2 ,…, xn) при выполнении условий (5.2) называется условным экстремумом.
Замечание. Можно предложить следующее геометрическое истолкование условного экстремума функции двух переменных: пусть аргументы функции f(x,y) связаны уравнением φ(х,у) = 0, задающим некоторую кривую в плоскости Оху. Восставив из каждой точки этой кривой перпендикуляры к плоскости Оху до пересечения с поверхностью z = f (x,y), получим пространственную кривую, лежащую на поверхности над кривой φ(х,у) = 0. Задача состоит в поиске точек экстремума полученной кривой, которые, разумеется, в общем случае не совпадают с точками безусловного экстремума функции f(x,y).
Определим необходимые условия условного экстремума для функции двух переменных, введя предварительно следующее определение:
Определение 5.6. Функция L (x1 , x2 ,…, xn) = f (x1 , x2 ,…, xn) + λ1φ1 (x1 , x2 ,…, xn) +
+ λ2φ2 (x1 , x2 ,…, xn) +…+λmφm (x1 , x2 ,…, xn), (5.3)
где λi – некоторые постоянные, называется функцией Лагранжа, а числа λi – неопределенными множителями Лагранжа.
Теорема 5.3 (необходимые условия условного экстремума). Условный экстремум функции z = f (x, y) при наличии уравнения связи φ (х, у) = 0 может достигаться только в стационарных точках функции Лагранжа L (x, y) = f (x, y) + λφ (x, y).
Доказательство. Уравнение связи задает неявную зависимость у от х, поэтому будем считать, что у есть функция от х: у = у(х). Тогда z есть сложная функция от х, и ее критические точки определяются условием: 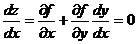 . (5.4) Из уравнения связи следует, что
. (5.4) Из уравнения связи следует, что 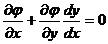 . (5.5)
. (5.5)
Умножим равенство (5.5) на некоторое число λ и сложим с (5.4). Получим:
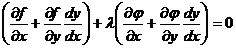 , или
, или 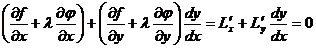 .
.
Последнее равенство должно выполняться в стационарных точках, откуда следует:
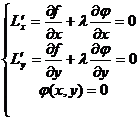 (5.6)
(5.6)
Получена система трех уравнений относительно трех неизвестных: х, у и λ, причем первые два уравнения являются условиями стационарной точки функции Лагранжа. Исключая из системы (5.6) вспомогательное неизвестное λ, находим координаты точек, в которых исходная функция может иметь условный экстремум.
Замечание 1. Проверку наличия условного экстремума в найденной точке можно провести с помощью исследования частных производных второго порядка функции Лагранжа по аналогии с теоремой 5.2.
Замечание 2. Точки, в которых может достигаться условный экстремум функции f (x1 , x2 ,…, xn) при выполнении условий (5.2), можно определить как решения системы 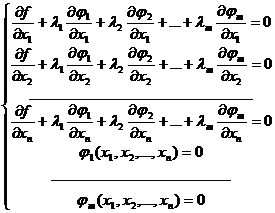 (5.7)
(5.7)
Пример. Найдем условный экстремум функции z = xy при условии х + у = 1. Составим функцию Лагранжа L(x, y) = xy + λ (x + y – 1). Система (5.6) при этом выглядит так:
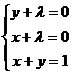 , откуда -2λ=1, λ=-0,5, х = у = -λ = 0,5. При этом L (x, y) можно представить в виде L (x, y) = -0,5 (x – y)² + 0,5 ≤ 0,5, поэтому в найденной стационарной точке L (x, y)
, откуда -2λ=1, λ=-0,5, х = у = -λ = 0,5. При этом L (x, y) можно представить в виде L (x, y) = -0,5 (x – y)² + 0,5 ≤ 0,5, поэтому в найденной стационарной точке L (x, y)  имеет максимум, а z = xy – условный максимум.
имеет максимум, а z = xy – условный максимум.
Лекция 7.
Комплексные числа, их изображение на плоскости. Алгебраические операции над комплексными числами. Комплексное сопряжение. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Корни из комплексных чисел. Показательная функция комплексного аргумента. Формула Эйлера. Показательная форма комплексного числа.
При изучении одного из основных приемов интегрирования: интегрирования рациональных дробей – требуется для проведения строгих доказательств рассматривать многочлены в комплексной области. Поэтому изучим предварительно некоторые свойства комплексных чисел и операций над ними.
Определение 7.1. Комплексным числом z называется упорядоченная пара действительных чисел (а,b) : z = (a,b) (термин «упорядоченная» означает, что в записи комплексного числа важен порядок чисел а и b: (a,b)≠(b,a) ). При этом первое число а называется действительной частью комплексного числа z и обозначается a = Re z, а второе число b называется мнимой частью z: b = Im z.
Определение 7.2. Два комплексных числа z1 = (a1 , b1) и z2 = (a2 , b2 ) равны тогда и только тогда, когда у них равны действительные и мнимые части, то есть a1 = a2, b1 = b2.
Действия над комплексными числами.
1. Суммой комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ) называется комплексное число z = (a,b) такое, что a = a1 + a2 , b = b1 + b2 . Свойства сложения: а) z1 + z2 = z2 + z1; б) z1 + (z2 + z3 ) = (z1 + z2 ) + z3; в) существует комплексное число 0 = (0,0): z + 0 = z для любого комплексного числа z.
2. Произведением комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ) называется комплексное число z = (a,b) такое, что a = a1a2 – b1b2 , b = a1b2 + a2b1 . Свойства умножения: а) z1z2 = z2z1 ; б) z1 (z2 z3) = (z1 z2) z3, в) (z1 + z2) z3 = z1 z3 + z2 z3 .
Замечание. Подмножеством множества комплексных чисел является множество действительных чисел, определяемых как комплексные числа вида (а,0). Можно убедиться, что при этом определение операций над комплексными числами сохраняет известные правила соответствующих операций над действительными числами. Кроме того, действительное число 1 = (1,0) сохраняет свое свойство при умножении на любое комплексное число: 1∙ z = z.
Определение 7.3. Комплексное число (0, b) называется чисто мнимым . В частности, число (0,1) называют мнимой единицейи обозначают символом i.
Свойства мнимой единицы:
1) i∙i=i² = -1; 2) чисто мнимое число (0,b) можно представить как произведение действительного числа (b,0) и i : (b,0) = b∙i.
Следовательно, любое комплексное число z = (a,b) можно представить в виде: (a,b) = (a,0) + (0,b) = a + ib.
Определение 7.4. Запись вида z = a + ib называют алгебраической формой записи комплексного числа.
Замечание. Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.
Определение 7.5. Комплексное число 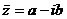 называется комплексно сопряженным числу z = a + ib.
называется комплексно сопряженным числу z = a + ib.
3. Вычитание комплексных чисел определяется как операция, обратная сложению: z =(a,b) называется разностью комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ), если a = a1 – a2 , b = b1 – b2.
4. Деление комплексных чисел определяется как операция, обратная умножению: число z = a + ib называется частным от деления z1 = a1 + ib1 и z2 = a2 + ib2 (z2 ≠ 0), если z1 = z∙z2. Следовательно, действительную и мнимую части частного можно найти из решения системы уравнений: a2 a – b2 b = a1 , b2 a + a2 b = b1.
Геометрическая интерпретация комплексных чисел.
Комплексное число z = (a,b) можно представить в виде точки на плоскости с координатами (a,b) или вектора с началом в начале координат и концом в точке (a,b).
При этом модуль полученного вектора называется модулем комплексного числа, а угол, образованный вектором с положительным направлением оси абсцисс,- аргументом числа. Учитывая, что a = ρ cos φ, b = ρ sin φ, где ρ = | z | - модуль z, а φ = arg z – его аргумент, можно получить еще одну форму записи комплексного числа:
Определение 7.6. Запись вида
z = ρ (cos φ + isin φ) (7.1)
называется тригонометрической формойзаписи комплексного числа.
В свою очередь, модуль и аргумент комплексного числа можно выразить через а и b: 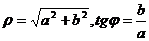 . Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.
. Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.
Легко убедиться, что операция сложения комплексных чисел соответствует операции сложения векторов. Рассмотрим геометрическую интерпретацию умножения. Пусть 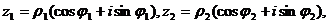 тогда
тогда 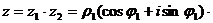
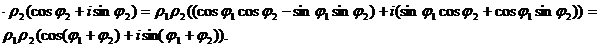
Следовательно, модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент – сумме их аргументов. Соответственно, при делении модуль частного равен отношению модулей делимого и делителя, а аргумент – разности их аргументов.
Частным случаем операции умножения является возведение в степень:
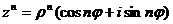 (7.2)
(7.2)
- формула Муавра.
Используя полученные соотношения, перечислим основные свойства комплексно сопряженных чисел:
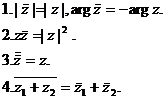
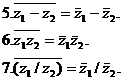
Многочлены и их корни. Теорема Безу. Основная теорема алгебры. Разложение многочлена на линейные множители в поле комплексных чисел. Простые и кратные корни многочлена. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители. Рациональные функции. Деление многочленов, выделение целой части рациональной функции. Правильные рациональные функции, их разложение на простейшие.
Рассмотрим в комплексной области многочлен, то есть функцию вида
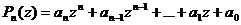 , (8.1)
, (8.1)
где 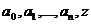 - комплексные числа. Числа
- комплексные числа. Числа 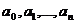 называются коэффициентами многочлена, а натуральное число n – его степенью.
называются коэффициентами многочлена, а натуральное число n – его степенью.
Определение 8.1. Два многочлена Pn (z) и 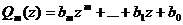 равнытогда и только тогда, когда m=n, a0 = b0 , a1 = b1 ,…, an = bn .
равнытогда и только тогда, когда m=n, a0 = b0 , a1 = b1 ,…, an = bn .
Определение 8.2. Число z0 называется корнем многочлена (8.1), если Pn (z0) = 0.
Теорема 8.1 (теорема Безу). Остаток от деления многочлена Pn(z) на z – z0 ( z0 – не обязательно корень многочлена) равен P(z0).
Доказательство. Разделив P(z) на z – z0 , получим: P(z) = Q(z)(z – z0) + r, где число r – остаток от деления, а Q(z) – многочлен степени, меньшей n. При подстановке в это равенство z = z0 найдем, что r = P(z0), что и требовалось доказать.
Теорема 8.2 (основная теорема алгебры). Всякий многочлен в комплексной области имеет корень (без доказательства).
Рациональные дроби.
Если P(z) и Q(z) – многочлены в комплексной области, то 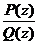 - рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q. Любую неправильную дробь можно представить в виде:
- рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q. Любую неправильную дробь можно представить в виде: 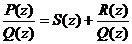 , где P(z) = Q(z) S(z) + R(z), a R(z) – многочлен, степень которого меньше степени Q(z). Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как
, где P(z) = Q(z) S(z) + R(z), a R(z) – многочлен, степень которого меньше степени Q(z). Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как 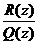 является правильной дробью.
является правильной дробью.
Лемма 1. Если 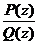 - правильная рациональная дробь и z0 – корень ее знаменателя кратности k, т.е.
- правильная рациональная дробь и z0 – корень ее знаменателя кратности k, т.е. 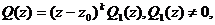 то существуют число А и многочлен P1(z) такие, что
то существуют число А и многочлен P1(z) такие, что
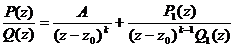 , (8.4)
, (8.4)
где последнее слагаемое является правильной дробью.
Доказательство.
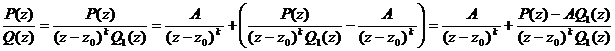 . При этом последнее слагаемое является правильной дробью. Выберем число А так, чтобы z0 было корнем многочлена P(z) – AQ1(z), то есть
. При этом последнее слагаемое является правильной дробью. Выберем число А так, чтобы z0 было корнем многочлена P(z) – AQ1(z), то есть 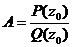 . Тогда по теореме Безу
. Тогда по теореме Безу 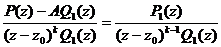 . Лемма доказана.
. Лемма доказана.
Замечание. Если коэффициенты многочленов Р и Q и выбранный корень знаменателя – действительные числа, то и коэффициенты многочленов P1 и Q1 – тоже действительные числа.
Теорема 8.3. Если 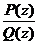 - правильная рациональная дробь и
- правильная рациональная дробь и 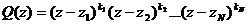 , то существуют такие комплексные числа
, то существуют такие комплексные числа 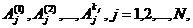 что
что
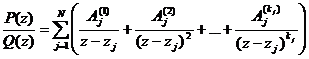 . (8.5)
. (8.5)
Доказательство.
Применив k1 раз лемму 1 к дроби 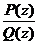 , получим:
, получим:
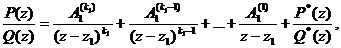 где
где 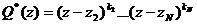 . Применяя затем ту же лемму к остальным корням знаменателя, придем к формуле (8.5).
. Применяя затем ту же лемму к остальным корням знаменателя, придем к формуле (8.5).
Лемма 2. Пусть Р(х) и Q(x) – многочлены с действительными коэффициентами, причем Q(x) = ( x² + px + q)m Q1(x), где p² - 4q < 0. Тогда существуют такие действительные числа В, С и многочлен с действительными коэффициентами Р1(х), что
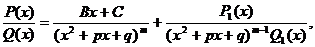 (8.6)
(8.6)
где последнее слагаемое тоже является правильной дробью.
Доказательство.
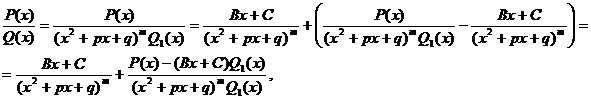 (8.7)
(8.7)
где последнее слагаемое является правильной дробью. Выберем В и С такими, чтобы число z0 =x0 +iy0 (корень многочлена z² + pz + q) было корнем многочлена P(х)-(Bх+C)Q1(х). Можно показать, что при этом 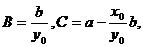 где
где 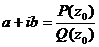 .
.
Следовательно, В и С – действительные числа, а z0 и 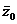 (число, комплексно сопряженное z0) – корни многочлена P(х)-(Bх+C)Q1(х). Тогда по теореме Безу он делится на
(число, комплексно сопряженное z0) – корни многочлена P(х)-(Bх+C)Q1(х). Тогда по теореме Безу он делится на
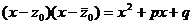 . Поэтому последнюю дробь в равенстве (8.7) можно сократить на x² + px + q и получить равенство (8.6).
. Поэтому последнюю дробь в равенстве (8.7) можно сократить на x² + px + q и получить равенство (8.6).
Используя эту лемму, можно доказать следующую теорему:
Теорема 8.4. Если 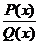 - правильная рациональная дробь, а
- правильная рациональная дробь, а
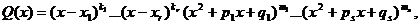 где
где 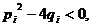 то существуют такие действительные числа
то существуют такие действительные числа 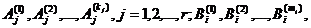
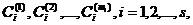 что
что
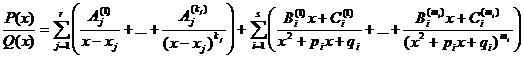 . (8.8)
. (8.8)
Примеры.
1. 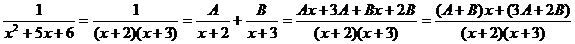 . Полученная дробь должна совпадать с исходной при любых х, следовательно, коэффициенты при одинаковых степенях х в числителях обеих дробей должны быть равными. Отсюда
. Полученная дробь должна совпадать с исходной при любых х, следовательно, коэффициенты при одинаковых степенях х в числителях обеих дробей должны быть равными. Отсюда 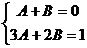 , то есть А = 1, В = -1. Следовательно, исходную дробь, знаменатель которой имеет только действительные корни (причем простые, то есть кратности 1) можно представить в виде:
, то есть А = 1, В = -1. Следовательно, исходную дробь, знаменатель которой имеет только действительные корни (причем простые, то есть кратности 1) можно представить в виде: 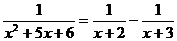 .
.
2. 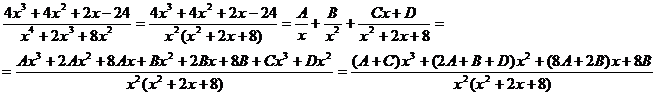
Приравнивая коэффициенты при одинаковых степенях х в числителях, получаем:
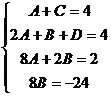 , откуда А = 1, В = -3, С = 3, D = 5. Таким образом, данную дробь, знаменатель которой имеет действительный корень х = 0 кратности 2 и комплексно сопряженные корни
, откуда А = 1, В = -3, С = 3, D = 5. Таким образом, данную дробь, знаменатель которой имеет действительный корень х = 0 кратности 2 и комплексно сопряженные корни 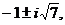 преобразуем в сумму дробей:
преобразуем в сумму дробей:
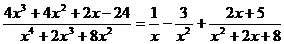 .
.
Лекция 9. Интегрирование простейших и произвольных правильных дробей. Интегрирование произвольных рациональных функций. Интегрирование дробно-линейных иррациональностей.
В пошлой лекции было показано, что любую правильную рациональную дробь можно представить в виде линейной комбинации дробей вида:
1) 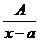 , 2)
, 2) 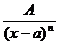 , 3)
, 3) 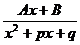 , 4)
, 4) 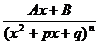
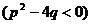 . (9.1)
. (9.1)
Эти дроби называются простейшими (или элементарными) дробями. Выясним, каким образом они интегрируются.
1) 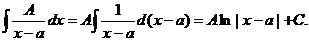
2) 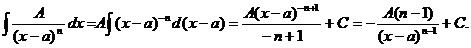 (9.2)
(9.2)
3) 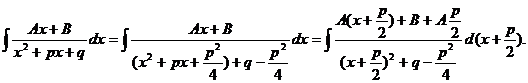 (9.3)
(9.3)
Сделаем замену 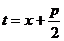 и обозначим
и обозначим 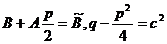 . Тогда требуется вычислить интеграл
. Тогда требуется вычислить интеграл 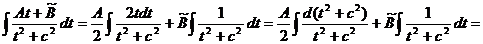
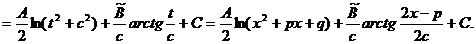 (9.4)
(9.4)
4) При интегрировании простейших дробей последнего типа воспользуемся той же заменой, что и в предыдущем случае, и представим подынтегральное выражение в виде:
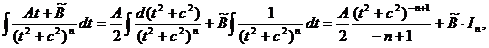 где
где 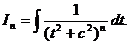 Рассмотрим отдельно способ интегрирования In .
Рассмотрим отдельно способ интегрирования In .
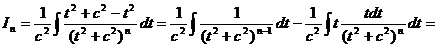
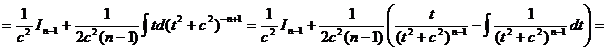
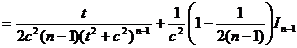 . (9.5)
. (9.5)
Таким образом, получена рекуррентная формула, позволяющая в конечном счете свести вычисление этого интеграла к 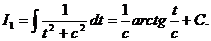
Итак, интеграл от любой простейшей дроби находится в явном виде и является элементарной функцией.
Теорема 9.1. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.
Доказательство.
Представим рациональную дробь 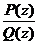 в виде:
в виде: 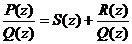 (см. лекцию 8). При этом последнее слагаемое является правильной дробью, и по теореме 8.4 ее можно представить в виде линейной комбинации простейших дробей. Таким образом, интегрирование рациональной дроби сводится к интегрированию многочлена S(x) и простейших дробей, первообразные которых, как было показано, имеют вид, указанный в теореме.
(см. лекцию 8). При этом последнее слагаемое является правильной дробью, и по теореме 8.4 ее можно представить в виде линейной комбинации простейших дробей. Таким образом, интегрирование рациональной дроби сводится к интегрированию многочлена S(x) и простейших дробей, первообразные которых, как было показано, имеют вид, указанный в теореме.
Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.
Пример.
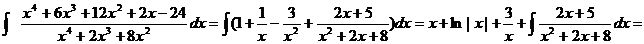
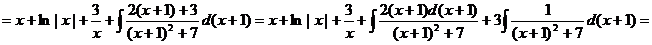
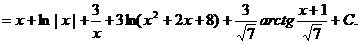
Интегрирование дробно-линейных иррациональностей.
Из ранее доказанного следует, что любую рациональную дробь можно проинтегрировать, поэтому в дальнейшем будем считать задачу интегрирования функции выполненной, если удается представить эту функцию в виде рациональной дроби. В частности, для интегралов вида 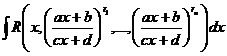 , где R – рациональная функция (многочлен или рациональная дробь), r1 ,…,rn – дроби с одним и тем же знаменателем m
, где R – рациональная функция (многочлен или рациональная дробь), r1 ,…,rn – дроби с одним и тем же знаменателем m 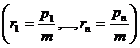 , а
, а 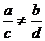 , замена
, замена 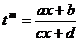 приводит к
приводит к 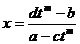 . Таким образом, х является рациональной функцией t, следовательно, его производная тоже будет рациональной функцией. Кроме того,
. Таким образом, х является рациональной функцией t, следовательно, его производная тоже будет рациональной функцией. Кроме того, 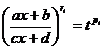 - тоже рациональные функции от t (так как pi – целое число). Поэтому после замены подынтегральное выражение примет вид R1 (t)dt , где R1 – рациональная функция, интегрируемая описанными выше способами.
- тоже рациональные функции от t (так как pi – целое число). Поэтому после замены подынтегральное выражение примет вид R1 (t)dt , где R1 – рациональная функция, интегрируемая описанными выше способами.
Замечание. С помощью подобных замен можно интегрировать функции вида 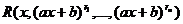 , и, в частности,
, и, в частности, 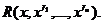
Примеры.
1. 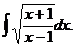 Сделаем замену
Сделаем замену 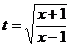 , тогда
, тогда 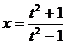 , а
, а 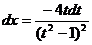 . Следовательно,
. Следовательно,
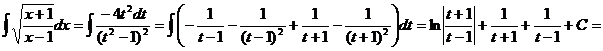
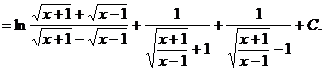
2. 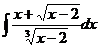 . Так как
. Так как 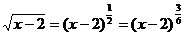 , а
, а 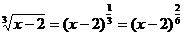 , выберем в качестве новой переменной
, выберем в качестве новой переменной 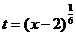 . Тогда
. Тогда 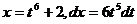 . Поэтому
. Поэтому
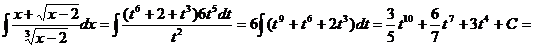
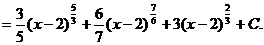
Лекция 10. Интегрирование рациональных тригонометрических выражений. Интегрирование квадратичных иррациональностей. Интегрируемость в элементарных функциях.
Рассмотрим интегрирование некоторых тригонометрических выражений.
1. Интегралы вида 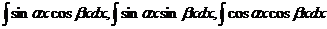 вычисляются с применением формул
вычисляются с применением формул 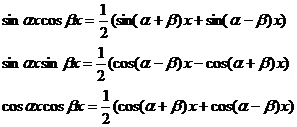 (10.1) Пример.
(10.1) Пример. 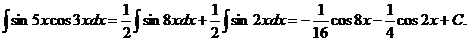
2. Интегралы вида 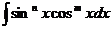 , где т и п – целые числа, интегрируются с помощью замен: а) если хотя бы одно из чисел т,п – нечетное (например, т), можно сделать замену t = sin x (или t = cos x при нечетном п). Пример 1.
, где т и п – целые числа, интегрируются с помощью замен: а) если хотя бы одно из чисел т,п – нечетное (например, т), можно сделать замену t = sin x (или t = cos x при нечетном п). Пример 1. 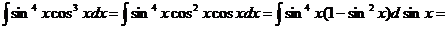
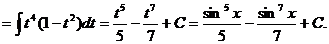 Пример 2.
Пример 2. 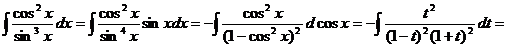
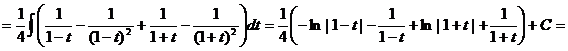
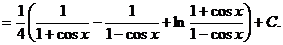 б) если т и п – четные положительные числа, можно понизить степени тригонометрических функций с помощью формул
б) если т и п – четные положительные числа, можно понизить степени тригонометрических функций с помощью формул 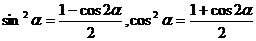 . Пример.
. Пример. 
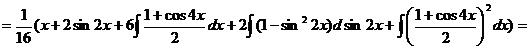
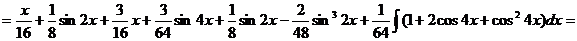
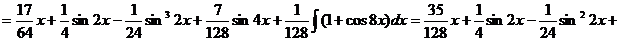
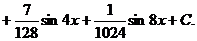 в) если т и п – четные и хотя бы одно из них отрицательно, можно применить замену t = tg x или t = ctg x. Пример.
в) если т и п – четные и хотя бы одно из них отрицательно, можно применить замену t = tg x или t = ctg x. Пример. 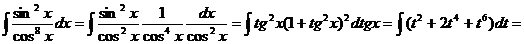

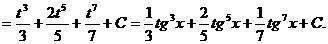
3. Интегралы вида 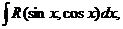 где R – рациональная функция, сводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки:
где R – рациональная функция, сводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: 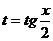 , тогда
, тогда 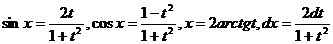 , (10.2) то есть все составляющие подынтегрального выражения представляют собой рациональные функции от t. Пример.
, (10.2) то есть все составляющие подынтегрального выражения представляют собой рациональные функции от t. Пример. 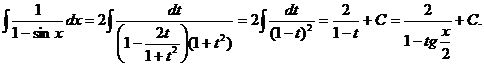 Если подынтегральная функция имеет вид R (sin²x, cos²x), можно выбрать замену t = tg x. При этом
Если подынтегральная функция имеет вид R (sin²x, cos²x), можно выбрать замену t = tg x. При этом 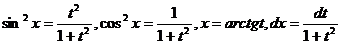 , (10.3) и степень полученной рациональной функции будет ниже, чем при универсальной тригонометрической подстановке, что облегчает дальнейшее интегрирование. Пример.
, (10.3) и степень полученной рациональной функции будет ниже, чем при универсальной тригонометрической подстановке, что облегчает дальнейшее интегрирование. Пример. 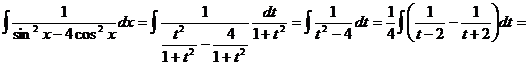
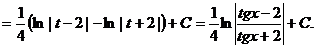
Интегрирование квадратичных иррациональностей.
При вычислении интегралов 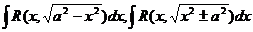 свести подынтегральную функцию к рациональной помогают замены:
свести подынтегральную функцию к рациональной помогают замены:
а) 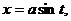 при этом
при этом 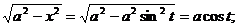 dx = acos t dt,
dx = acos t dt,  .
.
б)
