Динамическая модель межотраслевого баланса.

При рассмотрении многоотраслевой экономики приходится отказаться от нелинейности из-за возникающих при этом сложностей. Вместе с тем исследование даже линейных динамических многоотраслевых моделей также достаточно сложно, но приводит к содержательным экономическим выводам.

Здесь рассмотрим динамическое обобщение модели Леонтьева – модель динамического межотраслевого баланса.

Рассмотрим экономику, имеющую в своем составе n отраслей и производящую и потребляющую n типов товаров (продуктов).

Каждая отрасль производит один продукт, разные отрасли производят разные продукты.

Пусть 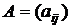– матрица прямых затрат, 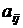не зависят от времени и масштаба.

Время в модели дискретно и изменяется через промежутки, равные году: t = 1,2,3,…,T. Так как модель будет представлена в матричной форме, то нижний индекс будем использовать как номер года.

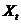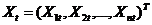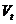В модели применяются 3n+1 переменные, характеризующие состояние экономики в динамике: – вектор–столбец валового выпуска отраслей размера n+1, , – вектор–столбец отраслевых мощностей размера n×1 (максимально возможных выпусков продукции), – вектор–столбец ввода мощностей размера n×1, 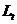– трудовые ресурсы (числовая величина 1×1).

Введем обозначения:

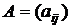– матрица прямых затрат размера n×n,

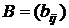– матрица фондоемкости размера n×n,

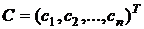– вектор–столбец потребления в расчете на одного занятого размера n×1,

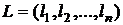– вектор–строка трудоемкости размера 1×n.

В указанных обозначениях модель выглядит следующим образом:

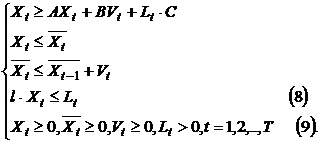(5)

(6)

(7)

Неравенства (5) показывают, что общий валовой выпуск продукции 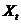должен покрывать производственные затраты 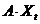, затраты продукции на расширение производственных мощностей 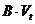и на непроизводственное потребление .

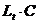Неравенства (6) ограничивают валовые выпуски отраслей наличными мощностями.

Неравенства (7) ограничивают отраслевые балансы мощностей с учетом их выбытия и ввода.

Неравенства (8) ограничивают выпуски отраслей имеющимися трудовыми ресурсами.

Лаг капиталовложений равен одному году: инвестиции, сделанные в год t, начинают работать в год t+1.

Унифицированный вектор переменных 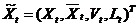, t = 1,2,3,..,T назовем допустимой траекторией, если в каждый год t выполняются все условия (5) – (9) модели.

Введем обозначения (наверху и справа блочных матриц 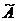и 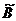порядка (3n+1) указаны размеры входящих в них матриц):

, ,

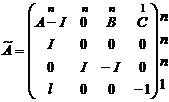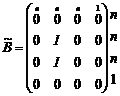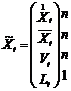
Где I – единичная матрица размера n×n.

Модель динамического межотраслевого баланса (5) – (9) приобретает унифицированную форму модели Неймана: 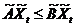, , 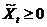t = 1,2,…,T (10)

В базовом году мощности заданы и равны 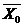и .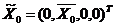

Изучение поведения траектории модели межотраслевого динамического баланса сводится к изучению траектории соответствующей модели Неймана.

Обратим внимание на экономический смысл перехода от формы (5) – (9) к форме (10).

Первую форму (5) – (9) можно рассматривать как разомкнутую форму модели в этом смысле, что часть произведенной продукции экономика затрачивает на внутренние нужды (на производственное потребление 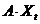и на расширение мощностей 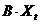), в то время как другая часть выдается в виде непроизводственного потребления .

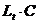Если теперь замкнуть экономику, т.е. включить потребителя в состав экономической системы, то придем к форме (10) модели динамического межотраслевого баланса. При этом домашние хозяйства рассматриваются как (n+1) –я отрасль экономики, которая потребляет продукцию других отраслей с коэффициентами прямых затрат 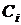, 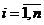и производит единственный вид продукции – труд с интенсивностью 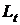. В свою очередь другие отрасли потребляют продукцию (n+1)–й отрасли (труд) с коэффициентами прямых затрат , .

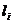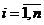Линейная модель торговли.

Одним из примеров экономического процесса приводящего к понятию собственного числа и собственного вектора матрицы, является процесс взаимных закупок товаров. Будем полагать, что бюджеты n стран, которые мы обозначим соответственно x₁, x₂,…,x_n, расходуются на покупку товаров. Будем рассматривать линейную модель обмена или модель международной торговли.

Пусть 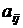– доля бюджета x_j, которую j-я страна тратит на закупку товаров у i-й страны. Если весь бюджет расходуется только на закупки внутри страны и

вне её (можно это трактовать как торговый бюджет), то , .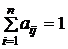

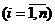Введем структурную матрицу торговли 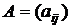, сумма элементов её любого столбца равна единице.

Для i–й страны общая выручка от внутренней и внешней торговли составит .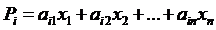

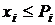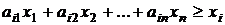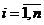При условии сбалансированной (бездефицитной) торговли для каждой страны её бюджет должен быть не больше выручки от торговли, т.е. или , (11).

Докажем, что в условиях (11) не может быть знака неравенства. Сложим все неравенства при 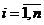. Группируя слагаемые с величинами бюджетов x_j, получим:

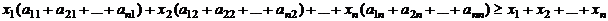
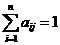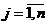Поскольку для , то 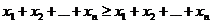, откуда возможен только знак равенства: 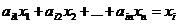, 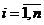(12)

Для вектора бюджетов 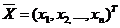систему уравнений (12) можно записать в матричной форме .

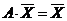Это уравнение означает, что собственный вектор структурной матрицы A, отвечающий её собственному значению 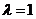, состоит из бюджетов стран бездефицитной международной торговли.

Пример. Структурная матрица торговли трех стран имеет вид 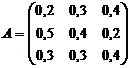. Найти бюджеты первой и второй стран, удовлетворяющие сбалансированной бездефицитной торговли, бюджет третьей страны равен 1100 усл. ед..

Решение. Необходимо найти собственный вектор 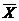, отвечающий собственному значению 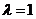заданной структурной матрицы A, то есть решить уравнение 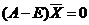, которое равносильно однородной системе:

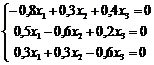
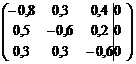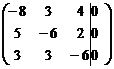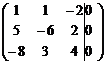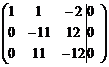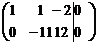~ ~ ~ ~ . Получили 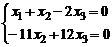, откуда , .

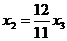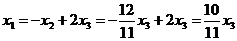По условию 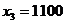усл. ед., 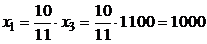усл. ед., 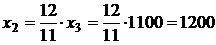усл.ед. Ответ: бюджет первой страны x₁=1000 усл. ед., второй страны x₂=1200усл. ед.