Лекция 1. Дифференциальное исчисление функции одной переменной.
Содержание
От авторов 8
Лекция 1. Дифференциальное исчисление функции одной переменной. 9
1.1.Определение производной. Механический, геометрический, экономический смысл производной. 9
1.2. Касательная и нормаль к графику функции. 10
1.3. Дифференцируемость и непрерывность. 11
Лекция 2. Правила дифференцирования. 11
2.1. Правила дифференцирования суммы, произведения и частного двух функций. 12
2.2. Производные обратной и сложной функций. 12
2.3. Производные элементарных функций. 13
Лекция 3. Дифференциал функции. 14
3.1. Условие дифференцируемости функции в точке. 14
3.2. Определение дифференциала, геометрический смысл и правила вычисления дифференциала. Использование дифференциала в приближенных вычислениях. 15
3.3. Производные и дифференциалы высших порядков. 16
Лекция 4. Основные теоремы дифференциального исчисления. 17
4.1. Теорема Ферма. 17
4.2. Теорема Ролля. 18
4.3. Теорема Лагранжа. 19
4.4. Теорема Коши. 20
4.5. Правило Лопиталя. 21
4.6. Формула Тейлора. 22
Лекция 5. Применение производных к исследованию функций. 22
5.1. Условие монотонности функции. Определение максимума и минимума функции в точке. 23
5.2. Необходимое условие существования экстремума функции одной переменной. 24
5.3. Достаточное условие существования экстремума функции одной переменной. 25
5.4. Наибольшее и наименьшее значения функции на отрезке. 25
5.5. Определение выпуклости и вогнутости графика функции. Достаточное условие выпуклости и вогнутости графика. Необходимое и достаточное условие существования точки перегиба. 26
5.6. Асимптоты графика функции. 27
Лекция 6. Функции многих переменных. 28
6.1. Определение функции двух переменных, область определения функции, график функции. 28
6.2. Определения предела и непрерывности функции двух переменных. Свойства непрерывных функций. 29
6.3. Частные производные. 31
Лекция 7. Дифференцируемость функции двух переменных. 31
7.1. Определение дифференцируемости функции двух переменных. Определение полного дифференциала. Приближенные вычисления с помощью полного дифференциала. 32
7.2. Частные производные и дифференциалы высших порядков. Теорема о равенстве смешанных частных производных. 33
7.3. Производная функции по направлению. 34
7.4. Градиент функции. 35
7.5. Экстремумы функции двух переменных. Необходимое и достаточное условия существования экстремумов. 36
Лекция 8. Метод наименьших квадратов. 37
8.1. Метод наименьших квадратов. 37
8.2. Применение метода наименьших квадратов (случай линейной зависимости). 38
8.3. Использование метода наименьших квадратов на фондовой бирже. 40
Лекция 9. Интегральное исчисление функции одной переменной. 41
9.1. Определение первообразной функции. Теорема о разности первообразных. 41
9.2. Определение неопределенного интеграла и его основные свойства. 42
9.3. Основные методы интегрирования функций. 43
Лекция 10. Интегрирование некоторых классов функций. 45
10.1. Интегрирование простейших рациональных дробей. 46
10.2. Интегрирование рациональных дробей методом разложения на простейшие дроби. 47
10.3. Интегрирование некоторых тригонометрических функций. 49
10.4. Интегрирование некоторых иррациональных выражений. Некоторые тригонометрические подстановки. 50
Лекция 11. Определенный интеграл. 52
11.1. Определение определенного интеграла. Геометрический смысл определенного интеграла. Интегрируемость функций. 52
11.2. Свойства определенного интеграла. 53
11.3. Теорема о среднем значении определенного интеграла. 54
Лекция 12. Основная формула интегрального исчисления. 55
12.1. Определенный интеграл с переменным верхним пределом интегрирования и его свойства. 55
12.2. Формула Ньютона-Лейбница - основная формула интегрального исчисления. 56
12.3. Методы интегрирования определенного интеграла. 57
12.4. Геометрические приложения определенного интеграла. 58
12.5. Несобственные интегралы. 59
Лекция 13. Дифференциальные уравнения первого порядка. 61
13.1. Определение дифференциального уравнения. Основные понятия. 61
13.2. Дифференциальные уравнения первого порядка. Основные понятия. Теорема существования и единственности решения. 62
13.3. Дифференциальные уравнения первого порядка с разделяющимися переменными. 63
13.4. Линейные дифференциальные уравнения первого порядка. 64
13.5. Однородные дифференциальные уравнения первого порядка. 66
Лекция 14. Дифференциальные уравнения второго порядка. 68
14.1. Определение дифференциальных уравнений второго порядка. Основные понятия. 68
14.2. Линейные дифференциальные уравнения второго порядка. Фундаментальная система решений. Теоремы об общем решении. 69
14.3. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. 70
14.4. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами их частные решения в зависимости от вида правой части. Метод вариации произвольных постоянных. 72
Лекция 15. Числовые ряды. 74
15.1. Определение числового ряда. Сходимость рядов, свойства сходящихся рядов. Необходимый признак сходимости числового ряда. 75
15.2. Ряды с положительными членами. Достаточные признаки сходимости положительных рядов (принцип сравнения, радикальный признак Коши, признак Даламбера). Интегральный признак Коши-Маклорена. 77
15.3. Определение знакопеременного ряда. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов. 80
Лекция 16. Степенные ряды. Функциональные ряды 81
16.1. Определение степенного ряда. 82
16.2. Теорема Абеля. Радиус сходимости степенного ряда. Дифференцирование и интегрирование степенных рядов. 82
16.3. Определение ряда Тейлора. Ряд Маклорена. 83
16.4. Разложение функции в степенной ряд. Необходимое и достаточное
условие разложения функции в степенной ряд. Достаточное условие разложения функции в степенной ряд. 84
16.5. Разложение элементарных функций в степенные ряды. 85
Лекция 17. Модели межотраслевого баланса. 86
17.1. Статическая модель межотраслевого баланса – модель Леонтьева. 86
17.2. Динамическая модель межотраслевого баланса. 90
17.3. Линейная модель торговли. 92
Лекция 18. Модели общего экономического равновесия. 94
18.1. Простейшая модель экономического равновесия. 94
18.2. Паутинообразная модель 95
18.3. Модель Эванса. 96
18.4. Модель Эрроу – Гурвица. 97
18.5. Модель рынка с прогнозируемыми ценами. 99
Лекция 19. Производственные функции и их характеристики. 101
19.1. Производственные функции и их основные характеристики. 101
19.2. Оптимальное распределение ресурсов. 104
19.3. Максимизация прибыли производства продукции. 105
19.4. Модели поведения фирмы в условиях совершенной и несовершенной конкуренции. 107
Рекомендуемая литература. 113
Посвящается Авджяну Аршавиру Семёновичу.
Уважаемый читатель! Книгой, которую ты держишь в руках, авторы попытались выразить глубокую признательность и любовь к человеку, являющемуся создателем курса лекций, который с некоторыми изменениями и дополнениями, читается до сегодняшнего дня студентам нашего университета. В книгу вошла базовая часть материала, читаемого во втором семестре. Авторы, продолжая традиции, заложенные Авджяном Аршавиром Семёновичем, надеются на то, что книга поможет вам в изучении математики.
Желаем успеха!
Теорема Ферма.
Теорема Ролля.
Теорема Лагранжа.
Теорема Коши.
Правило Лопиталя.
Формула Тейлора.
Теорема Ферма.
Теорема. Пусть функция  определена на
определена на 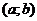 и в некоторой точке
и в некоторой точке 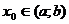 принимает наибольшее или наименьшее значение и
принимает наибольшее или наименьшее значение и  дифференцируема в точке
дифференцируема в точке 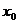 , тогда
, тогда 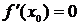
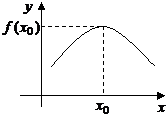 Доказательство.
Доказательство.
Для определенности положим, что в точке 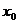
 достигает наибольшего значения, то есть
достигает наибольшего значения, то есть 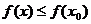 и
и 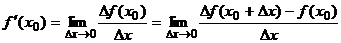 . Тогда:
. Тогда:
1) при 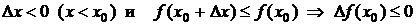 и
и 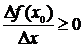
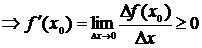 ;
;
2) при 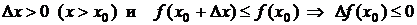 и
и 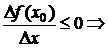
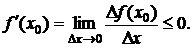 Из первого и второго следует, что
Из первого и второго следует, что 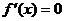 .
.
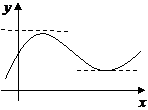 Геометрический смысл теоремы Ферма.
Геометрический смысл теоремы Ферма.
Касательная к графику функции в точках наибольшего и наименьшего значений параллельна оси абсцисс, если  дифференцируема в этих точках.
дифференцируема в этих точках.
Теорема Ролля.
Теорема.
Пусть функция 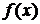 непрерывна на
непрерывна на 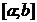 , дифференцируема на
, дифференцируема на 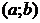 и на концах отрезка в точках a и b принимает одинаковые значения
и на концах отрезка в точках a и b принимает одинаковые значения 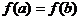 , тогда
, тогда 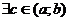 , в которой
, в которой 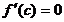 .
.
Доказательство. Если 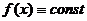 , то
, то 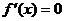 , то есть в качестве точки c можно взять любую точку, принадлежащую
, то есть в качестве точки c можно взять любую точку, принадлежащую 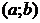 .
.
Если 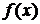 не тождественна константе, то с учетом условия о непрерывности
не тождественна константе, то с учетом условия о непрерывности 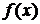 на
на 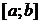 по теореме Вейерштрасса можно утверждать, что
по теореме Вейерштрасса можно утверждать, что 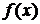 принимает на этом отрезке наибольшее и наименьшее значения в точках
принимает на этом отрезке наибольшее и наименьшее значения в точках 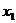 и
и 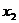 , у которых хотя бы одна попадёт внутрь
, у которых хотя бы одна попадёт внутрь 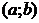 . Пусть
. Пусть  ,
, 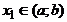 . Так как функция дифференцируема на
. Так как функция дифференцируема на 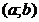 , то она дифференцируема в точке
, то она дифференцируема в точке 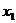 и по теореме Ферма
и по теореме Ферма 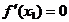 , то есть в качестве точки c можно взять точку
, то есть в качестве точки c можно взять точку 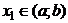 .
.
Геометрический смысл теоремы Ролля.
На 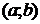 найдется хотя бы одна точка, в которой касательная параллельна оси 0X.
найдется хотя бы одна точка, в которой касательная параллельна оси 0X.
Алгебраический смысл теоремы Ролля.
Между двумя последовательными корнями дифференцируемой функции
лежит хотя бы один корень её производной.
Замечание.
Все три требования теоремы Ролля существенны. При нарушении
 хотя бы одного из них заключение теоремы может оказаться неверным.
хотя бы одного из них заключение теоремы может оказаться неверным.


Теорема Лагранжа.
Теорема.
Пусть функция  непрерывна на
непрерывна на 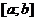 и дифференцируема на
и дифференцируема на 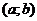 , тогда существует точка
, тогда существует точка 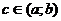 такая, что
такая, что 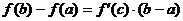 .
.
Доказательство.
Введем вспомогательную функцию 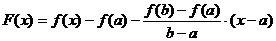 .
.
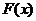 удовлетворяет всем условиям теоремы Ролля:
удовлетворяет всем условиям теоремы Ролля: 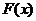 непрерывна на
непрерывна на 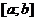 , так как на
, так как на 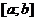 непрерывны
непрерывны  ,
, 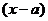 и const;
и const;
 дифференцируема на
дифференцируема на 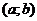 , так как на
, так как на 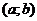 дифференцируемы
дифференцируемы  ,
, 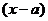 и const и существует
и const и существует 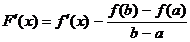 ;
;
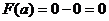 и
и 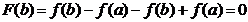 .
.
Тогда по теореме Ролля на 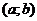 найдется точка c, в которой
найдется точка c, в которой 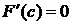 , то есть
, то есть
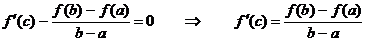 .
.
Геометрический смысл.
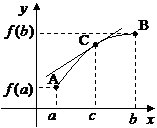 На интервале
На интервале 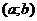 найдется хотя бы одна точка c, касательная в которой параллельна хорде, соединяющей точки
найдется хотя бы одна точка c, касательная в которой параллельна хорде, соединяющей точки 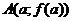 и
и 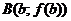 . Действительно.
. Действительно. 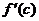 - угловой коэффициент касательной и
- угловой коэффициент касательной и 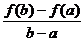 - угловой коэффициент секущей. По теореме Лагранжа они равны, следовательно касательная параллельна секущей.
- угловой коэффициент секущей. По теореме Лагранжа они равны, следовательно касательная параллельна секущей.
Теорема Коши.
Теорема.
Пусть функции  и
и 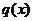 непрерывны на
непрерывны на 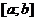 и дифференцируемы на
и дифференцируемы на 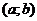 и пусть
и пусть 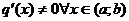 . Тогда существует точка
. Тогда существует точка 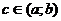 такая, что
такая, что 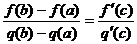 .
.
Доказательство.
Введем вспомогательную функцию 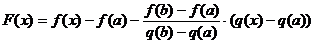 , которая удовлетворяет условиям теоремы Ролля:
, которая удовлетворяет условиям теоремы Ролля: 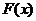 непрерывна на
непрерывна на 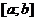 ; дифференцируема на
; дифференцируема на 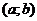 , причем
, причем 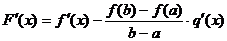 ;
; 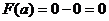 и
и 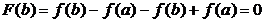 . Тогда по теореме роля найдется точка
. Тогда по теореме роля найдется точка 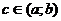 , в которой
, в которой 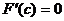 , то есть
, то есть 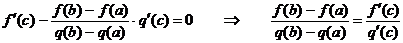 .
.
Замечание. Теорема Лагранжа является частным случаем теоремы Коши, так как в теореме Лагранжа в качестве 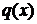 берется функция х.
берется функция х.
Правило Лопиталя.
Теорема. Пусть функции  и
и 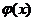 определены и дифференцируемы в некоторой окрестности точки
определены и дифференцируемы в некоторой окрестности точки 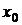 и
и 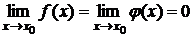 ,
, 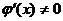 . Тогда, если существует
. Тогда, если существует 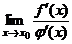 , то существует
, то существует 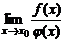 , причем
, причем 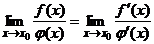 .
.
Доказательство. На отрезке 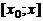 для
для  и
и 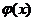 выполняются условия
выполняются условия
теоремы Коши, тогда 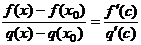 , где
, где 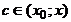 . Это равенство при учете условия
. Это равенство при учете условия 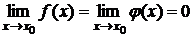 принимает вид
принимает вид 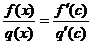 .
.
При 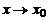 также
также 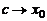 , поэтому
, поэтому 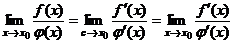 .
.
Замечание.
Правило Лопиталя можно применять неоднократно.
Теорема остается в силе, если 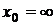 .
.
Правило Лопиталя можно применять, если 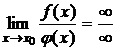 , то есть оно позволяет раскрыть неопределенности
, то есть оно позволяет раскрыть неопределенности 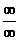 ,
, 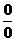 .
.
Если встречаются неопределенности 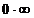 ,
, 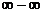 , то их надо свести к неопределенностям вида
, то их надо свести к неопределенностям вида 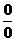 ,
, 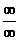 путем тождественных преобразований. Например:
путем тождественных преобразований. Например: 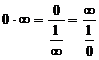 .
.
Если отыскиваются пределы показательно-степенных выражений, имеющие неопределенности вида 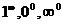 , то поступают следующим образом
, то поступают следующим образом 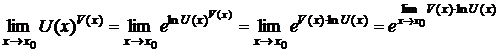 .
.
В показателе новой функции произведение 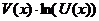 даст неопределенность вида
даст неопределенность вида 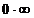 .
.
Формула Тейлора.
Теорема.
Пусть функция  имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 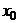 непрерывную производную до
непрерывную производную до 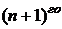 порядка включительно, тогда функцию можно представить в виде:
порядка включительно, тогда функцию можно представить в виде: 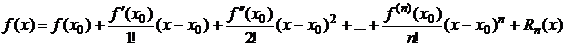 , где
, где 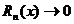 при
при 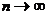 ,
, 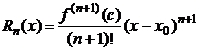 - остаточный член в форме Лагранжа,
- остаточный член в форме Лагранжа, 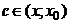 .
.
Если в формуле Тейлора считать 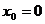 , то получим формулу Маклорена
, то получим формулу Маклорена 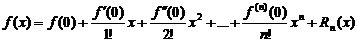 , где
, где 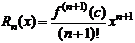 ,
, 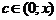 .
.
Формула Тейлора позволяет представить в окрестности точки 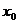 функцию
функцию 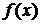 в виде суммы многочлена n-й степени
в виде суммы многочлена n-й степени 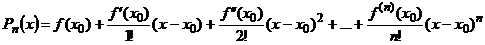 и остаточного члена
и остаточного члена 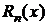 . Она позволяет оценить ошибки в приближенных равенствах, получить приближенные равенства нового типа, вычислить приближённое значение функции с помощью арифметических операций.
. Она позволяет оценить ошибки в приближенных равенствах, получить приближенные равенства нового типа, вычислить приближённое значение функции с помощью арифметических операций.
Асимптоты графика функции.
Асимптоты графика функции.
Определение. Прямая линия l называется асимптотой графика функции 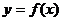 , если расстояние от текущей точки кривой до этой прямой стремится к нулю при неограниченном удалении текущей точки кривой от начала координат.
, если расстояние от текущей точки кривой до этой прямой стремится к нулю при неограниченном удалении текущей точки кривой от начала координат.
Асимптоты бывают двух видов: вертикальные и наклонные.
Вертикальные асимптоты имеют уравнение 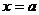 , при этом хотя бы один из пределов функции при
, при этом хотя бы один из пределов функции при 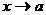 должен быть равен
должен быть равен 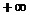 или
или 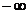 . Вертикальные асимптоты ищут на границах области определения функции и в точках бесконечного разрыва функции.
. Вертикальные асимптоты ищут на границах области определения функции и в точках бесконечного разрыва функции.
Наклонные асимптоты имеют уравнение 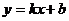 . Их ищут по двум направлениям при
. Их ищут по двум направлениям при 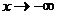 ,
, 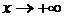 по формулам
по формулам
 ,
, 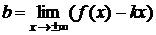 .
.
Частным видом наклонных асимптот являются горизонтальные асимптоты, которые имеют место при 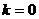 .
.
Уравнение горизонтальных асимптот 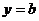 . Если хотя бы один из пределов для нахождения k или b не существует, или бесконечен, то наклонных асимптот в данном направлении нет.
. Если хотя бы один из пределов для нахождения k или b не существует, или бесконечен, то наклонных асимптот в данном направлении нет.
Схема нахождения асимптот:
1) найти область определения функции;
2) найти вертикальные асимптоты на основе области определения;
3) найти наклонные асимптоты по формулам для вычисления k и b при 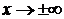 .
.
Определения предела и непрерывности функции двух переменных. Свойства непрерывных функций.
Частные производные.
6.1. Определение функции двух переменных, область определения функции, график функции.
Для упрощения ограничимся рассмотрением функции двух переменных. Все дальнейшее справедливо и для функции многих переменных.
Определение. Если по какому-либо закону или правилу каждой паре 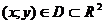 независимых переменных ставится в соответствие вполне определенное значение z, то говорят, что на множестве D определена функция двух переменных
независимых переменных ставится в соответствие вполне определенное значение z, то говорят, что на множестве D определена функция двух переменных  .
.
Область определения D функции двух переменных является некоторым подмножеством точек плоскости 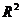 .
.
Определение. Графиком функции двух переменных  является множество точек пространства
является множество точек пространства 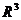 вида
вида 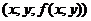 , где
, где 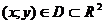 и D - область определения функции двух переменных.
и D - область определения функции двух переменных.
Определения предела и непрерывности функции двух переменных. Свойства непрерывных функций.
Пусть  определена на множестве
определена на множестве 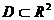 и точка
и точка  - предельная точка множества D (т.е. любая окрестность точки
- предельная точка множества D (т.е. любая окрестность точки  содержит точки множества D, отличные от точки
содержит точки множества D, отличные от точки  ). Расстояние между точками
). Расстояние между точками 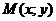 и
и  определяется по формуле
определяется по формуле 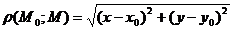 .
.
Определение. Число A называется пределом функции 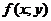 при
при
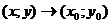 , если для любого положительного числа
, если для любого положительного числа 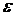 найдется число
найдется число 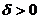 , зависящее от
, зависящее от 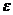 такое, что
такое, что 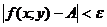 как только
как только 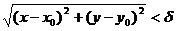 при
при 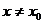 и
и 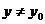 .
.
Замечание.
Неравенство 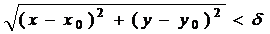 определяет
определяет 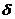 окрестность точки
окрестность точки 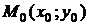 или множество точек
или множество точек 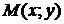 , расстояние которых до точки
, расстояние которых до точки 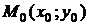 меньше
меньше 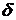 :
: 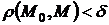 .
.
Все правила вычисления и свойства пределов для функции одной переменной справедливы для и функции двух переменных.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если
предел этой функции в точке  совпадает со значением функции в точке
совпадает со значением функции в точке  , то есть
, то есть 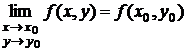 .
.
Придадим аргументам 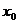 и
и 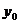 приращения
приращения 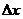 и
и 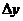 так, чтобы точки
так, чтобы точки 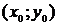 ,
, 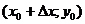 ,
, 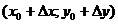 и
и 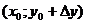 принадлежали области определения функции. Тогда:
принадлежали области определения функции. Тогда:
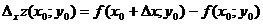 - частное приращение функции z по переменной x в точке
- частное приращение функции z по переменной x в точке  ;
;
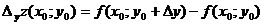 - частное приращение функции z по переменной y в точке
- частное приращение функции z по переменной y в точке  ;
;
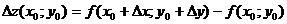 - полное приращение функции в точке
- полное приращение функции в точке  .
.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции, то есть
, если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции, то есть 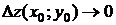 при
при 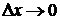 и
и 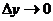 .
.
Данные определения непрерывности функции эквивалентны.
Свойства функций, непрерывных на ограниченном замкнутом множестве.
Теорема 1. Если функция  непрерывна на ограниченном замкнутом множестве, то она ограничена на этом множестве.
непрерывна на ограниченном замкнутом множестве, то она ограничена на этом множестве.
Теорема 2. Если функция  непрерывна на ограниченном замкнутом множестве, то на этом множестве она достигает своего наименьшего и наибольшего значений.
непрерывна на ограниченном замкнутом множестве, то на этом множестве она достигает своего наименьшего и наибольшего значений.
Теорема 3. Если функция  непрерывна на ограниченном замкнутом множестве и в двух точках этого множества принимают значения разных знаков, то на этом множестве найдется точка
непрерывна на ограниченном замкнутом множестве и в двух точках этого множества принимают значения разных знаков, то на этом множестве найдется точка 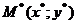 , в которой функция обращается в ноль, то есть
, в которой функция обращается в ноль, то есть 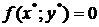 .
.
Частные производные.
Пусть функция  определена на множестве
определена на множестве  , точки
, точки  ,
, 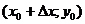 ,
, 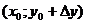 ,
, 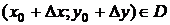 .
.
Определение. Частной производной функции  по переменной x в точке
по переменной x в точке  называется предел отношения частного приращения функции z по переменной x в точке
называется предел отношения частного приращения функции z по переменной x в точке  к приращению аргумента
к приращению аргумента 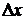 , когда
, когда 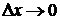 .
. 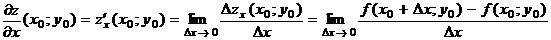 .
.
Определение. Частной производной функции  по переменной y в точке
по переменной y в точке  называется предел отношения частного приращения функции z по переменной y в точке
называется предел отношения частного приращения функции z по переменной y в точке  к приращению аргумента y, когда
к приращению аргумента y, когда 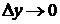 .
.
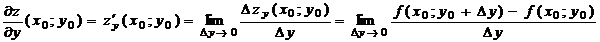 .
.
Замечание: 1) все правила дифференцирования функции одной переменной справедливы для функций многих переменных; 2) при нахождении частной производной функции по одной переменной все остальные переменные считают постоянными, то есть для функции  при вычислении
при вычислении 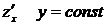 , при вычислении
, при вычислении 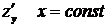 ; для функции
; для функции  при вычисления
при вычисления 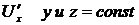 , при вычислении
, при вычислении 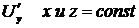 , при вычислении
, при вычислении 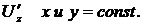
Пример.
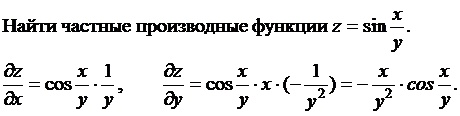
Градиент функции
Градиент функции.
Определение. Градиентом функции  в точке
в точке  называется вектор с координатами равными частным производным функции z в точке
называется вектор с координатами равными частным производным функции z в точке  и обозначается
и обозначается  .
.
Градиент функции указывает направление наискорейшего роста функции, а максимальная скорость роста функции равна модулю градиента.
Скалярное произведение  равно производной функции по направлению
равно производной функции по направлению  в точке
в точке  . Действительно
. Действительно 
 Величина в правой части принимает наибольшее значение при
Величина в правой части принимает наибольшее значение при  , т.е. когда
, т.е. когда  совпадает по направлению с
совпадает по направлению с  . В свою очередь частные производные функции
. В свою очередь частные производные функции  и
и  является производными функции z в направлении координатных осей OX и OY.
является производными функции z в направлении координатных осей OX и OY.
 ;
;
 .
.
Метод наименьших квадратов
Метод наименьших квадратов.
Рассмотрим систему линейных уравнений (1)  Предположим, что система (1) является результатом исследования, а вектор
Предположим, что система (1) является результатом исследования, а вектор  – результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?
– результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?
Случаи, когда  удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что
удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что  не опровергает теорию, если является хотя бы примерным решением системы (1). В таком случае разность
не опровергает теорию, если является хотя бы примерным решением системы (1). В таком случае разность  – является
– является  ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов:
ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов:
1. 
2. 
3.  .
.
Алгоритм поиска наименьшего значения функции  , то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.
, то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.
Определение неопределенного интеграла и его основные свойства. Таблица неопределенных интегралов элементарных функций.
Несобственный интеграл
Несобственные интегралы.
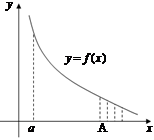 Рассмотрим
Рассмотрим 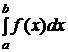 . Функция
. Функция  определена на конечном промежутке
определена на конечном промежутке 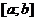 и ограничена на нем. Если нарушается хотя бы одно из двух требований, то мы имеем дело с несобственным интегралом.
и ограничена на нем. Если нарушается хотя бы одно из двух требований, то мы имеем дело с несобственным интегралом.
1. Пусть нарушается требование конечности чисел a и (или) b. При этом возможны случаи:
1) пусть  определена на
определена на 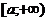 и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке 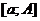 , где
, где 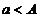 .
.
Несобственным интегралом первого рода называется 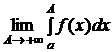 и обозначается
и обозначается 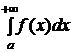 , то есть
, то есть 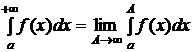 (1).
(1).
Если предел в правой части равенства (1) существует и конечен, то несобственный интеграл называется сходящимся и его значение равно пределу правой части. В противном случае несобственный интеграл называется расходящимся.
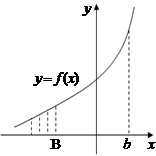 2) пусть
2) пусть  определена на
определена на 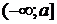 и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке 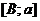 ,
, 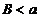
Несобственный интеграл первого рода в этом случае определяется по формуле 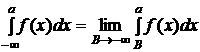 (2).
(2).
3) пусть  определена на
определена на 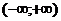 и интегрируема на каждом конечном отрезке этого интервала, тогда
и интегрируема на каждом конечном отрезке этого интервала, тогда 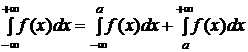 (3), причем несобственный интеграл в левой части называется сходящимся, если сходятся оба интеграла в правой части равенства (3). Если хотя бы один из них расходится, то расходится интеграл в левой части.
(3), причем несобственный интеграл в левой части называется сходящимся, если сходятся оба интеграла в правой части равенства (3). Если хотя бы один из них расходится, то расходится интеграл в левой части.
Замечание. Если 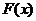 первообразная функции
первообразная функции  на
на 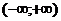 , тогда справедлива обобщенная формула Ньютона-Лейбница
, тогда справедлива обобщенная формула Ньютона-Лейбница 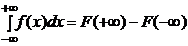 , где
, где 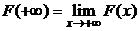 ,
, 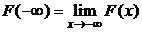 .
.
Пример. 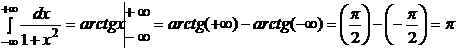
2. Пусть нарушается требование ограниченности функции  .
.
1) Пусть функция 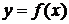 непрерывна на
непрерывна на 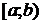 и
и 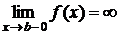 , тогда
, тогда 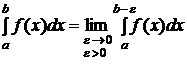 (4).
(4).
2) Если 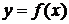 непрерывна на
непрерывна на  и
и 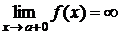 , тогда
, тогда 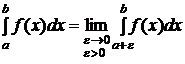 (5).
(5).
Интегралы в левой части равенств (4) и (5) называются сходящимися, если в правой части этих равенств предел существует и конечен и значение несобственного интеграла равно пределу правой части. Если в правой части равенств (4) и (5) пределы не существуют или бесконечны, то несобственные интегралы в левой части этих формул называются расходящимися.
 3) Если
3) Если 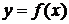 непрерывна на
непрерывна на 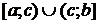 и
и 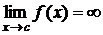 , тогда
, тогда 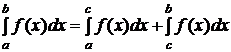 (6).
(6).
Интеграл в левой части равенства (6) называется сходящимся, если сходятся оба интеграла в правой части этой формулы; и расходящимся, если расходится хотя бы один из интегралов в правой части этой формулы.
Пример. Установить сходимость интеграла 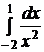 .
.
Так как 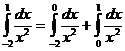 и
и 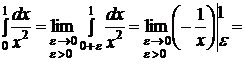
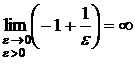 , то есть
, то есть
