Сопротивление материалов - наука о прочности и деформируемости материалов и элементов машин и сооружений.
В СМ считают, что материал материал любого тела представляет собой сплошную среду и обладает одинаковыми физико – механическими свойствами во всех точках тела.
Деформация, исчезающая после прекращения действия внешних сил, называется упругой; деформация, не исчезающая после прекращения действия внешних сил, называется остаточной или пластической.
В сопромате выполняют три вида расчетов: на прочность, жесткость и устойчивость.
Прочность – способность конструкции сопротивляться действию внешних сил, не разрушаясь (возникновение значительных остаточных деформаций также считается нарушением прочности).
Расчеты на прочность дают возможность определить размеры и форму деталей, выдерживающих заданную нагрузку, при наименьшей затрате материала.
Жесткость – способность конструкции сопротивляться деформациям.
Расчеты на жесткость гарантируют, что изменения формы и размеров конструкций не превысят допустимых норм.
Устойчивость – способность конструкции сопротивляться силам стремящимся вывести ее из исходного состояния равновесия.
Расчеты на устойчивость предотвращают возможность внезапной потери устойчивости и искривления длинных или тонких деталей.
3. Основным расчетным элементом в сопротивлении материалов является брус.
В зависимости от их назначения в конструкции брусья называют колоннами, балками, стержнями.
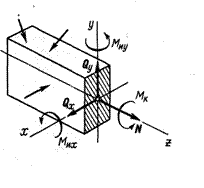Оси Х,У – поперечные оси; ось Z — продольная ось;
Нагрузки, действующие на конструкции, бывают сосредоточенными или распределенными.
В зависимости от характера действия нагрузки подразделяют на статические и динамические.
Статическими называются нагрузки, числовое значение, направление и место приложения которых остаются постоянными или меняются медленно и незначительно. Пример статической нагрузки — сила тяжести сооружений.
Динамическими называются нагрузки, характеризующиеся быстрым изменением во времени их значения, направления или места приложения.
5. Из практики известно, что в процессе эксплуатации элементы конструкций испытывают следующие основные деформации:
растяжение, сжатие, сдвиг (сдвиг, доведенный до разрушения материала, называют срезом), кручение, изгиб.
Метод сечений.
Для расчетов деталей машин и сооружений на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.
Метод сечений заключается в том, что тело мысленно разрезается плоскостью на две части, любая из которых отбрасывается и взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза; оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Если внешние силы, действующие на брус, представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (см. рис.), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно: åC=0, åU=0, åZ=0, åMх=0, åMy=0, åMz=0.
Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия:
N — продольная сила,
Qx, Qy — поперечные силы,
Мz — крутящий момент,
М х, М у — изгибающие моменты.
При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи:
1. В сечении возникает только продольная сила N. В этом случае это деформация растяжения (если сила N направлена от сечения) или деформация сжатия (если сила N направлена к сечению).
2. В сечении возникает только поперечная сила Q – деформация сдвига (среза).
3. В сечении возникает только крутящий момент Мz – деформация кручения.
4. В сечении возникает только изгибающий момент Мx (Мy) – чистый изгиб.
Напряжение.
Напряжение характеризует интенсивность внутренних сил, действующих в сечении.
Напряжение – внутренняя сила, отнесенная к единице площади сечения.
Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу, а именно мегапаскаль (МПа):
1 Мпа = 106 Па = 1 Н/мм2.
Напряжение – величина векторная.
Разложим вектор напряжения rна две составляющие:
s — перпендикулярную плоскости сечения (нормальное напряжение) и
t — лежащую в плоскости сечения (касательное напряжение).
Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения rопределится по формуле: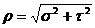 
8. Принцип независимости действия сил:
при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.
ТЕМА 2. РАСТЯЖЕНИЕ (СЖАТИЕ)
Растяжение (сжатие) – деформация прямого бруса (стержня) при которой в любом поперечном сечении бруса возникает только продольная сила N и изменяется длина бруса.
Внешние силы, направленные от торцевого сечения бруса – растягивающие – « + ».
Силы, направленные к сечению – сжимающие – « ― ».
Продольная сила N в произвольном сечении бруса численно равна алгебраической сумме проекций на ось Z всех внешних сил оставшейся части бруса: N = ΣFi ост. части
При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле: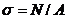 
[Н/мм² = МПа]
где N — продольная сила; А — площадь поперечного сечения.
Эпюра – график, наглядно показывающий изменение продольных сил и напряжений по длине бруса.
Правила решения построения эпюр:
1. Ось Z направляем от жесткой заделки;
2. Брус разбиваем на участки, границами которых являются точки приложения внешних сил и места изменений площади поперечных сечений;
3. Нумеруем участки и начинаем решение со свободного конца бруса;
4. Определяем продольную силу N на каждом участке, пользуясь методом сечений;
5. Определяем напряжения на каждом из участков: 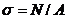, Н/мм²
6. Строим эпюры N и σ. Построение проводим в масштабе, исходя из удобства построения.
Правило контроля: В месте приложения внешней силы на эпюре N должен быть скачок на величину приложенной силы.