Автор: преподаватель Оксанич Л. В.

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

КРАТКИЙ КУРС ЛЕКЦИЙ

Автор: преподаватель Оксанич Л. В.

СОДЕРЖАНИЕ

1. Тема 1. Основные положения 3

2. Тема 2. Растяжение ( сжатие) 5

3. Тема 3. Смятие, срез 7

4. Тема 4. Геометрические характеристики сечений 8

5. Тема 5. Кручение 9

6. Тема 6. Изгиб 11

7. Тема 7. Устойчивость сжатых стержней 13

8. Тема 8. Сочетание деформаций 15

9. Тема 9. Сопротивление усталости 16

ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ СОПРОМАТА

Сопротивление материалов - наука о прочности и деформируемости материалов и элементов машин и сооружений.

В СМ считают, что материал материал любого тела представляет собой сплошную среду и обладает одинаковыми физико – механическими свойствами во всех точках тела.

Деформация, исчезающая после прекращения действия внешних сил, называется упругой; деформация, не исчезающая после прекращения действия внешних сил, называется остаточной или пластической.

В сопромате выполняют три вида расчетов: на прочность, жесткость и устойчивость.

Прочность – способность конструкции сопротивляться действию внешних сил, не разрушаясь (возникновение значительных остаточных деформаций также считается нарушением прочности).

Расчеты на прочность дают возможность определить размеры и форму деталей, выдерживающих заданную нагрузку, при наименьшей затрате материала.

Жесткость – способность конструкции сопротивляться деформациям.

Расчеты на жесткость гарантируют, что изменения формы и размеров конструкций не превысят допустимых норм.

Устойчивость – способность конструкции сопротивляться силам стремящимся вывести ее из исходного состояния равновесия.

Расчеты на устойчивость предотвращают возможность внезапной потери устойчивости и искривления длинных или тонких деталей.

3. Основным расчетным элементом в сопротивлении материалов является брус.

В зависимости от их назначения в конструкции брусья называют колоннами, балками, стержнями.

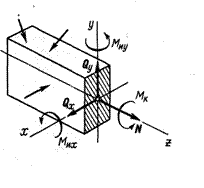Оси Х,У – поперечные оси; ось Z — продольная ось;

Нагрузки, действующие на конструкции, бывают сосредоточенными или распределенными.

В зависимости от характера действия нагрузки подразделяют на статические и динамические.

Статическими называются нагрузки, числовое значение, направление и место приложения которых остаются постоянными или меняются медленно и незначительно. Пример статической нагрузки — сила тяжести сооружений.

Динамическими называются нагрузки, характеризующиеся быстрым изменением во времени их значения, направления или места приложения.

5. Из практики известно, что в процессе эксплуатации элементы конструкций испытывают следующие основные деформации:

растяжение, сжатие, сдвиг (сдвиг, доведенный до разрушения материала, называют срезом), кручение, изгиб.

Метод сечений.

Для расчетов деталей машин и сооружений на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.

Метод сечений заключается в том, что тело мысленно разрезается плоскостью на две части, любая из которых отбрасывается и взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза; оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.

Если внешние силы, действующие на брус, представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (см. рис.), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно: åC=0, åU=0, åZ=0, åM_х=0, åM_y=0, åM_z=0.

Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия:

N — продольная сила,

Q_x, Q_y — поперечные силы,

М_z — крутящий момент,

М _х, М _у — изгибающие моменты.

При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи:

1. В сечении возникает только продольная сила N. В этом случае это деформация растяжения (если сила N направлена от сечения) или деформация сжатия (если сила N направлена к сечению).

2. В сечении возникает только поперечная сила Q – деформация сдвига (среза).

3. В сечении возникает только крутящий момент М_z – деформация кручения.

4. В сечении возникает только изгибающий момент М_x (М_y) – чистый изгиб.

Напряжение.

Напряжение характеризует интенсивность внутренних сил, действующих в сечении.

Напряжение – внутренняя сила, отнесенная к единице площади сечения.

Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу, а именно мегапаскаль (МПа):

1 Мпа = 10⁶ Па = 1 Н/мм².

Напряжение – величина векторная.

Разложим вектор напряжения rна две составляющие:

s — перпендикулярную плоскости сечения (нормальное напряжение) и

t — лежащую в плоскости сечения (касательное напряжение).

Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения rопределится по формуле: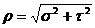

8. Принцип независимости действия сил:

при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.

ТЕМА 2. РАСТЯЖЕНИЕ (СЖАТИЕ)

Растяжение (сжатие) – деформация прямого бруса (стержня) при которой в любом поперечном сечении бруса возникает только продольная сила N и изменяется длина бруса.

Внешние силы, направленные от торцевого сечения бруса – растягивающие – « + ».

Силы, направленные к сечению – сжимающие – « ― ».

Продольная сила N в произвольном сечении бруса численно равна алгебраической сумме проекций на ось Z всех внешних сил оставшейся части бруса: N = ΣFi _{ост. части}

При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле: 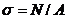[Н/мм² = МПа]

где N — продольная сила; А — площадь поперечного сечения.

Эпюра – график, наглядно показывающий изменение продольных сил и напряжений по длине бруса.

Правила решения построения эпюр:

1. Ось Z направляем от жесткой заделки;

2. Брус разбиваем на участки, границами которых являются точки приложения внешних сил и места изменений площади поперечных сечений;

3. Нумеруем участки и начинаем решение со свободного конца бруса;

4. Определяем продольную силу N на каждом участке, пользуясь методом сечений;

5. Определяем напряжения на каждом из участков: 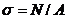, Н/мм²

6. Строим эпюры N и σ. Построение проводим в масштабе, исходя из удобства построения.

Правило контроля: В месте приложения внешней силы на эпюре N должен быть скачок на величину приложенной силы.

Удлинение стержня

Подставив в формулу закона Гука значения нормального напряжения σ = N/A и продольной деформации ε =Δ l / l, получим N / A = EΔl /l, откуда определим изменение длины стержня Δl = N l / E A,мм,

где l – длина участка бруса, мм, A – площадь поперечного сечения участка бруса, мм²

Перемещения поперечных сечений балки l определяются как сумма удлинений (укорочений) Δl участков бруса, расположенных между жесткой заделкой и данным сечением. Перемещение сечения, расположенного в жесткой заделке = 0.

График изменения перемещений стержня вдоль его оси называется эпюрой перемещений.

Три категории напряжений

1. Расчетные – определяются расчетом ,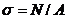

2. Предельные (опасные) – при которых образец разрушается.

Для пластичных материалов – σ_т ; для хрупких – σ_в;

3. Допускаемые – наибольшие напряжения, которые можно допустить в данной

конструкции – [σ ]. [σ ] = σ _пред/ [n],

где [n] – нормативный коэффициент запаса прочности.

Расчеты на прочность

1. Проверочный расчет s_max = N _max / A £ [s]

2. Проектный расчет А ≥ N _max / [σ ]

3. Определение допускаемой нагрузки .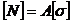

ТЕМА 3. СМЯТИЕ

Если детали конструкции, передающие значительную сжимающую нагрузку, имеют небольшую площадь контакта, то может произойти смятие поверхностей деталей. При этом возникают нормальные напряжения смятия, равномерно распределенные по площади контакта.

Расчетное уравнение на смятие имеет вид: ,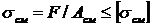

где F—сжимающая сила; [s_см] — допускаемое напряжение на смятие; А_см — площадь контакта.

Для болтовых, штифтовых и шпоночных соединений из низкоуглеродистой стали [s_см] = 100... 120 МПа, для клепаных соединений [s_см] = 240...320 МПа.

СДВИГ (СРЕЗ)

Сдвигом называется такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила Q. Сдвиг, доведенный до разрушения – срез.

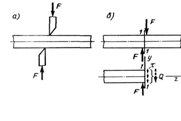
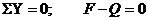, Q = F.

При сдвиге в поперечном сечении бруса действуют только касательные напряженияt = Q/A.

ОСЕВОЙ МОМЕНТ ИНЕРЦИИ

Понятие об осевых моментах инерции понадобится нам в дальнейшем при изучении теории изгиба.

Осевым моментом инерции плоской фигуры относительно оси называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат их расстояний до этой оси(рис.1).

Осевой момент инерции обозначим I с индексом, соответствующим оси:

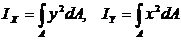; [м⁴, мм⁴].

Сложим моменты инерции относительно двух взаимно перпендикулярных осей х и у (рис. 1.):

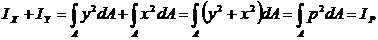, т.е.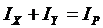

Момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру.

Осевые моменты инерции некоторых простых фигур:

· Прямоугольник b´ h (рис. 2). ,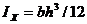

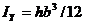
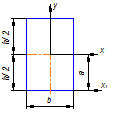
Рис.2

· Круг диаметром d относительно осей х и у. В силу симметрии для круга I_Х = I_У.Так как 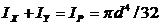, то .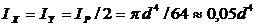

· Осевые моменты для стандартных профилей определяются по справочным таблицам.

3. ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.

Оси, относительно которых моменты инерции имеют максимальное и минимальное значения, называются главными осями инерции.

Момент инерции относительной главной оси называется главным моментом инерции.

Если главная ось проходит через центр тяжести фигуры, то она называется главной центральной осью, а момент инерции относительно этой оси — главным центральным моментом инерции. Если фигура имеет ось симметрии, то эта ось всегда будет одной из главных центральных осей.

ТЕМА 5. КРУЧЕНИЕ

Кручением называется такой вид деформации, при котором в поперечных сечениях бруса возникает только крутящий момент (М_К илиМ_z).

· Крутящий момент в произвольном поперечном сечении бруса определяют методом сечений, он равен алгебраической сумме внешних моментов, действующих на от­сеченную часть: M_k=SM_{i ост. части}.

· Внешние скручивающие моменты определяют по формуле:M = P/w,

где Р — передаваемая мощность, Вт; w — угловая скорость вращения вала, рад/с.

· Внешний скручивающий момент считаем положительным, если он направлен против часовой стрелки.

ТЕМА 6. ИЗГИБ

· Изгиб – такой вид деформации, при котором в любом поперечном сечении бруса возникает изгибающий момент М_и.

· Брус, работающий на изгиб – балка. На изгиб работают оси, валы и другие детали конструкций.

· Если все силы лежат в одной плоскости – изгиб называют плоским;

· Если в любом поперечном сечении бруса возникает только изгибающий момент – изгиб называют чистым;

· Изгиб, при котором в поперечном сечении балки возникают изгибающий момент и поперечная сила, называется поперечным.

· Если внешние силы перпендикулярны продольной оси балки, при этом силовая плоскость совпадает с плоскостью симметрии балки, то изгиб – прямой.

· Для определения внутренних силовых факторов пользуются методом сечений.

ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР ПРИ ИЗГИБЕ (СОСРЕДОТОЧЕННАЯ НАГРУЗКА)

1. Для участка, где отсутствует распределенная нагрузка, поперечная сила постоянна, а изгибающий момент меняется по линейному закону, т.е график М_и – наклонная линия.

2. В частном случае, когда поперечная сила на участке равна нулю, изгибающий момент постоянен, график М_и – прямая линия, параллельная оси z.

3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов – излом.

4. В сечении, где к балке приложена пара сил (момент), на эпюре М_и возникает скачок на величину момента. Поперечная сила при этом не изменяется.

5. На конце балки поперечная сила равна приложенной в этом сечении внешней силе.

6. На конце балки М_и равен нулю, за исключением случаев, когда в этом сечении приложен внешний момент. В этом случае М_и равен внешнему моменту.

7.

ПОСТРОЕНИЕ ЭПЮР Q и М

(ПРИЛОЖЕНЫ СОСРЕДОТОЧЕННЫЕ СИЛЫ И РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ)

1. Для участка балки с равномерно распределенной нагрузкой поперечная сила Q изменяется по линейному закону, т.е. эпюра Q – наклонная прямая линия.

2. Изгибающий момент изменяется по квадратичному закону, эпюра М_и –парабола, причем, если распределенная нагрузка направлена вниз, то парабола обращена выпуклостью наверх и наоборот.

3. В сечении, где эпюра пересекает ось , т.е Q = 0, М_и – экстремален.

РАСЧЕТЫ НА ПРОЧНОСТЬ

1.Проверочный расчет на прочность при изгибе: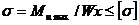

СПОСОБЫ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ СИЛЫ

РАСЧЕТ ПО ФОРМУЛЕ ЭЙЛЕРА

,

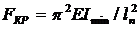где Е—модуль упругости ;

I_min — наименьший из осевых моментов инерции сечения (I_x или I_y ), поскольку искривление стержня происходит в плоскости наименьшей жесткости;

l_п — приведенная длина стержня; ,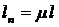

где l—длина стержня, m — коэффициент приведения длины, зависящий от способа закрепления концов стержня, иначе называемый коэффициентом заделки.

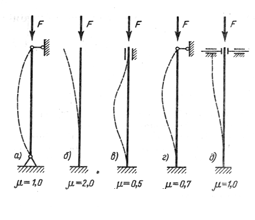
· На рис. показаны наиболее часто встречающиеся способы закрепления концов стержня и приведены значения m:

· Чем меньше m, тем больше критическая сила, а следовательно, и допускаемая сжимающая нагрузка.

· Поэтому там, где это возможно, следует осуществлять жесткое защемление обоих концов стержня.

Предел выносливости

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

КРАТКИЙ КУРС ЛЕКЦИЙ

Автор: преподаватель Оксанич Л. В.

СОДЕРЖАНИЕ

1. Тема 1. Основные положения 3

2. Тема 2. Растяжение ( сжатие) 5

3. Тема 3. Смятие, срез 7

4. Тема 4. Геометрические характеристики сечений 8

5. Тема 5. Кручение 9

6. Тема 6. Изгиб 11

7. Тема 7. Устойчивость сжатых стержней 13

8. Тема 8. Сочетание деформаций 15

9. Тема 9. Сопротивление усталости 16

ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ СОПРОМАТА