Определение оптимального выпуска продукции при многокритериальных экономических показателях

Фирма выпускает два вида изделий по цене 2 ден. ед. и 3 ден. ед. соответственно. По результатам маркетинговых ис­следований спрос на изделия второго вида не менее 1 тыс. ед. в год. Для производства изделий используются материалы А и В, запасы которых на фирме составляют 18 и 15 т соответ­ственно. Для изготовления 1 тыс. изделий норма расхода ма­териала А для изделий 1-го вида составляет 3 т, а для изделий 2-го вида — 5 т. Для изготовления 1 тыс. изделий материала В расходуется: для изделий 1-го вида — 5 т, для изделий 2-го вида — 3 т. Себестоимость изделий 1-го вида — 1 ден. ед., а 2-го вида — 2 ден. ед.

Найти оптимальное решение по производству изделий 1-го и 2-го видов, чтобы прибыль и количество выпускаемых изде­лий были максимальными, себестоимость минимальной.

Решение. Обозначим: x₁ — количество изделий 1-го вида, тыс. ед.; x₂ — количество изделий 2-го вида тыс. ед.

Математическая модель задачи будет иметь вид

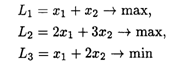
при ограничениях:

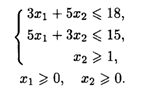
Решим задачу по каждой целевой функции в отдельности. Получим

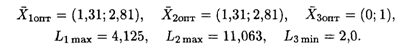
Математическая модель задачи нахождения компромиссно­го решения:

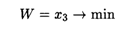
при ограничениях:

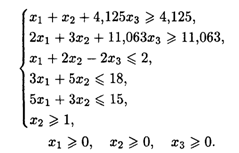
Решая задачу на ПЭВМ, получим

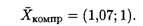
Таким образом, фирме целесообразно выпускать 1,07 тыс. изделий 1-го вида и 1 тыс. изделий 2-го вида.

УПРАЖНЕНИЯ

Составить математическую модель нахождения компромиссно­го решения и найти его.

27.1. L₁ = x₁ + 2x₂ → max, L₂ = 4x₁ + х₂ → min при ограни­чениях:

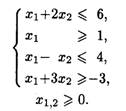
27.2. L₁ = 2x₁ + x₂ → max, L₂ = 2x₁ + x₂ → min при ограни­чениях:

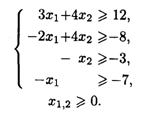
27.3. L₁ = x₁ + 3x₂ → max, L₂ = 2x₁ + x₂ → min при ограни­чениях:

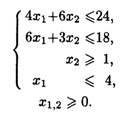
27.4. L₁ = 4x₁ + x₂ → max, L₂ = x₁ + 4x₂ → min при ограни­чениях:

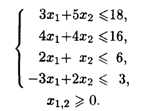
27.5. L₁ = x₁ + 3x₂ → max, L₂ = x₁ + x₂ → min при ограниче­ниях:

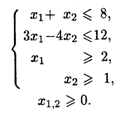
27.6. L₁ = 5x₁ +4x₂ → max, L₂ = x₂ → max при ограничениях:

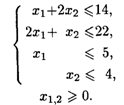
27.7. L₁ = x₁ - x₂ → max, L₂ = x₁ + 2x₂ → max, L₃ = 2x₁ + x₂ → min при ограничениях:

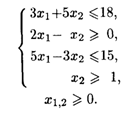
Часть 6. ЭЛЕМЕНТЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Глава 28. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Общая постановка задачи

Математическая модель задачи нелинейного программиро­вания в общем виде формулируется следующим образом: найти вектор = (х₁, x₂, …, x_n), удовлетворяющий системе ограни­чений

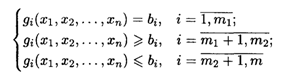
и доставляющий экстремум (наибольшее или наименьшее зна­чение) целевой функции

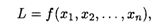
где x_j — переменные, j = 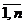; L, f, g_i — заданные функции от n переменных, b_i — фиксированные значения.

Нелинейное программирование применяется при прогнози­ровании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудова­ния и т.д.

Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программи­рование, градиентные методы, приближенные методы реше­ния, графический метод.

Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако даже для таких задач оптималь­ное решение может быть найдено для определенного класса це­левых функций. Например, когда целевая функция сепарабельная, т.е. является суммой п функций f_j(x_j), или квадратичная. При этом следует отметить, что в отличие от задач линейного программирования, где точками экстремума являются верши­ны многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине.

При решении задач нелинейного программирования для це­левой функции необходимо определить глобальный максимум или глобальный минимум. Глобальный максимум (минимум) функции — это ее наибольшее (наименьшее) значение из ло­кальных максимумов (минимумов).

Наличие локальных экстремумов затрудняет решение за­дач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найден­ный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять ло­кальный экстремум, который может существенно отличаться от глобального.

Графический метод

Рассмотрим примеры решения задач нелинейного програм­мирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и не­линейном виде. Так же как и в задачах линейного программи­рования, они могут быть решены графически.

Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы функции

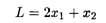
при ограничениях:

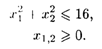
Решение. Область допустимых решений — часть окруж­ности с радиусом 4, которая расположена в первой четверти (рис. 28.1).

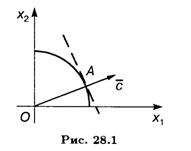
Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем че­рез точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение x₂ = 1/2х₁.

Решаем систему

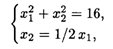
откуда находим х₁ = 8 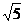/5, x₂ = 4 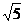/5, L = 16 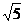/5 + 4 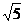/5 = 4 .

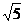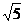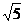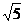Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4 , — в точке А(8 /5, 4 /5).

Задача с нелинейной целевой функцией и линейной системой ограничений

Пример 2. Найти глобальные экстремумы функции

при ограничениях:

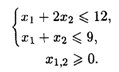
Решение. Область допустимых решений — OABD (рис. 28.2). Линиями уровня будут окружности с центром в

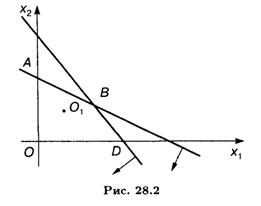
точке O₁. Максимальное значение целевая функция имеет в точке D(9, 0), минимальное — в точке O₁ (2, 3). Поэтому

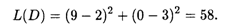
Ответ. Глобальный максимум, равный 58, достигается в точке D (9, 0), глобальный минимум, равный нулю, — в точке O₁ (2, 3).

Пример 3. Найти глобальные экстремумы функции

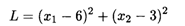
при ограничениях:

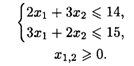
Решение. Область допустимых решений — OABD (рис. 28.3). Линии уровня представляют собой окружности с центром в точке O₁ (6, 3). Глобальный максимум находится в точке O (0, 0) как самой удаленной от точки O₁. Глобальный минимум расположен в точке Е, находящейся на пересечении прямой 3x₁ + 2x₂ = 15 и перпендикуляра к этой прямой, про­веденного из точки O₁.

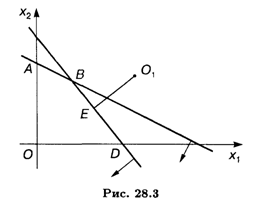
Найдем координаты точки Е: так как угловой коэффици­ент прямой 3x₁ + 2x₂ = 15 равен -3/2, то угловой коэффициент перпендикуляра O₁Е равен 2/3. Из уравнения прямой, прохо­дящей через данную точку О₂ с угловым коэффициентом 2/3, получим

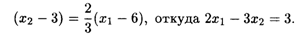
Решая систему

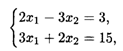
находим координаты точки Е: х₁ = 51/13, x₂ = 21/13, при этом L(Е) = 1053/169.

Координаты точки Е можно найти следующим образом: дифференцируя выражение (x₁ — 6)² + (x₂ - 3)² как неявную функцию по x₁, получим

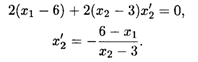
Приравниваем полученное значение к тангенсу угла накло­на прямой 3x_­1 + 2x₂ = 15:

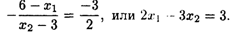
Решаем систему уравнений

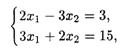
получим координаты точки Е: х₁ = 51/13, x₂ = 21/13.

Ответ. Глобальный максимум, равный 52, находится в точке O (0, 0). Глобальный минимум, равный 1053/169, нахо­дится в точке E (51/13, 21/13).

Задача с нелинейной целевой функцией и нелинейной системой ограничений

Пример 4. Найти глобальные экстремумы функции

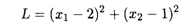
при ограничениях:

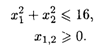
Решение. Областью допустимых решений является ок­ружность с радиусом 4, расположенная в первой четверти (рис. 28.4). Линиями уровня будут окружности с центром в точке O₁ (2, l).

Глобальный минимум достигается в точке O₁. Глобальный максимум — в точке А (0, 4), при этом

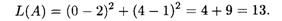
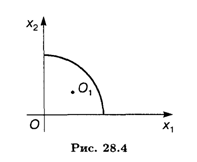
Ответ. Глобальныи минимум, равный нулю, достигается в точке O₁ (2, l), глобальный максимум, равный 13, находится в точке А (0, 4).

Пример 5. Найти глобальные экстремумы

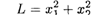
при ограничениях:

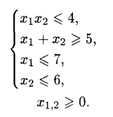
Решение. Область допустимых решений не является вы­пуклой и состоит из двух частей (рис. 28.5). Линиями уровня являются окружности с центром в точке O (0, 0).

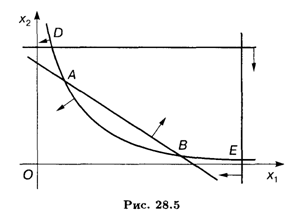
Найдем координаты точек А и В, решая систему

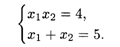
Получим А (1, 4), В (4, 1). В этих точках функция имеет гло­бальные минимумы, равные 17. Найдем координаты точек D и Е, решая системы

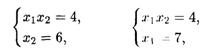
откуда получаем D (2/3, 6) и L(D) = 328/9, E (7, 4/7) и L(E) = 2417/49.

Ответ. Целевая функция имеет два глобальных миниму­ма, равных 17, в точках А (1, 4) и B (4, 1), глобальный макси­мум, равный 2417/49, достигается в точке E (7, 4/7).