Выбор инвестиционных проектов в условиях ограниченности финансовых ресурсов

При планировании вложений проект может быть принят к исполнению, если он имеет положительную чистую приведен­ную стоимость. Однако в действительности для предприятий существуют ограничения, связанные с нехваткой финансовых ресурсов на его осуществление. В этом случае возникает не­обходимость разработки такого метода отбора одного проекта (или группы проектов), который, с одной стороны, обеспечит максимально возможную чистую приведенную стоимость, а с другой — позволит "уложиться" в выделенные для инвестиций средства.

Например, у предприятия для выполнения некоторых про­грамм имеется пять инвестиционных проектов, чистая приве­денная стоимость которых указана в табл. 26.2. Однако пред­приятие не может финансировать все проекты: суммы денег, выделенные на текущий год и последующие два, меньше не­обходимых для инвестирования в полном объеме. При этом оставшиеся денежные средства не могут быть перенесены на следующие годы, также не предусмотрено более одного финан­сирования одного и того же проекта. Требуется распределить выделенные средства в инвестиционные проекты оптимальным способом.

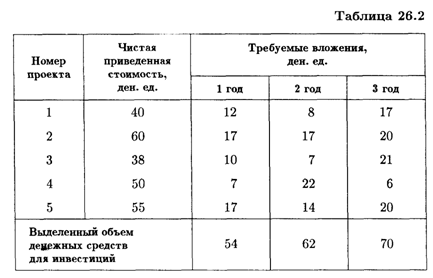
Решение. Обозначим черех x_j долю вложения в j-й про­ект, где j = 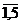. Тогда чистая приведенная стоимость инвес­тиций в 1-й проект составит 40x₁; во 2-й проект — 60x₂ и т.д. При этом необходимо учитывать, что инвестиции не должны превышать 54, 62 и 70 ден. ед. в первый, второй и третий годы соответственно. Требуется выбрать один или группу проектов с наибольшей совокупной чистой приведенной стоимостью.

Математическая модель этой экономической задачи имеет вид

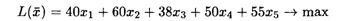
при ограничениях:

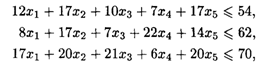
причем x_j = 0 или 1, j = 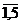(проект либо финансируется, либо нет).

Решая задачу на компьютере, получаем х₁ = х₂ = х₄= x₅ = 1, x₃ = 0. Иными словами, необходимо производить финансирование 1, 2, 4 и 5-го проектов. При этом потребуются денежные средства в объеме 177 ден. ед. в течение трех лет (при выделяемом предприятием объеме 186 ден. ед.), а сумма чистой приведенной пои мести проектов будет максимальной и составит 205 ден. ед.

Математическая модель может быть составлена для произ­вольного конечного числа программ при предполагаемом фи­нансировании в течение любого количества лет.

УПРАЖНЕНИЯ

26.1. Фирма имеет три механизма A₁, А₂, А₃, каждый из ко­торых может быть использован на каждом из трех видов ра­бот B₁, B₂, B₃с производительностью, заданной матрицей (в условных единицах)

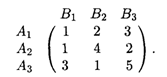
Распределить механизмы по одному на каждую из работ так, чтобы суммарная производительность всех механизмов была максимальной.

26.2. Пять человек должны выполнить четыре работы, при­чем каждый из работников с разной производительностью мо­жет выполнить любую из этих работ. Предусматривается, что каждый работник в состоянии сделать только одну работу.

Производительности работников при выполнении работ зада­ны матрицей

Распределить людей на работу так, чтобы выполнить ее с мак­симальной производительностью.

26.3. Фирма, имеющая четыре склада, получила четыре зака­за, которые необходимо доставить различным потребителям. Складские помещения каждой базы имеют вполне достаточ­ное количество товара, чтобы выполнить любой один из этих заказов.

Расстояния между каждой базой и каждым потребителем приведены в матрице

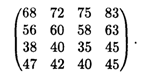
Как следует распределить заказы по базам, чтобы общая даль­ность транспортировки была минимальной?

26.4. Фирма объединяет три предприятия, каждое из которых производит 3 вида изделий.

Себестоимости каждого изделия в усл. ед. при изготовле­нии на каждом предприятии указаны в матрице

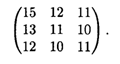
Учитывая необходимость специализации каждого предприятия только по одному изделию, распределить производство изде­лий по предприятиям так, чтобы изделия имели минимальную себестоимость.

26.5. Компания разрабатывает план выпуска трех новых ви­дов продукции. Она уже владеет пятью предприятиями, и те­перь на трех из них должны производиться новые виды про­дукции — по одному виду на одно предприятие.

Даны издержки производства единицы продукции, усл. ед.:

Издержки сбыта единицы продукции, усл. ед.:

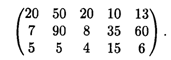
Плановый объем годового производства, который позволил бы удовлетворить спрос, и себестоимость единицы продукции каждого вида приведены в табл. 26.3.

Закрепить выпуск продукции между предприятиями, обеспе­чивающий получение наибольшей прибыли за год.