Глава 26. задача о назначениях

Постановка задачи

Задача заключается в выборе такого распределения ре­сурсов по объектам, при котором минимизируется стоимость назначений. Предполагается, что каждый ресурс назначается ровно один раз и каждому объекту приписывается ровно один ресурс.

Возможные применения задачи о назначениях представле­ны в табл. 26.1.

Матрица стоимостей С имеет вид

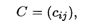
где c_ij — затраты, связанные с назначением i-го ресурса на j-й объект, i = j = 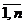, где п — число объектов или ресурсов.

Обозначим:

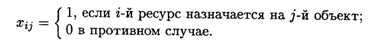
Таким образом, решение задачи может быть записано в ви­де Х = (x_ij).

Допустимое решение называется назначением. Оно строит­ся путем выбора ровно одного элемента в каждой строке мат­рицы X = (x_ij) и ровно одного элемента в каждом столбце этой матрицы.

Элементы c_ij матрицы С, соответствующие элементам x_ij = 1 матрицы X, будем отмечать кружками:

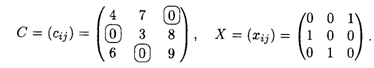
Математическая постановка задачи:

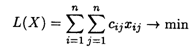
при ограничениях:

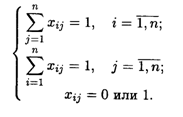
Алгоритм решения задачи

Задача о назначениях является частным случаем транспо­ртной задачи, в которой a_i = b_j = 1. Поэтому ее можно решать алгоритмами транспортной задачи. Рассмотрим другой метод, который является более эффективным, учитывающим специ­фику математической модели. Этот метод называется венгер­ским алгоритмом. Он состоит из следующих шагов:

1) преобразования строк и столбцов матрицы;

2) определение назначения;

3) модификация преобразованной матрицы.

1-й шаг. Цель данного шага — получение максимально воз­можного числа нулевых элементов в матрице С. Для этого из всех элементов каждой строки вычитаем ми­нимальный элемент соответствующей строки, а из всех элементов каждого столбца вычитаем минимальный эле­мент соответствующего столбца.

2-й шаг. Если после выполнения 1-го шага в каждой строке и каждом столбце матрицы С можно выбрать по одному нулевому элементу, то полученное решение будет опти­мальным назначением.

3-й шаг. Если допустимое решение, состоящее из нулей, не найдено, то проводим минимальное число прямых че­рез некоторые столбцы и строки так, чтобы все нули оказались вычеркнутыми. Выбираем наименьший невы­черкнутый элемент. Этот элемент вычитаем из каждого невычеркнутого элемента и прибавляем к каждому эле­менту, стоящему на пересечении проведенных прямых.

Если после проведения 3-го шага оптимальное решение не достигнуто, то процедуру проведения прямых следует повто­рять до тех пор, пока не будет получено допустимое решение.

Пример.

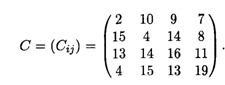
Распределить ресурсы по объектам.

Решение.1-й шаг. Значения минимальных элементов строк 1, 2, 3 и 4 равны 2, 4, 11 и 4 соответственно. Вы­читая из элементов каждой строки соответствующее ми­нимальное значение, получим

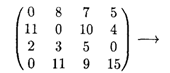
Значения минимальных элементов столбцов 1, 2, 3 и 4 равны 0, 0, 5, 0 соответственно. Вычитая из элементов каждого столбца соответствующее минимальное значе­ние, получим

2-й шаг. Ни одно полное назначение не получено, необходимо провести модификацию матрицы стоимостей.

3-й шаг. Вычеркиваем столбец 1, строку 3, строку 2 (или столбец 2). Значение минимального невычеркнутого эле­мента равно 2:

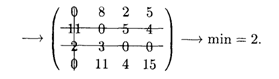
Вычитаем его из всех невычеркнутых элементов и, складывая его со всеми элементами, расположенными на пересечении двух линий, получим

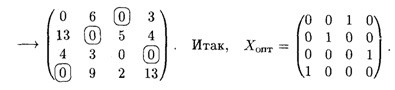
Ответ. Первый ресурс направляем на 3-й объект, вто­рой — на 2-й объект, четвертый — на 1-й объект, третий ре­сурс — на 4-й объект. Стоимость назначения: 9 + 4 + 11 + 4 = 28.

Примечания. 1. Если исходная матрица не является квад­ратной, то нужно ввести фиктивные ресурсы или фиктивные объекты, чтобы матрица стала квадратной.

2. Если какой-либо ресурс не может быть назначен на ка­кой-то объект, то соответствующая стоимость полагается рав­ной достаточно большому числу М.

3. Если исходная задача является задачей максимизации, то все элементы матрицы С следует умножить на (—1) и сло­жить их с достаточно большим числом так, чтобы матрица не содержала отрицательных элементов. Затем задачу следу­ет решать как задачу минимизации.

4. Если число линий, необходимое для того, чтобы вы­черкнуть нулевые элементы, равно числу строк или столб­цов (квадратной матрицы), то существует назначение нулевой стоимости.

Планирование загрузки оборудования с учетом максимальной производительности станков

Рассмотрим следующую задачу.

На предприятии пять станков различных видов, каждый из которых может выполнять пять различных операций по обра­ботке деталей. Известна производительность каждого станка при выполнении каждой операции, заданная матрицей

Определить, какую операцию и за каким станком следует за­крепить, чтобы суммарная производительность была макси­мальной при условии, что за каждым станком закреплена толь­ко одна операция.

Решение. Так как в задаче требуется определить max, a алгоритм метода дан для задач на min, умножим матрицу С на (—1). Сложим полученную матрицу, имеющую отрицатель­ные коэффициенты, с положительным числом, например с чис­лом 10. Получим

Минимальные элементы в строчках есть 3, 4, 4, 6, 4. Выч­тем их из соответствующих элементов матрицы, получим

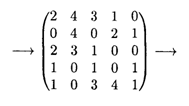
Так как назначение не получено, вычеркиваем строку 2, столбцы 2, 4, 5:

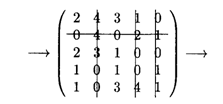
Минимальный элемент равен 1. Вычитаем его из всех не­вычеркнутых элементов и складываем со всеми элементами, расположенными на пересечении двух линий. Получаем

Оптимальное решение, соответствующее последней матри­це, равно

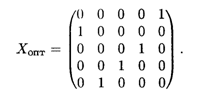
Суммарная производительность: 6 + 6 + 3 + 6 + 7= 28.

Таким образом, на первом станке надо делать 5-ю опера­цию, на втором — 1-ю операцию, на третьем — 4-ю операцию, на четвертом — 3-ю операцию, на пятом станке — 2-ю опе­рацию. Суммарная производительность: 28 деталей в единицу времени.