Экономический анализ транспортных задач
Проведем экономический анализ задачи на конкретном примере.
Пример 3. Три торговых склада могут поставлять некоторое изделие в количестве 9, 4 и 8 т. Величины спроса трех магазинов розничной торговли на это изделие равны 3, 5 и 6 т.
Какова минимальная стоимость транспортировки от поставщиков к потребителям? Провести анализ решения при условии, что единичные издержки транспортировки в усл. ед. даны в матрице
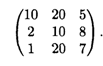
Решение. Запасы складов: 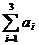 = 21 т, потребности магазинов:
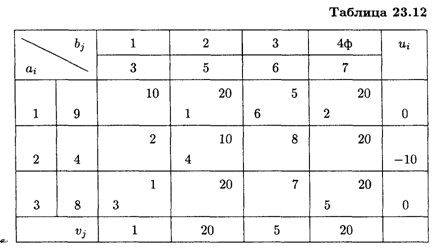
= 21 т, потребности магазинов: 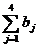 = 14 т, имеем открытую задачу. Введем фиктивный магазин со спросом b4ф = 7 т и тарифом 20 усл. ед. (табл. 23.12).
= 14 т, имеем открытую задачу. Введем фиктивный магазин со спросом b4ф = 7 т и тарифом 20 усл. ед. (табл. 23.12).
Оценки свободных клеток:
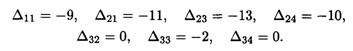
Оценки Δ32 = Δ34 = 0, задача имеет альтернативный оптимум, и одно из решений имеет вид
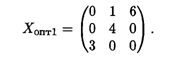
Минимальная стоимость транспортных расходов
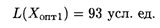
Итоговое распределение перевозок, а также значения оценок свободных клеток, которые называют теневыми ценами, можно использовать при проведении экономического анализа. Теневая цена показывает, на сколько увеличится общая стоимость транспортных расходов, если в пустую клетку поместить одно изделие. Например, если придется осуществить перевозку одного изделия с торгового склада 2 в розничный магазин 3, то увеличение стоимости составит |Δ23| = | - 13| = 13 усл. ед., что больше, чем тариф груза клетки (2,3), равный 8 усл. ед. Дополнительное увеличение стоимости транспортных расходов появляется в связи с перераспределением перевозок. Составим цикл распределения перевозок с помещением груза в пустую клетку (2, 3):
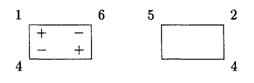
В клетку (2, 3) помещаем груз 4 т, в (1, 3) вместо 1т — 5т, в (2, 2) вместо 4т — пустая клетка.
Изменение расходов составит 4 ∙ 20 – 4 ∙ 10 + 8 ∙ 4 – 4 ∙ 5 = 72 усл. ед. или на одно изделие 72 : 4 = 13 усл. ед.
Если теневая цена клетки равна нулю (Δ32 = 0), то задача имеет альтернативный оптимум. Перераспределим грузы относительно клетки (3, 2):
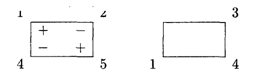
Еще одно оптимальное решение задачи имеет вид
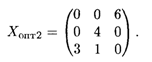
Минимальная стоимость транспортных расходов
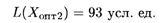
Аналогичный анализ можно провести и по остальным свободным клеткам.
Теневые цены свободных клеток можно использовать в качестве индикаторов изменений стоимости транспортировки одного изделия или тарифа.
Например, теневая цена пустой клетки (3, 3) равна |Δ33| = | - 2| = 2, а фактическая цена транспортировки одного изделия — 7 усл. ед. Следовательно, для того чтобы использование данной клетки в распределении перевозок привело к снижению общих транспортных расходов, нужно, чтобы тариф этой клетки был не более 7 – 2 = 5 усл. ед.
Проведем стоимостный анализ изменений в занятых клетках. При снижении тарифа увеличение числа изделий в данной клетке выгодно. Если же тарифы занятых клеток возрастают, то при достижении ими определенного значения использование этой клетки является нежелательным и необходимо произвести перераспределение грузов.
В качестве примера определим допустимые изменения тарифа занятой клетки (1, 3). Тариф клетки равен 5 усл. ед. за одно изделие. Уменьшение этой величины не повлияет на объем перевозок, так как указанное количество изделий в клетке удовлетворяет всю потребность магазина 3.
Если тариф клетки (3,1) становится больше 5 усл. ед., то при составлении циклов будет задействована пустая клетка (2, 3) с |Δ23| = 13 или (3, 3) с |Δ33| = 2. В обоих циклах клетка (1, 3) будет иметь знак "—" и любое увеличение тарифа повлечет снижение теневой цены пустой клетки (2, 3) или (3, 3).
Изменение объема перевозок будет иметь место в случае, если тариф клетки (1,3) возрастет более чем на 2 усл. ед. и превысит 7 усл. ед. При этом теневая цена клетки (3,3) станет положительной и окажется невыгодным использование клетки (1.3).
Таким образом, для получения оптимального распределения перевозок тариф клетки (1,3) должен изменяться в диапазоне от 0 до 7 усл. ед. Внутри указанного промежутка происходит лишь изменение общей стоимости транспортных расходов, а распределение перевозок не меняется.
Приложение транспортных моделей к решению некоторых экономических задач
Алгоритм и методы решения транспортной задачи могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов сij имеют различный смысл в зависимости от конкретной экономической задачи. К таким задачам относятся следующие:
— оптимальное закрепление за станками операций по обработке деталей. В них cij является таким экономическим показателем, как производительность. Задача позволяет определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. Так как транспортная задача требует нахождения минимума, то значения cij берутся с отрицательным знаком;
— оптимальные назначения, или проблема выбора. Имеется т механизмов, которые могут выполнять т различных работ с производительностью cij. Задача позволяет определить, какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности;
— задача о сокращении производства с учетом суммарных расходов на изготовление и транспортировку продукции;
— увеличение производительности автомобильного транспорта за счет минимизации порожнего пробега. Уменьшение порожнего пробега сократит количество автомобилей для перевозок, увеличив их производительность;
— решение задач с помощью метода запрещения перевозок. Используется в том случае, если груз от некоторого поставщика по каким-то причинам не может быть направлен одному из потребителей. Данное ограничение можно учесть, присвоив соответствующей клетке достаточно большое значение стоимости, тем самым в эту клетку не будут производиться перевозки.
23.12. Выбор оптимального варианта использования производственного оборудования
На предприятии имеются три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 130 ч.
Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.
Производительность каждой группы станков на каждую операцию задана матрицей
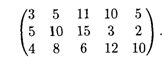
Решение. Воспользуемся алгоритмом решения закрытой транспортной задачи (табл. 23.13).
Так как в задаче требуется найти максимум, а согласно алгоритму транспортной задачи находится минимум, тарифы умножим на (—1).
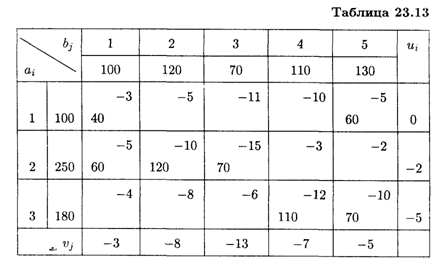
Находим потенциалы свободных клеток:
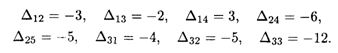
Так как Δ14 = 3 > 0, перераспределим грузы, получим
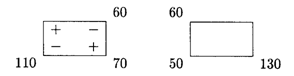
Полученное перераспределение грузов занесем в табл. 23.14.
Оценки свободных клеток составляют
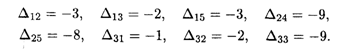
Найденное решение является оптимальным, так как все оценки свободных клеток отрицательные. Итак,
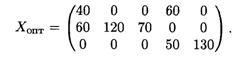
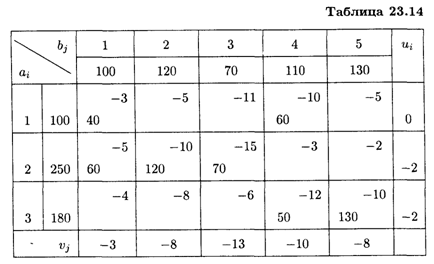
Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 ч соответственно, на второй группе — операции 1, 2 и 3 продолжительностью 60, 120 и 70 ч соответственно, на третьей группе — операции 4 и 5 продолжительностью 50 и 130 ч соответственно. При этом максимальное число обработанных деталей составит 5 170 шт.
УПРАЖНЕНИЯ
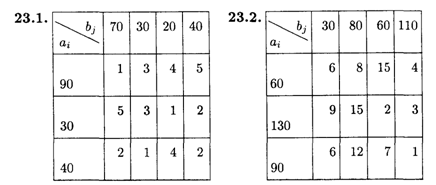
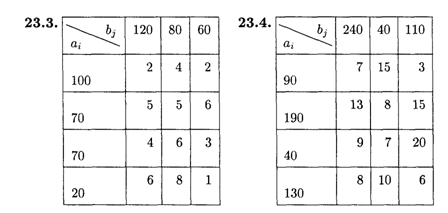
Решить следующие транспортные задачи, заданные распределительной таблицей.
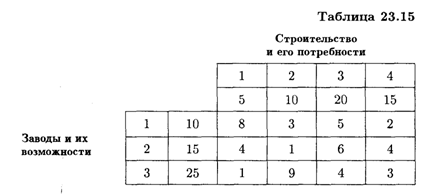
23.5. Требуется спланировать перевозку строительного материала с трех заводов к четырем строительным площадкам, используя железнодорожную сеть. В течение каждого квартала на четырех площадках требуется соответственно 5, 10, 20, 15 вагонов строительных материалов. Возможности различных заводов соответственно равны 10, 15 и 25 вагонов в квартал. Условия задачи даны в табл. 23.15. Числа на пересечении строк и столбцов таблицы означают стоимость перевозки одного вагона (усл. ед.).
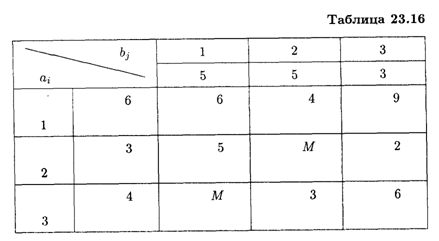
23.6. Решить транспортную задачу, заданную распределительной табл. 23.16, причем перевозки от 2-го поставщика ко 2-му потребителю и от 3-го поставщика к 1-му потребителю временно закрыты (в таблице эти тарифы обозначены большим числом М > 0).
23.7. В трех пунктах производства имеется одинаковая продукция в объеме 200, 170, 130 т. Эта продукция должна быть доставлена потребителям в количестве 50, 220, 80, 110 и 140 т. Стоимости перевозок единицы продукции от каждого поставщика к каждому потребителю заданы матрицей
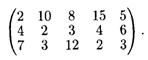
В связи с неплатежеспособностью перевозки от первого пункта производства до первого пункта потребления и от второго пункта производства до третьего пункта потребления временно закрыты. Составить оптимальный план перевозок, при котором суммарные затраты на них минимальные.
23.8. Фирма получила заказы на три вида выпускаемой ею продукции (бокалы, чашки и вазы), которые необходимо изготовить в течение следующей недели. Размеры заказов: бокалы — 4000 шт., чашки — 2400 шт., вазы — 1000 шт.
Участок по изготовлению имеет три станка, на каждом из которых можно делать любой из заказанных видов продукции с одинаковой производительностью. Однако единичные затраты по каждому виду продукции различны в зависимости от используемого станка и заданы табл. 23.17.
Кроме того, известно, что производственные мощности 2-го и 3-го станков на следующую неделю составят 3000 шт., а 1-го станка — 2000 шт.

Используя модель транспортной задачи, найти план производства для заказанных видов продукции, имеющий наименьшую стоимость.
