Экономический анализ задач с использованием теории двойственности
Рассмотрим задачу оптимального использования ресурсов, запишем ее математическую модель
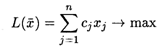
при ограничениях:
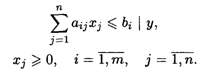
Двойственная задача имеет вид
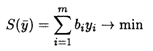
при ограничениях:
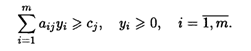
ТЕОРЕМА 3. Значения переменных уi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов системы ограничений исходной задачи на оптимальное значение ее целевой функции, т.е.
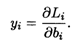
Примем 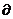 Li ≈ ΔLi,
Li ≈ ΔLi, 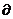 bi ≈ Δbi, тогда ΔLi ≈ yi • Δbi.
bi ≈ Δbi, тогда ΔLi ≈ yi • Δbi.
Для задачи оптимального использования сырья это уравнение показывает, что при изменении i-го ресурса оптимальный доход является линейной функцией от его приращения, причем коэффициентом служит уi — i-я компонента оптимального решения двойственной задачи.
Если yi мало, то значительному увеличению i-го ресурса будет соответствовать небольшое увеличение оптимального дохода и ценность ресурса невелика.
Если yi = 0, то при увеличении i-го ресурса оптимальный доход остается неизменным и ценность этого ресурса равна нулю. В самом деле, сырье, запасы которого превышают потребности в нем, не представляет ценности для производства и его оценку можно принять за нуль.
Если уi велико, то незначительному увеличению i-го ресурса будет соответствовать существенное увеличение оптимального дохода и ценность ресурса высока. Уменьшение ресурса ведет к существенному сокращению выпуска продукции.
Переменную уi считают некоторой характеристикой ценности i-го ресурса. В частности, при увеличении i-го ресурса на единицу (Δbi = 1) оптимальный доход возрастает на yi, что позволяет рассматривать yi как "условную цену", оценку единицы i-го ресурса, объективно обусловленную оценку.
Так как уi представляет частную производную от оптимального дохода по i-му ресурсу, то уi характеризует скорость изменения оптимального дохода при изменении i-го ресурса.
С помощью yi можно определить степень влияния ограничений на значение целевой функции. Предельные значения (нижняя и верхняя границы) ограничений ресурсов, для которых yi остаются неизменными, определяются по формулам:
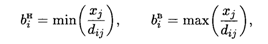
где xj — значение переменной в оптимальном решении; dij — элементы матрицы (dij) = А-1, обратной к матрице базиса оптимального решения, для которой А = (aij)mxn.
Если в план включаются новые виды продукции, то их оценка находится по формуле
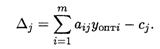
Если Δj < 0, то новый вид продукции улучшает план. При Δj > 0 нецелесообразно включать новый вид продукции.
22.5. Стратегическое планирование выпуска изделий с учетом имеющихся ресурсов
Фирма выпускает три вида изделий, располагая при этом сырьем 4 типов: А, Б, В, Г соответственно в количествах 18, 16, 8 и 6 т. Нормы затрат каждого типа сырья на единицу изделия первого вида составляют соответственно 1, 2, 1, 0, второго вида — 2, 1, 1, 1 и третьего вида — 1, 1, 0, 1. Прибыль от реализации единицы изделия первого вида равна 3 усл. ед., второго — 4 усл. ед., третьего — 2 усл. ед.
Требуется:
1) составить план производства трех видов, максимизирующих прибыль;
2) определить дефицитность сырья;
3) установить размеры максимальной прибыли при изменении сырья А на 6 т, Б — на 3 т, В — на 2 т, Г — на 2 т. Оценить раздельное влияние этих изменений и суммарное их влияние на прибыль;
4) оценить целесообразность введения в план производства фирмы нового вида изделий (четвертого), нормы затрат на единицу которого соответственно равны 1, 2, 2, 0, а прибыль составляет 15 усл. ед.
Решение. 1. Обозначим через 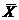 = (x1, x2, x3) план производства изделий трех видов, тогда математическая модель задачи примет вид
= (x1, x2, x3) план производства изделий трех видов, тогда математическая модель задачи примет вид
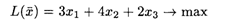
при ограничениях:
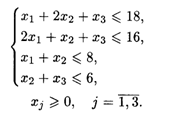
Решаем задачу симплексным методом, при этом последняя таблица будет иметь вид табл. 22.3.
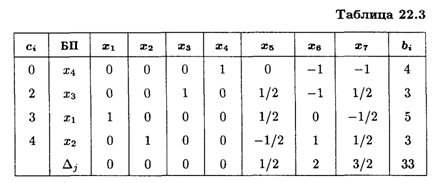
Из таблицы следует
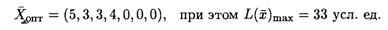
Согласно теоремам двойственности
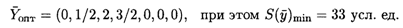
2. Наиболее дефицитным является сырье типа В, для которого двойственная оценка у3 = 2. Менее дефицитным является сырье вида Б, для которого у2 = 1/2. Совсем не дефицитным является сырье A (y1 = 0).
Для определения интервала устойчивости оценок найдем обратную матрицу для матрицы коэффициентов при базисных переменных в оптимальном решении системы ограничений. Базисными переменными в оптимальном решении являются x1, x2, х3, x4. Матрица коэффициентов при этих переменных в системе ограничений имеет вид
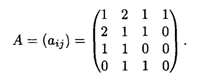
Тогда обратная матрица для матрицы А следующая:
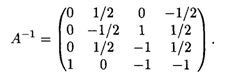
Найдем интервал устойчивости оценок по видам сырья:
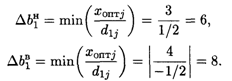
Интервал устойчивости оценок по отношению к первому ограничению:
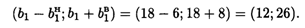
Аналогично определим интервалы устойчивости оценок по отношению к ограничениям остальных видов сырья:
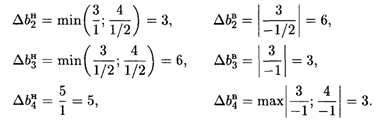
Интервалы устойчивости оценок по отношению ко второму ограничению:
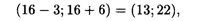
к третьему ограничению:
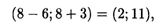
к четвертому ограничению:
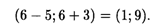
3. Изменения сырья согласно условиям задачи на +6, -3, +2, +2 т приводят к ограничению запаса сырья до 24, 13, 10, 8 т соответственно. Поскольку эти изменения находятся в пределах устойчивости оценок, на что указывают интервалы, то раздельное их влияние на прибыль определяется по формуле
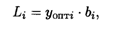
тогда
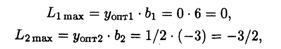
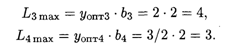
Суммарное влияние на прибыль:
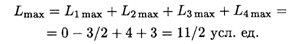
Если изменение сырья не находится в пределах устойчивости оценок, то необходимо найти новые условные оценки, т.е. решить задачу симплексным методом с изменением количества сырья соответствующих видов.
4. Для оценки целесообразности введения в план производства фирмы четвертого вида изделий используем формулу
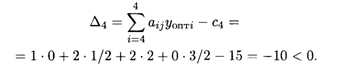
Так как прибыль превышает затраты, то введение в план производства четвертого вида изделий целесообразно.
УПРАЖНЕНИЯ
Для следующих задач составить математические модели двойственных задач и по решению исходной найти оптимальное решение двойственной.
22.1. L(  ) = x1 + 3x3 + 3x4 → min при ограничениях:
) = x1 + 3x3 + 3x4 → min при ограничениях:
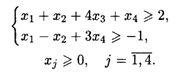
22.2. L(  ) = 2х1 + х2 – 3x3 + х4 → max при ограничениях:
) = 2х1 + х2 – 3x3 + х4 → max при ограничениях:
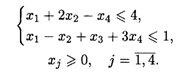
22.3. L(  ) = -х1 + x2 + 6x3 — х4 → min при ограничениях:
) = -х1 + x2 + 6x3 — х4 → min при ограничениях:
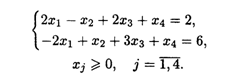
22.4. L(  ) = -3x2 + х3 – х4 → max при ограничениях:
) = -3x2 + х3 – х4 → max при ограничениях:
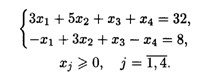
22.5. L(  ) = -3x1 + x2+ 3x3 – 4x4 → min при ограничениях:
) = -3x1 + x2+ 3x3 – 4x4 → min при ограничениях:
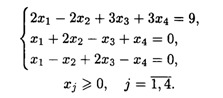
Составить математическую модель двойственных задач и по ее решению найти оптимальное решение исходной.
22.6. L(  ) = l,5x1 + 2х2 → max при ограничениях:
) = l,5x1 + 2х2 → max при ограничениях:
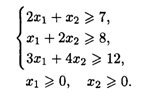
22.7. L(  ) = x1 - 2x2 + x4 → minпри ограничениях:
) = x1 - 2x2 + x4 → minпри ограничениях:
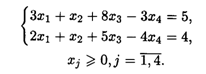
22.8. L(  ) = -2x1 + х2 → min при ограничениях:
) = -2x1 + х2 → min при ограничениях:
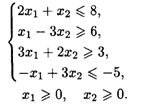
22.9. Для производства трех изделий А, В и С используются три вида сырья. Каждый из них используется в объеме, не превышающем 180, 210 и 236 кг. Нормы затрат каждого из видов сырья на одно изделие и цена единицы изделий приведены в табл. 22.4.

Определить план выпуска изделий, обеспечивающий получение максимального дохода.
Составить для данной задачи двойственную и найти:
1) оптимальный план двойственной задачи;
2) интервалы устойчивости двойственных оценок;
3) увеличение максимального дохода при увеличении количества сырья 2-го и 3-го видов на 80 и 160 кг соответственно и при уменьшении количества сырья 1-го вида на 40 кг. Оценить раздельное и суммарное влияние этих изменений;
4) целесообразность введения в план производства 4-го изделия, нормы затрат сырья на одно изделие которого составляют 2, 4 и 6 кг, а цена изделия равна 18 усл. ед.;
5) оптимальные планы исходной и двойственной задач, если количество сырья 1, 2 и 3 равно 140, 250 и 240 кг соответственно.
