Глава 22. двойственность в линейном программировании

Произвольную задачу линейного программирования можно определенным образом сопоставить с другой задачей линей­ного программирования, называемой двойственной. Первона­чальная задача является исходной. Эти две задачи тесно свя­заны между собой и образуют единую двойственную пару.

Различают симметричные, несимметричные и смешанные двойственные задачи.

Виды двойственных задач и составление их математических моделей

Симметричные двойственные задачи

Дана исходная задача

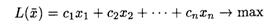
при ограничениях:

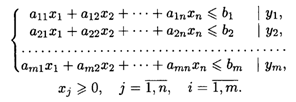
Задача дана в неканоническом виде. Составим математичес­кую модель двойственной задачи, для этого:

— каждому неравенству системы ограничений исходной за­дачи приводим в соответствие переменную y_i;

— составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений исход­ной задачи;

— составляем систему ограничений. Коэффициенты систе­мы ограничений образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи. Знаки неравенств меняются на противоположные;

— свободными членами системы ограничений являются ко­эффициенты целевой функции исходной задачи. Все пе­ременные двойственной задачи неотрицательные.

Математическая модель двойственной задачи имеет вид

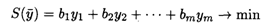
при ограничениях:

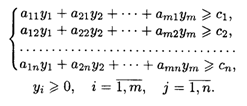
Несимметричные двойственные задачи

Дана исходная задача

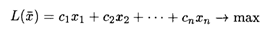
при ограничениях:

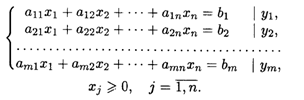
Задача дана в каноническом виде. Составим математичес­кую модель двойственной задачи.

Для ее составления пользуются тем же правилом, что и для составления симметричной задачи, с учетом следующих особенностей:

— ограничениями двойственной задачи будут неравенства. Если в целевой функции двойственной задачи требуется найти минимум, то знак неравенства ≥, если максимум, то ≤;

— переменные y_i — произвольные по знаку.

Математическая модель двойственной задачи имеет вид

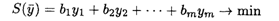
при ограничениях:

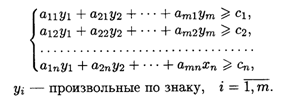
Смешанные двойственные задачи

Математическая модель исходной задачи имеет условия симметричных и несимметричных задач. При составлении двойственной задачи необходимо выполнять правила симмет­ричных и несимметричных задач.

Основные теоремы двойственности

ТЕОРЕМА 1. Если одна из двойственных задач имеет оп­тимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений и вы­полняется равенство

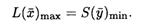
Если одна из двойственных задач неразрешима ввиду то­го, что L( )_max → (или S( 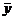)_min → - ), тo другая задача не имеет допустимых решений.

ТЕОРЕМА 2. Для оптимальности допустимых решени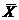й и 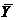пары двойственных задач необходимо и достаточно, что­бы они удовлетворяли системе уравнений

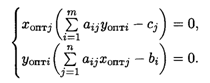
Теоремы позволяют определить оптимальное решение од­ной из пары задач по решению другой.

Решение двойственных задач

Решение симметричных задач

Рассмотрим решение задач с использованием теорем двой­ственности.

Решим исходную задачу графическим методом, получим 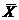_опт = (4, 1), при этом L( )_mах = 3.

На основании 1-й теоремы двойственности

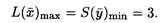
Так как x₁, х₂ > 0, то по 2-й теореме двойственности систе­му ограничений двойственной задачи можно записать в виде равенств:

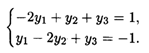
Подставим 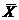_опт в систему ограничений исходной задачи:

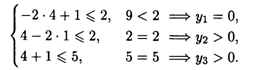
Тогда система ограничений двойственной задачи примет вид

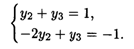
Откуда 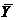_опт = (0, 2/3, 1/3), при этом S( 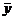)_min = 3.

Пусть дано решение двойственной задачи 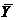_опт = (0, 2/3, 1/3), S( 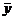)_min = 3, найдем решение исходной.

По 1-й теореме двойственности L( )_max = S( 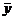)_min = 3. Так как у₂, y₃ > 0, то по 2-й теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства:

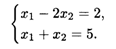
Откуда 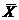_опт = (4,1), при этом L( )_mах = 3.

Рассмотрим решение задач методом, основанным на взаимно однозначном соответствии между переменными: основным переменным исходной задачи соответствуют балансовые переменные двойственной, и наоборот. Для этого решим двойственную задачу симплексным методом:

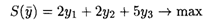
при ограничениях:

Из табл. 22.1 следует, что 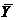_опт = (0, 2/3, 1/3), S( 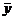)_min = 3.

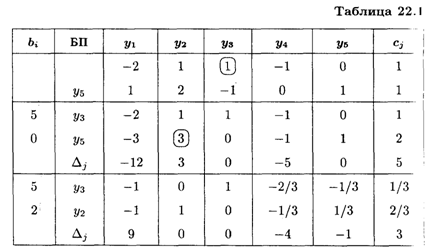
На основании 1-й теоремы двойственности получаем

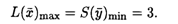
Решение другой задачи найдем по соответствию между пе­ременными:

Значение x_j определяем по последней симплексной таблице в строке Δ_i в соответствующем столбце, причем значения x_j ­берем по модулю:

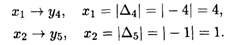
Таким образом, решение исходной задачи:

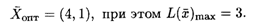
Если исходная задача решена симплексным методом, то ре­шение двойственной задачи может быть найдено по формуле

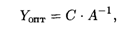
где С — матрица-строка коэффициентов при базисных пере­менных целевой функции в оптимальном решении исходной за­дачи; А^-1 — обратная матрица для матрицы А, являющейся матрицей коэффициентов базисных переменных системы огра­ничений исходной задачи в оптимальном решении.

Решим симплексным методом исходную задачу вида

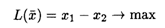
при ограничениях:

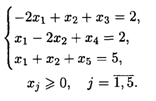
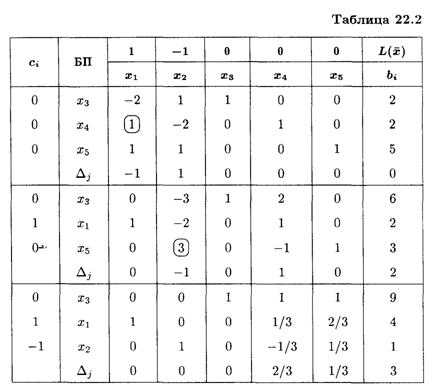
Из табл. 22.2 следует, что 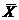_опт = (4,1), L( )_max = 3. Мат­рицы записываются в виде

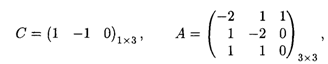
тогда

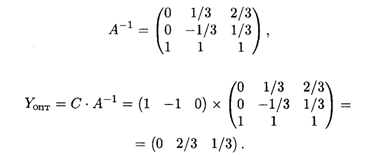
Таким образом, решение двойственной задачи следующее:

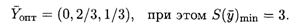
Решение несимметричных задач

Рассмотрим решение задач с использованием теорем двой­ственности.

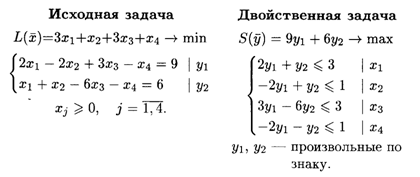
Решив двойственную задачу графическим методом, полу­чим

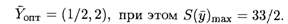
По 1-й теореме двойственности L( )_min = S( 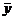)_max = 33/2.

Подставим 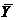_опт в систему ограничений двойственной за­дачи:

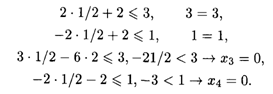
Так как х₃ = х₄ = 0, то система ограничений исходной задачи примет вид

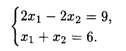
Решая данную систему, получим

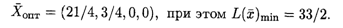
Рассмотрим решение задач с использованием обратной матрицы.

Пусть решение исходной задачи

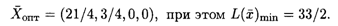
Решение двойственной задачи найдем по формуле

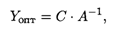
где

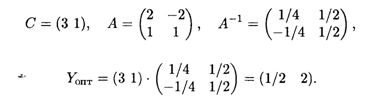
Таким образом, 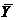_oпт = (1/2, 2), при этом S( 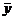)_max = 33/2.

Решение смешанных двойственных задач

Смешанные двойственные задачи можно решать с исполь­зованием теорем двойственности.

Найдем оптимальное решение двойственной задачи:

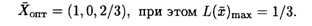
По 1-й теореме двойственности

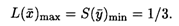
Так как х₁ > 0, x₃ > 0, то по 2-й теореме двойственности пер­вое и третье ограничения двойственной задачи выполняются в виде равенств: