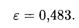Двумерная случайная величина

До сих пор мы рассматривали дискретные случайные ве­личины, которые называют одномерными: их возможные зна­чения определялись одним числом. Кроме одномерных вели­чин рассматривают также величины, возможные значения ко­торых определяются несколькими числами. Двумерную слу­чайную величину обозначают через (X, Y); каждая из величин X и Y называется компонентой (составляющей). Обе величи­ны Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Например, при штамповке стальных пластинок их длина и ширина представляют собой двумерную случайную величину.

Определение 1. Законом распределения двумерной случай­ной величины (X, Y) называют множество возможных пар чи­сел (x_i, y_j) и их вероятностей p(x_i, y_j). Двумерную случайную величину можно трактовать как случайную точку А(Х, Y) на координатной плоскости.

Закон распределения двумерной случайной величины обыч­но задается в виде таблицы, в строках которой указаны воз­можные значения x_i случайной величины X, а в столбцах — возможные значения y_j случайной величины Y, на пересече­ниях строк и столбцов указаны соответствующие вероятности p_ij. Пусть случайная величина Х может принимать п значе­ний, а случайная величина Y - т значений. Тогда закон рас­пределения двумерной случайной величины (X, Y) имеет вид

Из этой таблицы можно найти законы распределения каждой из случайных компонент. Например, вероятность того, что слу­чайная величина Х примет значение х_k, равна, согласно тео­реме сложения вероятностей независимых событий,

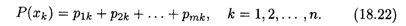
Иными словами, для нахождения вероятности Р(х_k) нужно просуммировать все т вероятностей по k-му столб­цу таблицы (18.21). Аналогично получается вероятность то­го, что случайная величина Y примет возможное значение у_r: Р(у_r) получается суммированием всех n вероятностей r-й стро­ки таблицы (18.21) (r = 1, 2, ... ,m). Отсюда следует, что сумма всех вероятностей в законе распределения (18.21) равна единице:

Пример 1. Задано распределение двумерной случайной вели­чины:

Найти распределения Х, Y и Х + Y.

Решение. В нашем случае возможные значения случайной величины X: х₁ = 1, х₂ = 2, x₃ = 3. Тогда, согласно формуле (18.22), имеем P(x₁) = 0,1 + 0,2 = 0,3, P(x₂) = 0,15 + 0,22 = 0,37, Р(x₃) = 0,12 + 0,21 = 0,33. Отсюда получаем закон распреде­ления X:

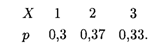
Аналогично получаем и для распределения Y: у₁ = 1, y₂ = 2; P(y₁) = 0,1 + 0,15 + 0,12 = 0,37, P(y₂) = 0,2 + 0,22 + 0,21 = 0,63;

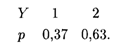
Теперь найдем распределение X+Y. Возможные значения этой случайной величины: 2, 3, 4 и 5. Соответствующие вероятнос­ти Р(2) = 0,1, Р(3) = 0,15 + 0,2 = 0,35, Р(4) = 0,12 + 0,22 = 0,34, Р(5) = 0,21. Отсюда находим искомое распределение:

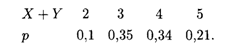
В случае системы двух случайных величин используются кроме математических ожиданий и дисперсий еще и другие числовые характеристики, описывающие их взаимосвязь.

Корреляционный момент

Определение 2. Корреляционным моментом случайных ве­личин Х и Y (или ковариацией) называется математическое ожидание произведений их отклонений:

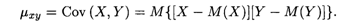
Корреляционный момент служит для описания связи между случайными величинами Х и Y. Из свойств математического ожидания легко убедиться в том, что μ_xy можно записать в следующем виде:

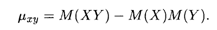
Для непосредственного вычисления корреляционного момен­та (ковариации) используется формула (см. распределение (18.21))

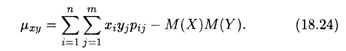
ТЕОРЕМА 3. Корреляционный момент двух независимых слу­чайных величин Х и Y равен нулю.

Если корреляционный момент μ_xу не равен нулю, то, стало быть, величины Х и Y являются зависимыми.

Коэффициент корреляции

Из определения корреляционного момента следует, что его размерность равна произведению размерностей величин Х и Y; например, если Х и Y измерены в сантиметрах, то μ_xy имеет размерность см².

Это обстоятельство затрудняет сравнение корреляционных моментов различных систем случайных величин. Для устране­ния этого недостатка вводят безразмерную числовую характе­ристику — коэффициент корреляции, величина которого не зависит от выбора системы измерения случайных величин.

Определение 3. Коэффициентом корреляции случайных ве­личин Х и Y называется отношение их корреляционного мо­мента к произведению средних квадратических отклонений этих величин:

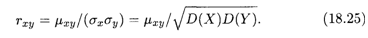
Из определения и свойств математического ожидания и дис­персии следует важный вывод, что абсолютная величина коэф­фициента корреляции не превосходит единицы:

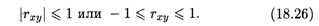
Определение 4. Две случайные величины Х и Y называются коррелированными, если их корреляционный момент (коэффи­циент корреляции) отличен от нуля; если же их корреляцион­ный момент равен нулю, то Х и Y называются некоррелированными.

Таким образом, две коррелированные случайные величины (т.е. при r_xy ≠ 0) являются также и зависимыми. Обратное утверждение неверно, т.е. две зависимые величины могут быть как коррелированными, так и некоррелированными.

Пример 2. Найти корреляционный момент и коэффициент корреляции двух случайных величин Х и Y, распределения которых заданы в предыдущем примере 1.

Решение. Воспользуемся формулами (18.24), (18.26), а также формулой вычисления центрального момента второго порядка (18.19); последовательно вычисляем: М(Х) = 2,03, М(Y) = 1,63, D(X) = 0,629, D(Y) = 0,233,

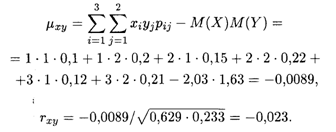
В данном случае коэффициент корреляции близок к нулю; это означает, что случайные величины Х и Y слабокоррелированы.

Линейная регрессия

Пусть (X, Y) — двумерная случайная величина, где Х и Y — зависимые случайные величины. Оказывается возмож­ным приближенное представление величины Y в виде линей­ной функции величины X:

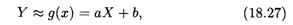
где а и b — параметры, подлежащие определению. Обычно эти величины определяются с помощью метода наименьших квад­ратов (см. п. 8.5).

Определение 5. Функция (18.27) называется наилучшим при­ближением в смысле метода наименьших квадратов, если ма­тематическое ожидание M[Y — g(Х)]² принимает наименьшее возможное значение. Функцию g(х) называют среднеквадратической регрессией Y на X.

ТЕОРЕМА 4. Линейная средняя квадратическая регрессия Y на Х имеет вид

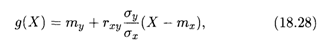
где r_xy определяется формулой (18.25), т_у = M(Y) и m_x = М(Х) — математические ожидания соответственно случайных величин Y и X.

Коэффициент b = r_xуσ_у / σ_x называют коэффициентом ре­грессии Y на Х, а прямую

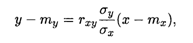
реализующую линейную зависимость (18.28) случайной вели­чины Y от случайной величины X, называют прямой среднеквадратической регрессии Х на Y. Поскольку зависимость (18.28) является приближенной, то существует погрешность этого приближения, называемая остаточной дисперсией:

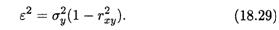
Аналогичную форму записи имеет прямая среднеквадратическая регрессия Х на Y:

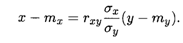
Пример 3. Найти линейную среднюю квадратическую регрес­сию и остаточную дисперсию случайной величины Y на слу­чайную величину Х по данным примеров 1 и 2.

Решение. Для двумерной случайной величины (X, Y), приведенной в примере 1, все необходимые числовые характе­ристики указаны в решении примера 2: m_x = 2,03, т_у = 1,63, r_ху = -0,023, σ_x = 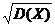= 0,793, σ_y = 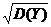= 0,483. Из уравнения (18.28) получаем искомое соотношение:

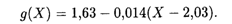
Остаточная дисперсия рассчитывается по формуле (18.29):

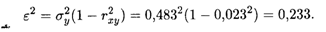
Для оценки среднеквадратичной погрешности линейной ре­грессии обычно используют величину ε, в нашем случае она составляет