Множества. Основные обозначения. Операции над множествами

Понятие множества является одним из основных в ма­тематике. Система, семейство, совокупность — эти термины можно считать синонимами слова "множество". Множество можно определить как совокупность объектов, объединенных по определенному признаку. Например, множество зрителей в данном кинотеатре; множество студентов определенного учеб­ного заведения; совокупность студентов, учащихся на "хоро­шо" и "отлично" в некоторой школе, совокупность коммерчес­ких банков, имеющих уставный фонд не ниже 100 миллиардов рублей. Множество может содержать конечное или бесконеч­ное число объектов.

Объекты, составляющие множество, называются его эле­ментами или точками. Обычно множества обозначаются боль­шими буквами, а входящие в них элементы — малыми буква­ми. Выражение "элемент х из множества Х" соответствует записи х 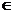Х (х принадлежит X); если же элемент х не вхо­дит в множество X, то это соответствует записи х 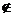Х (х не принадлежит X).

Пусть Х и Y — два множества. Тогда между ними мож­но определить следующие соотношения. Если оба множества состоят из одних и тех же элементов, то они совпадают, что соответствует записи X=Y. Если все элементы множества Х содержатся в множестве Y, то Х целиком содержится в Y, или Х 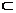Y (X является подмножеством множества Y). Если ни один элемент множества Х не содержится в Y, то, значит, и само множество X не содержится в Y, или X 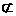Y.

В математике используется понятие пустого множества, обозначаемого символом Ø. Это множество, в котором не содер­жится ни один элемент, и потому оно является подмножеством любого множества.

Введем также понятия суммы множеств и их пересечения. Суммой или объединением двух множеств Х и.Y называет­ся совокупность элементов, входящих как в множество X, так и в множество Y. Сумма этих множеств обозначается X 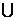Y. Например, пусть Х — множество государственных предприя­тий с годовым оборотом не ниже S денежных единиц, а Y — множество негосударственных предприятий с тем же порогом годового оборота; тогда Х 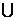Y будет множеством всех пред­приятий с указанным нижним ограничением S.

Отметим, что добавление пустого множества Ø к любому множеству Х не меняет этого множества, т.е.

Х 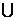Ø = Х.

Пересечением множеств Х и Y (или их общей частью) яв­ляется совокупность элементов, входящих как в множество X, так и в множество Y; это множество обозначается Х 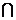Y. На­пример, если Х — это множество предприятий с годовым обо­ротом Т не ниже s, а Y — совокупность предприятий с годовым оборотом не более S, причем s < S, то в пересечение Х 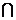Y войдут объекты с годовым оборотом T, удовлетворяющим не­равенству

s ≤ T ≤ S.

Отсутствие элементов со свойствами множеств Х и У одновременно означает, что пересечение этих множеств представ­ляет собой пустое множество Ø. Схематически пересечение двух множеств показано на рис. 1.1 (заштрихованная область).

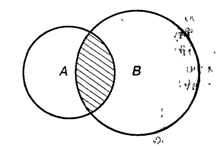
Рис. 1.1

Разностью множеств Х и Y называется множество Z, со­держащее все элементы множества X, не содержащиеся в Y; эта разность обозначается Z = Х \ Y.

В общем случае сложение и пересечение определяются для любого конечного числа множеств путем последовательного попарного проведения соответствующих операций.

В математических формулировках довольно часто исполь­зуются отдельные предложения и слова, так что при их записи целесообразно употреблять экономную логическую символику. Вместо выражения "любое х из множества X" употребима за­пись 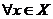, где перевернутая латинская буква 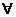взята от начала английского словаAny — любой. Аналогично вместо выражения "существует элемент х из множества X" кратко пишут: 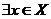, где перевернутая латинская буква 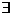является начальной в английском словеExistence — существование.