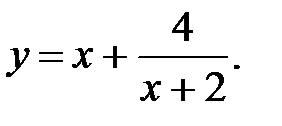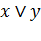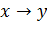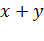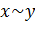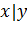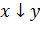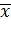Указания к решению задач контрольной работы №2
К задаче 2.1
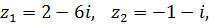
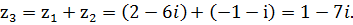
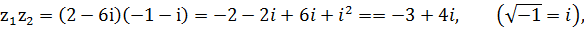
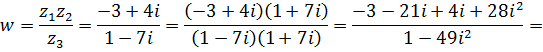
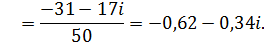
Проверка: 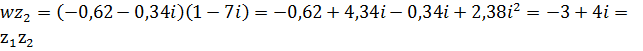 .
.
К задаче 2.2
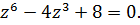
Обозначим 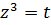 , тогда данное уравнение преобразуется в квадратное уравнение относительно
, тогда данное уравнение преобразуется в квадратное уравнение относительно 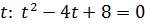 . Его корни
. Его корни 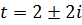 , следовательно, корнями z исходного уравнения являются числа
, следовательно, корнями z исходного уравнения являются числа 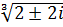 .
.
Числа 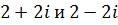 сопряженные, поэтому модули у них одинаковые, равные
сопряженные, поэтому модули у них одинаковые, равные 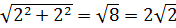 , а аргументы отличаются знаком:
, а аргументы отличаются знаком:
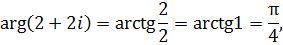
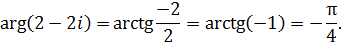
Используя формулу
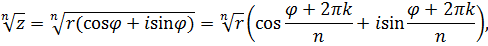
где 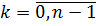 , находим корни:
, находим корни:
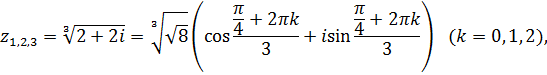
или
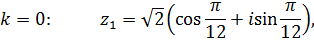
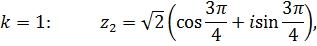
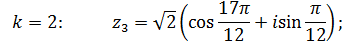
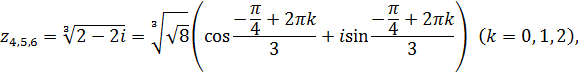
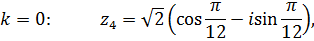
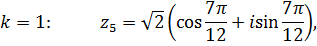
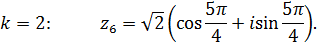
К задачам 2.3
а) Сколькими способами могут распределиться 15 перенумерованных бильярдных шаров в 6 различных лузах?
Число распределений перенумерованных шаров в 6 лузах равно числу размещений с повторениями из 6 элементов по 15, то есть 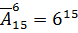 – каждый шар может попасть в любую из 6 луз и такой выбор надо сделать 15 раз.
– каждый шар может попасть в любую из 6 луз и такой выбор надо сделать 15 раз.
Формула числа способов размещения n различных предметов по m различным ящикам

б) Сколькими способами могут распределиться 15 одинаковых шаров в 6 различных лузах?
В этой задаче размещаемые шары одинаковы, поэтому число распределений одинаковых шаров в 6 лузах равно числу сочетаний с повторениями из 6 элементов по 15
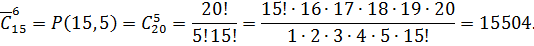
Формула числа способов размещения n одинаковых предметов по m различным ящикам
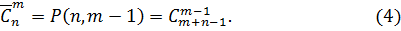
в) Сколькими способами могут распределиться 15 шаров, из которых 5 белых, 8 черных и 2 красных в двух различных лузах; в шести различных лузах?
Видим, что белые шары могут разместиться в 2 лузах 6 способами – в первую лузу может не попасть ни одного белого шара, 1, 2, 3, 4, все 5 шаров. Точно так же черные шары могут распределиться 9 способами, а красные – 3 способами. Так как шары каждого цвета попадают в лузы независимо от шаров другого цвета, то по правилу произведения получаем 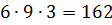 способов распределения шаров.
способов распределения шаров.
Формула числа распределения 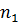 предметов одного вида,
предметов одного вида, 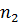 предметов другого вида, …,
предметов другого вида, …, 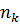 предметов k-го вида (предметы одного и того же вида неотличимы друг от друга) по двум различным ящикам
предметов k-го вида (предметы одного и того же вида неотличимы друг от друга) по двум различным ящикам
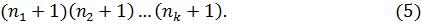
Число способов распределения этих же шаров в 6 лузах (число луз больше двух) равно
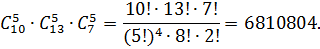
Формула числа распределения 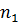 предметов одного вида,
предметов одного вида, 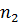 предметов другого вида, …,
предметов другого вида, …, 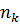 предметов k-го вида (предметы одного и того же вида неотличимы друг от друга) по m различным ящикам
предметов k-го вида (предметы одного и того же вида неотличимы друг от друга) по m различным ящикам
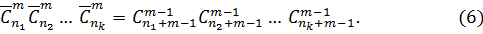
г) Сколькими способами могут распределиться 15 перенумерованных шаров по 3 лузам, чтобы в первой и второй лузах оказалось по 6 шаров, а в третьей 3 шара?
Разложим все шары в ряд по порядку и надпишем над каждым шаром номер лузы, в которую его кладут. Получившаяся последовательность номеров луз образует перестановку с повторениями, состоящую из шести чисел 1, шести чисел 2 и трех чисел 3. Каждая раскладка шаров по лузам определяет такую перестановку. И, наоборот, каждая такая перестановка определяет свой способ раскладки – в первую лузу попадают те шары, над которыми стоит 1, во вторую – над которыми стоит 2 и в третью – над которыми стоит 3. Тем самым устанавливается соответствие между перестановками с повторениями и раскладкой шаров по лузам. Поэтому число различных раскладок по лузам равно числу соответствующих перестановок с повторениями
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>в?™3!</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>=210210.</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 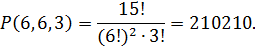
Формула числа способов распределения 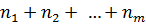 разных предметов по m различным ящикам так, чтобы в первый ящик попало
разных предметов по m различным ящикам так, чтобы в первый ящик попало 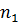 предметов, во второй –
предметов, во второй – 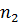 предметов, …, в m-й –
предметов, …, в m-й – 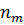 предметов
предметов
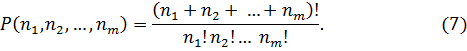
К задаче 2.4
Для функции 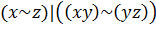 составить таблицу истинности, написать для неё совершенную ДНФ и совершенную КНФ.
составить таблицу истинности, написать для неё совершенную ДНФ и совершенную КНФ.
Используем основные функции дискретной математики для составления таблицы истинности:
Конъюнкция (функция и)
| Дизъюнкция (функция или)
| Импликация (следование)
| Сложение по модулю 2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эквивалентность (подобие)
| Штрих Шеффера (отрицание конъюнкции)
| Стрелка Пирса (отрицание дизъюнкции)
| Отрицание
|
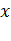 | 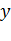 |  | 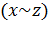 | 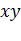 | 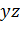 | 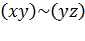 | 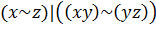 |
Составим совершенную ДНФ и совершенную КНФ по полученной таблице.
Совершенную ДНФ составляем по единицам таблицы истинности, причем, если 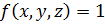 , то, если
, то, если 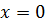 – в соответствующей конъюнкции совершенной ДНФ берем
– в соответствующей конъюнкции совершенной ДНФ берем 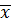 , а если
, а если 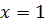 – в совершенной ДНФ берем
– в совершенной ДНФ берем 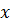 . Аналогично поступаем и с другими переменными, поэтому совершенная ДНФ для данной функции имеет вид:
. Аналогично поступаем и с другими переменными, поэтому совершенная ДНФ для данной функции имеет вид:
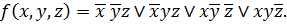
Совершенную КНФ составляем по нулям таблицы истинности, то есть, если 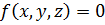 и
и 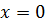 , то в соответствующей дизъюнкции берём
, то в соответствующей дизъюнкции берём 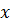 , а если
, а если 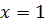 , то
, то 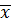 . Таким образом, совершенная КНФ для данной функции имеет вид:
. Таким образом, совершенная КНФ для данной функции имеет вид:
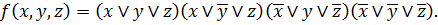
К задаче 2.5
Для орграфа найдем кратчайший путь от x к y с помощью алгоритма Дейкстры:
| y |
| v1 |
| v3 |
| x |
| v2 |
| v4 |
| v5 |
Работу алгоритма представим в виде таблицы, элементами на пересечении i-й строки и j-го столбца которой являются метки j-й вершины после i-го шага. Постоянные метки помечены знаком «*». В скобках около метки каждой вершины указано, из какой вершины она была помечена.
| Вершины Шаги алгоритма | x | v1 | v2 | v3 | v4 | v5 | y |
| 0* | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| 0* | 7(x) | 2*(x) | ∞ | ∞ | ∞ | ∞ | |
| 0* | 5*(v2) | 2*(x) | 10(v2) | 7(v2) | ∞ | ∞ | |
| 0* | 5*(v2) | 2*(x) | 10(v2) | 6*(v1) | ∞ | 15(v1) | |
| 0* | 5*(v2) | 2*(x) | 9*(v4) | 6*(v1) | 13(v4) | 15(v1) | |
| 0* | 5*(v2) | 2*(x) | 9*(v4) | 6*(v1) | 11*(v3) | 13(v3) | |
| 0* | 5*(v2) | 2*(x) | 9*(v4) | 6*(v1) | 11*(v3) | 12*(v5) |
Подробно опишем, как вычисляются метки вершин.
Шаг 0. В начальный момент вершина x имеет постоянную метку
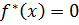 , а все остальные вершины орграфа – временные метки
, а все остальные вершины орграфа – временные метки 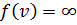 , что соответствует тому, что в орграфе могут быть вершины, недостижимые из x.
, что соответствует тому, что в орграфе могут быть вершины, недостижимые из x.
Шаг 1. Из вершины x выходят дуги в вершины 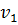 и
и 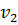 . Пересчитываем метки этих вершин и заполняем вторую строку таблицы:
. Пересчитываем метки этих вершин и заполняем вторую строку таблицы:
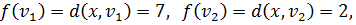
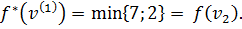
Метка вершины 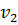 становится постоянной, равной 2.
становится постоянной, равной 2.
Шаг 2. Из вершины 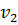 выходят дуги в еще неупорядоченные вершины
выходят дуги в еще неупорядоченные вершины 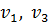 и
и 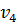 . Пересчитываем их временные метки:
. Пересчитываем их временные метки:
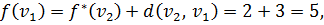
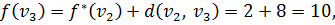
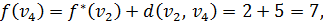
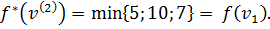
Метка из вершины 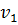 становится постоянной, равной 5.
становится постоянной, равной 5.
Шаг 3. Из вершины 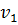 выходят дуги в еще неупорядоченные вершины
выходят дуги в еще неупорядоченные вершины 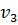 ,
, 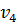 и y. Тогда
и y. Тогда
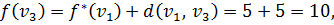
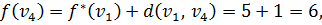
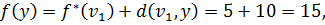
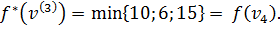
Метка вершины 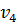 становится постоянной, равной 6.
становится постоянной, равной 6.
Шаг 4. Из вершины 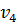 выходят дуги в еще неупорядоченные вершины
выходят дуги в еще неупорядоченные вершины 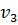 и
и 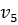 . Тогда
. Тогда
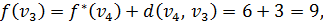
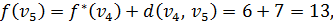
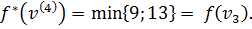
Метка вершины 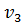 становится постоянной, равной 9.
становится постоянной, равной 9.
Шаг 5. Из вершины 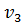 выходят дуги в неупорядоченные вершины
выходят дуги в неупорядоченные вершины 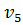 и y. Пересчитываем временные метки этих вершин и заполняем соответствующую строку таблицы:
и y. Пересчитываем временные метки этих вершин и заполняем соответствующую строку таблицы:
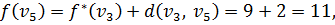
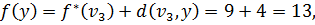
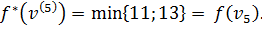
Метка вершины 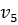 становится постоянной, равной 11.
становится постоянной, равной 11.
Шаг 6. Из вершины 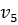 выходит дуга в неупорядоченную вершину y:
выходит дуга в неупорядоченную вершину y:
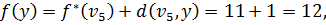
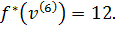
Заполняем последнюю строку таблицы. На этом шаге упорядочиваем последнюю неупорядоченную вершину y.
Итак, длина кратчайшего пути из x в y равна 12. Выписывая по порядку вершины, из которых помечалась вершина y и предшествующие ей вершины, получаем 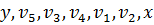 . Инвертируя данную последовательность, получаем кратчайший путь из x в y:
. Инвертируя данную последовательность, получаем кратчайший путь из x в y: 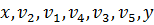 .
.
Контрольная работа №3
Задача 3.1.Вычислить пределы данных функций.
1. а) 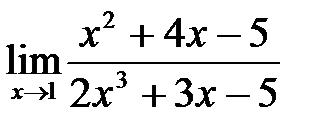 ; б)
; б) 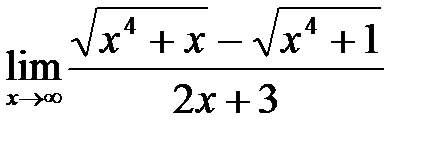 ;
;
в) 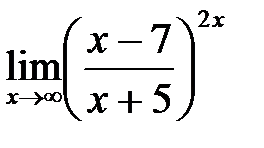 ; г)
; г) 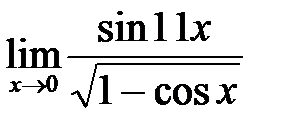 .
.
2. а) 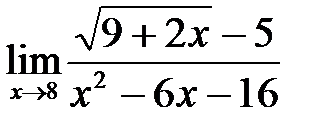 ; б)
; б) 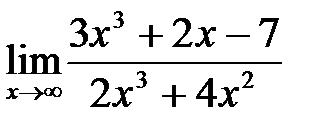 ;
;
в) 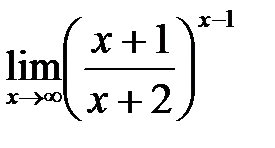 ; г)
; г) 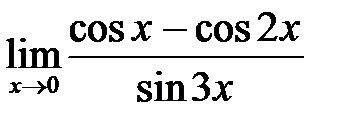 .
.
3. а) 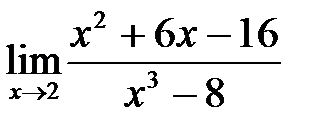 ; б)
; б) 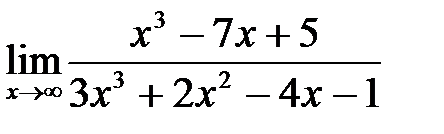 ;
;
в) 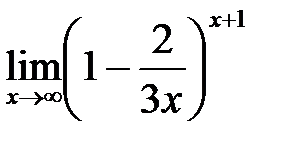 ; г)
; г) 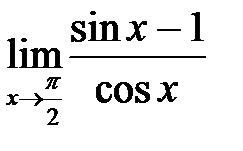
4. а) 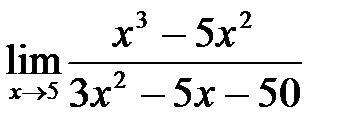 ; б)
; б) 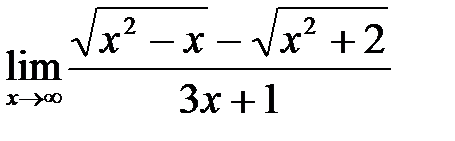 ;
;
в) 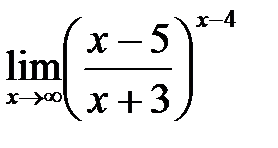 ; г)
; г) 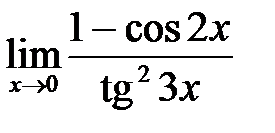 .
.
5. а) 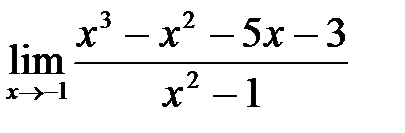 ; б)
; б) 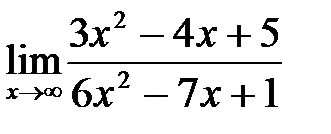 ;
;
в) 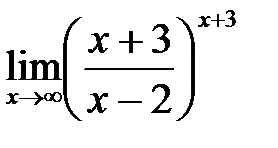 ; г)
; г) 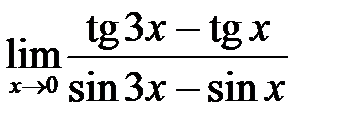 .
.
6. а) 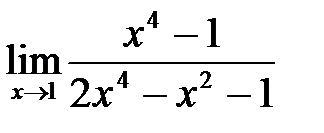 ; б)
; б) 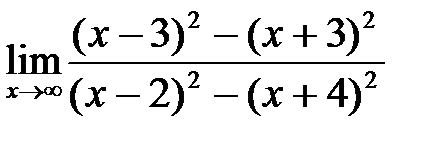 ;
;
в) 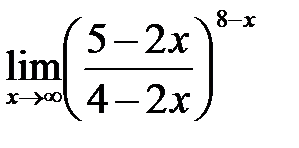 ; г)
; г) 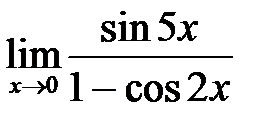 .
.
7. а) 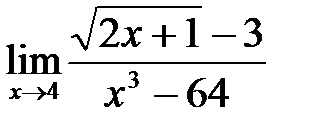 ; б)
; б) 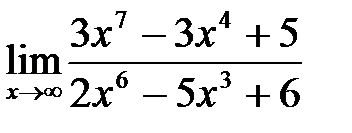 ;
;
в) 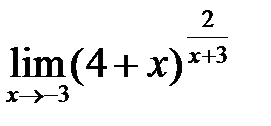 ; г)
; г) 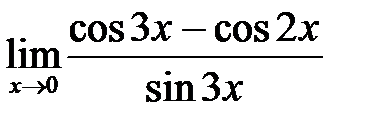 .
.
8. а) 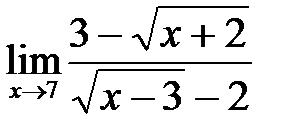 ; б)
; б) 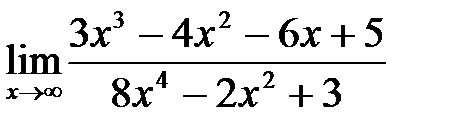 ;
;
в) 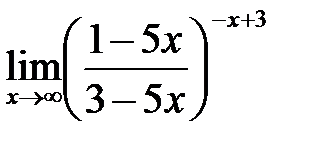 ; г)
; г) 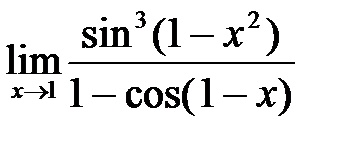 .
.
9. а) 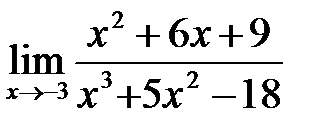 ; б)
; б) 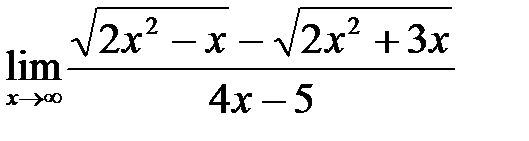 ;
;
в) 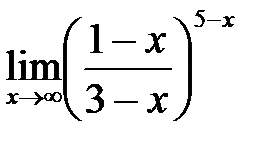 ; г)
; г) 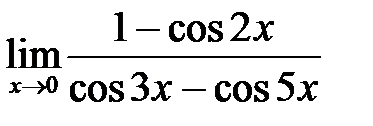 .
.
10. а) 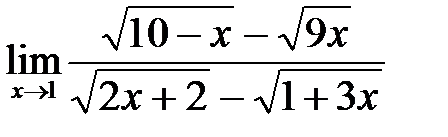 ; б)
; б) 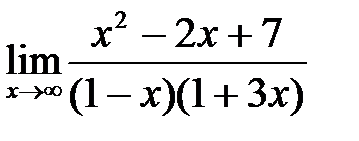 ;
;
в) 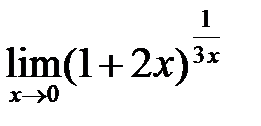 ; г)
; г) 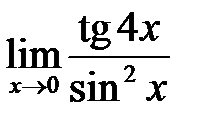 .
.
Задача 3.2.Определить то значение параметра А, для которого функция 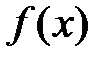 будет непрерывной. Сделать чертеж.
будет непрерывной. Сделать чертеж.
1. 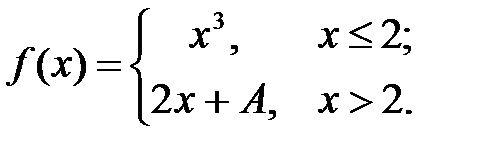 2.
2. 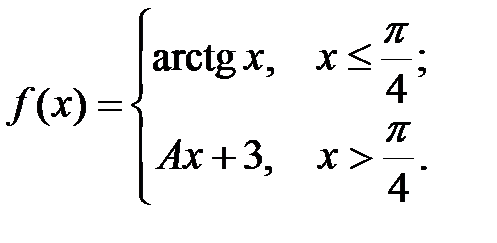
3. 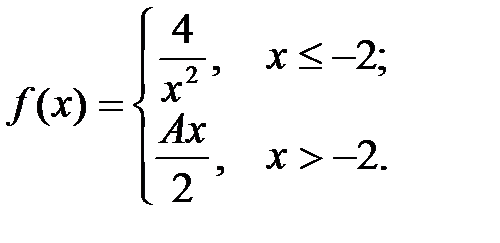 4.
4. 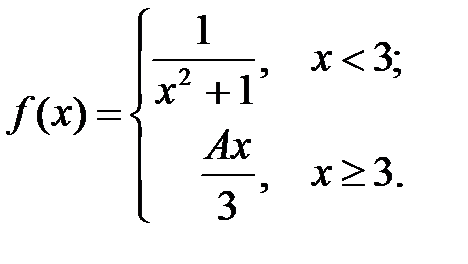
5. 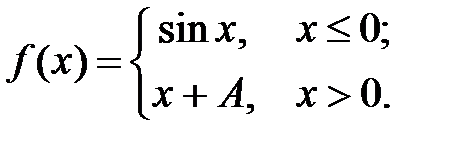 6.
6. 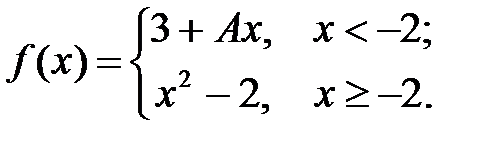
7. 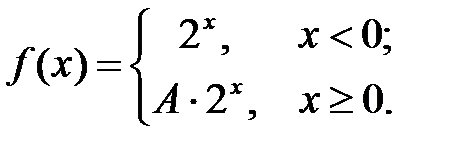 8.
8. 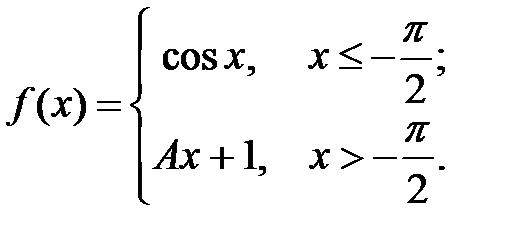
9. 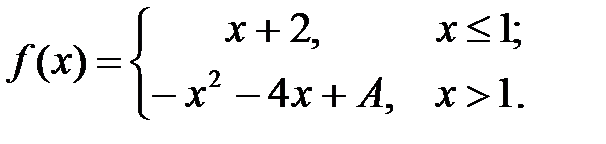 10.
10. 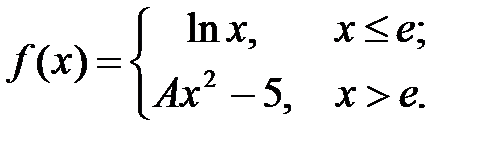
Задача 3.3.Найти производные функций.
1. а) 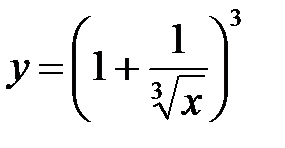 ; б)
; б) 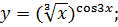
в) 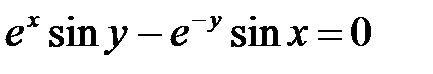 ; г)
; г) 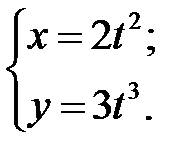
2. а) 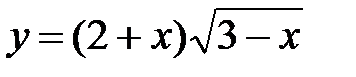 ; б)
; б) 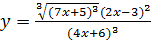 ;
;
в) 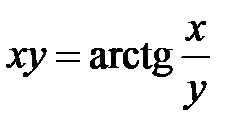 ; г)
; г) 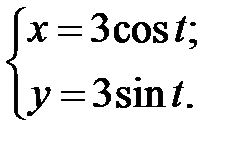
3. а) 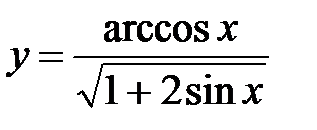 ; б)
; б) 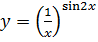 ;
;
в) 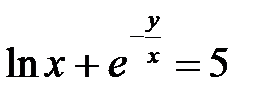 ; г)
; г) 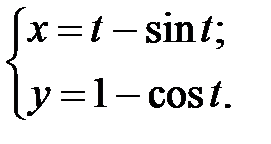
4. а) 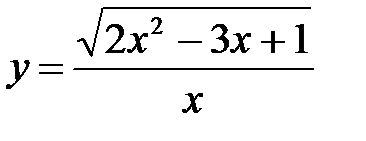 ; б)
; б) 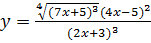 ;
;
в) 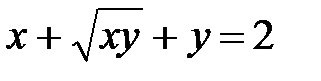 ; г)
; г) 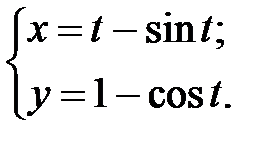
5. а) 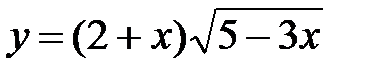 ; б)
; б) 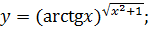
в) 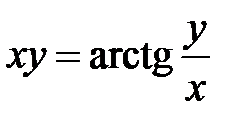 ; г)
; г) 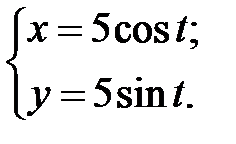
6. а) 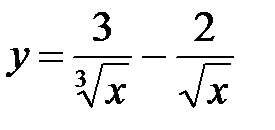 ; б)
; б) 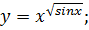
в) 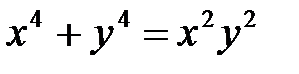 ; г)
; г) 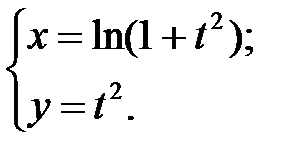
7. а) 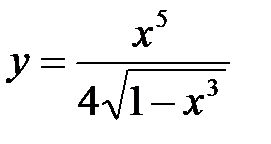 ; б)
; б) 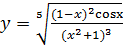 ;
;
в) 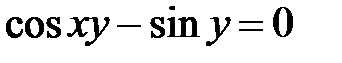 ; г)
; г) 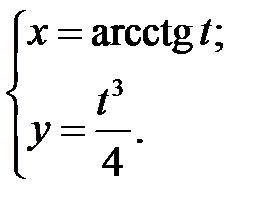
8. а) 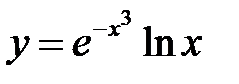 ; б)
; б) 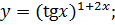
в) 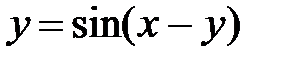 ; г)
; г) 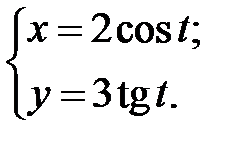
9. а) 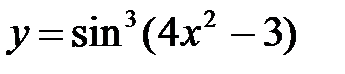 ; б)
; б) 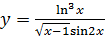 ;
;
в) 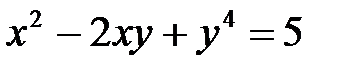 ; г)
; г) 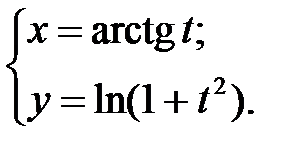
10. а) 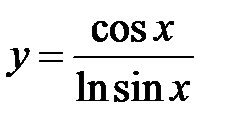 ; б)
; б) 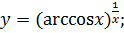
в) 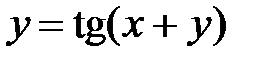 ; г)
; г) 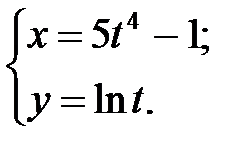
Задача 3.4.Найти пределы, используя правило Лопиталя.
1. 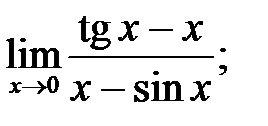 2.
2. 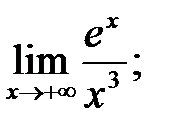
3. 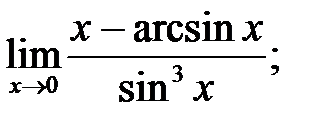 4.
4. 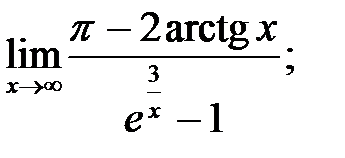
5. 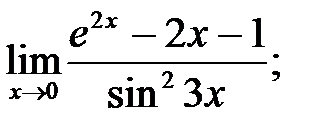 6.
6. 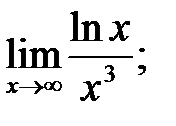
7. 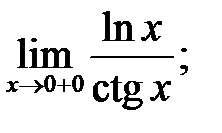 8.
8. 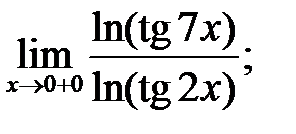
9. 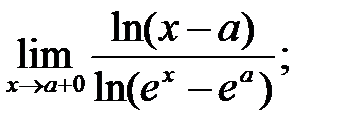 10.
10. 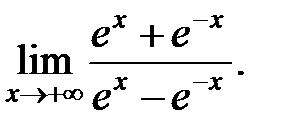
Задача 3.5.Исследовать функцию методами дифференциального исчисления и построить график.
1. 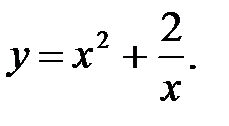 2.
2. 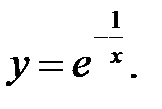
3. 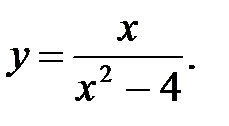 4.
4. 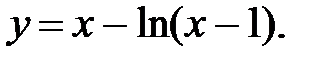
5. 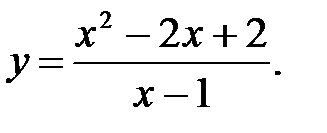 6.
6. 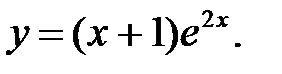
7. 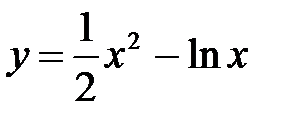 8.
8. 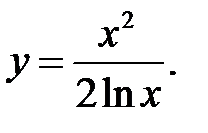
9. 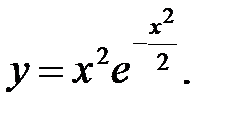 10.
10.