Вероятность случайных событий

Чтобы охарактеризовать вероятность события числом, нужно установить единицу измерения вероятности. Здесь поступают следующим образом: достоверному событию приписывают вероятность, равную единице; невозможному – равную нулю. Таким образом, вероятность P(A) события А должна удовлетворять следующим условиям:

1) P(A)=1, если А – достоверное событие;

2) P(A)=0, если А – невозможное событие;

3) 0<P(A)<1, если А – случайное событие.

Существует несколько подходов к нахождению вероятности события: классический, геометрический, статистический, аксиоматический. Мы рассмотрим только классическое и статистическое определения вероятности.

Классическое определение вероятности основано на понятии равновозможности (или равновероятности). Это понятие относится к числу первичных, не подлежащим формальному определению. Оно лишь поясняется рядом простых и доступных примеров. Например, выпадение одной из сторон монеты или одной из граней игральной кости – равновозможные события. Это утверждение опирается на повседневную практику и симметрию изучаемого объекта. Симметрия возможных исходов чаще всего наблюдается в искусственно организованных опытах, где приняты специальные меры для ее обеспечения (например, тасовка карт или костей домино, которая для того и производится, чтобы каждая из них могла быть выбрана с одинаковой вероятностью; или же приемы случайного выбора группы изделий для контроля качества в производственной практике). В таких опытах подсчет вероятностей производится проще всего. Не случайно первоначальное свое развитие теория вероятностей получила на материале азартных игр.

Говорят, что несколько событий образуют полную группу, если в результате опыта неизбежно должно появиться хотя бы одно из них. Примеры событий, образующих полную группу: 1) появление «1», «2», «3», «4», «5», «6» очков при бросании игральной кости; 2) «два попадания», «два промаха», «одно попадание» при двух выстрелах по мишени; 3) «появление хотя бы одного белого», «появление хотя бы одного черного» шара при вынимании двух шаров из урны. Несовместные события, образующие полную группу, называются элементарными событиями (или элементарными исходами). Отметим, что события первого и второго примеров являются элементарными, а третьего – нет, т.к. они совместны.

Элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. Например, при бросании одной игральной кости для события, состоящего в том, что выпадет не более двух очков, благоприятствующими элементарными исходами будут выпадение «1» или «2» очков.

Классическое определение вероятности: вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможныхнесовместных элементарных исходов, образующих полнуюгруппу:

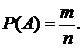(15.1)

При вычислении вероятностей по классической схеме приходится решать фактически комбинаторные задачи. При решении конкретной комбинаторной задачи нужно вначале выяснить, каким способом вы будете ее решать, либо непосредственным применением принципов умножения и сложения, либо применением комбинаторных формул, но перед этим нужно выяснить какой вид комбинации имеется в задаче, важен ли в ней порядок или нет, допускаются повторения или нет.

Пример 15.1. В колоде 36 карт. Какова вероятность вынуть: а) туза; б) туза пик; в) тузы красного цвета; г) любую карту, кроме туза.

Решение. Найдем общее число возможных исходов. Поскольку вынимается только одна карта, то число всевозможных исходов будет n=36. Найдем число благоприятствующих исходов для каждого случая. а) В колоде всего четыре туза, следовательно, m₁=4. Тогда

.

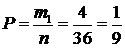б) Имеется всего один пиковый туз, т.е. m₂=1 и

.

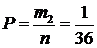в) Тузов красного цвета в колоде два (черви и бубни), т.е. m₃=2 и

.

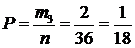г) Карт, отличающихся от туза, в колоде всего m₄=32. Следовательно, искомая вероятность будет равна

.

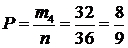Пример 15.2. На школьной вечеринке разыгрывается 100 билетов, из них 25 – выигрышных. Главный приз – компьютер – 1, игровых приставок – 5 и остальные призы поощрительные – шариковые ручки. Какова вероятность того, что владелец одного билета: а) выиграет главный приз; б) выиграет ценный приз; в) хоть что-нибудь выиграет; г) выбросит деньги на ветер?

Решение. Очевидно, что общее исходов n=100. Рассмотрим каждую из ситуаций отдельно. а) Благоприятствующих исходов выиграть компьютер только один: m₁=1. Поэтому вероятность выиграть компьютер будет

.

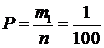б) Для второго случая 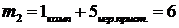, т.е. вероятность выиграть ценный приз

.

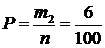в) Всего выигрышных билетов m₃=25, следовательно, вероятность хоть что-нибудь выиграть равна

.

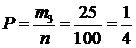8) Поскольку проигрышных билетов m₄=75, то вероятность выбросить деньги на ветер, т.е. ничего не выиграть, равна

.

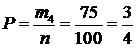Пример 15.3. В урне содержатся 3 синих, 5 красных и 2 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты либо два белых шара, либо два разных цветных (синий и красный) шара.

Решение. Поскольку в данной задаче неважен порядок, то для решения будем применять сочетания без повторения (шары не возвращаются обратно в урну). Найдем общее число возможных исходов:

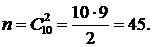
Теперь найдем число благоприятствующих возможных исходов. Два белых шара можно вынуть m₁=C₂²=1 способом, два разных цветных шара m₂=C₃¹×C₅¹=3×5=15 способами. Тогда общее число благоприятствующих исходов, в соответствии с принципом сложения, равно m = m₁+m₂ = 16. Таким образом,

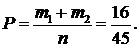
Пример 15.4. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность, что в нем все цифры разные?

Решение. Предположим, что равновозможны появления любой из 10 цифр во всех позициях телефонного номера. Поскольку при составлении пятизначным номеров важен порядок и возможны повторения, то общее число возможных пятизначных номеров будет равно

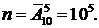
Номера, у которых все цифры разные, – это размещения без повторений

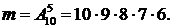
Таким образом, искомая вероятность (при сделанном предположении) будет равна

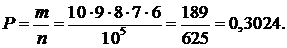
Упражнения

15.1. Зенитная батарея, состоящая из 3 орудий, производит залп по группе, состоящей из 4 самолётов. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят: а) по разным самолётам; б) по одному и тому же самолёту.

Решение: В данной задаче важен порядок, т.е. различается, какое орудие и по какому самолету выстрелило. Следовательно, в данной задаче мы имеем дело с размещениями. Поскольку орудия могут выстрелить по одному и тому же самолету, то общее число возможных исходов будет равно числу размещений с повторениями .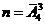

а) Если все орудия выстрелят по разным самолетам, то будем иметь дело с размещениями без повторений. Тогда число благоприятствующих исходов будет равно 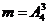. Таким образом, .

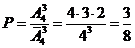б) Если все орудия выстрелят по одному и тому же самолету, то число благоприятствующих исходов будет равно 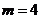. Таким образом, .

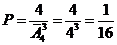15.2. Собрание, на котором присутствуют 20 человек, в том числе 8 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью?

Ответ: .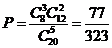

15.3. Для уменьшения общего количества игр 10 команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся в одной подгруппе.

Решение: В данной задаче порядок неважен, т.е. не принимается во внимание порядок отбора команд в группу. Следовательно, в данной задаче мы имеем дело с сочетаниями. Для того чтобы разбить 10 на две равные подгруппы достаточно выбрать 5 команд, которые и образуют одну из подгрупп, тогда остальные образуют другую подгруппу. Таким образом, общее число разбиений команд на две равные подгруппы будет равно 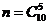. Для того, чтобы разбить команды на две подгруппы с указанными условиями, можно поступить следующим образом. Либо выбрать две наиболее сильные команды (это можно сделать способами 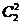), а затем добавить к ним 3 оставшиеся команды из оставшихся 8 не самых сильных команд ( 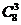способов). Либо выбрать сразу 5 команд из 8 не самых сильных команд ( 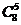способов). Тогда число благоприятствующих исходов будет равно 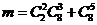. Таким образом, .

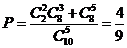15.4. Шесть различных книг случайных образом расставляют на полке. Найти вероятность того, что две определенные книги окажутся рядом.

Ответ: .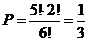

15.5. 10 вариантов контрольной работы распределены среди 6 студентов. Найти вероятность того, что варианты с номерами 1, 2 и 3 не будут использованы.

Ответ: .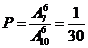

15.6. В первой урне находятся 5 белых и 3 черных шара, во второй – 4 белых и 6 черных шаров. Из каждой урны случайным образом вынули по одному шару. Найти вероятность того, что оба шара будут разного цвета.

Ответ: .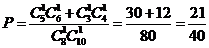

15.7. В урне 4 белых и 5 черных шаров. Из урны взяли три шара. Какова вероятность того, что шары будут одного цвета?

Ответ: .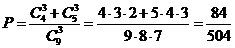

При различных подходах к вероятности, величина P(A) может трактоваться по-разному. На практике часто используются статистическое определение вероятности, т.е. под вероятностью события A понимается величина

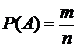, (15.2)

где под n понимается количество наблюдений результатов эксперимента, в которых событие A встречалось ровно m раз (конечно, число наблюдений n должно быть достаточно большим).

Пример 15.3. Аналитик по инвестициям собирает данные об акциях и отмечает, выплачивались ли по ним дивиденды и увеличивались или нет акции в цене за интересующий его период времени. Собранные данные были представлены в виде таблицы:

Выплата дивидендов	Цена увеличилась	Цена не увеличилась	Итого
Производилась
Не производилась
Итого

Если акция выбрана случайно из набора в 246 акций, то чему равна вероятность того, что: а) она из числа тех акций, которые увеличились в цене; б) по ней выплачены дивиденды; в) по ней не выплачены дивиденды, и она не выросла в цене.

Решение. Используя статистическое определение вероятности, легко получаем:

а) ;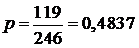

б) ;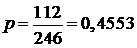

г) .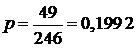

Упражнения

15.8. Статья в журнале «Business Week» обсуждает проблему заработной платы руководителей крупных корпораций. Следующая таблица составлена из данных этой статьи и содержит данные по ряду фирм, в которых руководители имели годовой доход свыше 1 млн. дол. и меньше 1 млн. дол. Таблица составлена в соответствии с тем, получали или нет владельцы акций этих корпораций годовой доход за обсуждаемый период времени.

	Доход руководителя свыше 1 млн. дол.	Доход руководителя меньше 1 млн. дол.	Итого
Держатели акций получили доход
Держатели акций не получили доход
Итого

а) Если фирма выбрана случайным образом, чему равна вероятность того, что её руководитель имеет годовой доход свыше 1 млн. дол.?

б) Если фирма выбрана случайно, чему равна вероятность того, что держатели её акций получили годовой доход?

в) Зная, что некоторая фирма не выплатила дивиденды, чему равна вероятность того, что её руководитель имеет годовой доход свыше 1 млн. дол.?

г) Зная, что руководитель одной из фирм получает свыше 1 млн. дол. годового дохода, чему равна вероятность получения дивидендов держателями акций этой фирмы?

Ответ. а) 0,3; б) 0,7; в) 2/3; г) 1/3.

УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

В задачах, использующих вероятностные количественные характеристики, приходится по вероятностям одних событий оценивать вероятности других событий. Для этого используются различные соотношения, в основе которых лежат теоремы сложения и умножения вероятностей.

Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет; в противном случае такие события называются зависимыми. Например, вероятность события того, что во второй раз из урны, содержащей белые и черные шары, будет вынут белый шар, не зависит от того, какой шар был вынут в первый раз, если он был возвращен обратно. Однако если первый шар не был возвращен обратно, то результат второго извлечения уже будет зависеть от первого, ибо состав шаров в урне уже изменится в зависимости от результата первого извлечения.

Вероятность произведения независимых событий A и B равна произведению вероятностей этих событий:

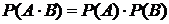. (16.1)

Пример 16.1. Алмазы, возможно, вскоре станут использовать в качестве полупроводников в спутниках связи. Эксперты предсказывают, что алмазные микросхемы будут более быстродействующими, термо- и радиационностойкими, что особенно важно для приборов, работающих в космосе. По оценкам экспертов, вероятности этих трех событий равны 0,9; 0,9 и 0,95 соответственно. Предполагается, что обсуждением проекта по разработке алмазных микросхем стоит вести лишь в том случае, если имеется хотя бы 70% уверенности в том, что они будут обладать всеми тремя указанными свойствами. Должен ли обсуждаться проект?

Решение. Пусть A – событие, состоящее в том, что алмазные микросхемы будут более быстродействующими, B – событие, состоящее в том, что алмазные микросхемы будут более термостойкими, C – событие, состоящее в том, что алмазные микросхемы будут более радиационностойкими. Поскольку события A, B и С независимы, то, используя теорему умножения вероятностей (2.3), получим

.

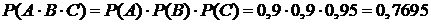Таким образом, поскольку 0,7695>0,7, то предложенный проект следует обсуждать.

Пример 16.2. Дана электрическая цепь:

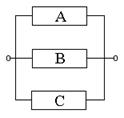
Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.

Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдут из строя все элементы цепи, т.е. и элемент А, и элемент В, и элемент С. При помощи алгебры событий разрыв цепи можно описать следующим образом: 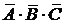. Поскольку эти события независимы, то

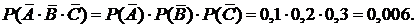
Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается 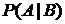или .

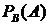Вероятность произведения двух событий A и B равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже имело место:

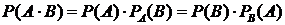. (16.2)

Пример 16.3. Одна из наиболее сложных проблем рыночных исследований – отказ потребителей отвечать на вопросы о потребительских предпочтениях, либо, если опрос проводится по месту жительства, – отсутствие их дома на момент опроса. Предположим, что исследователь рынка с вероятностью в 0,94 верит, респондент согласится отвечать на вопросы анкеты, если окажется дома. Он также полагает, что вероятность того, что этот человек будет дома, равна 0,65. Имея такие данные, оцените процент заполненных анкет.

Решение. Пусть A – событие того, что респондент окажется дома. Вероятность этого события 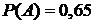. Пусть B – событие того, что респондент согласится отвечать на вопросы. По условию задачи задана условная вероятность 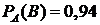, т.е. вероятность того, что он согласится отвечать на вопросы, если он будет дома. Тогда, согласно теореме умножения вероятностей зависимых событий (2.4), вероятность того, что человек будет дома и согласится отвечать на вопросы, будет равна

,

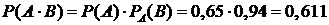т.е. процент заполненных анкет будет равен 61%.

Пример 16.4. Вероятность попадания в цель при отдельном выстреле (событие А) равна 0,8. Какова вероятность поражения цели, если в 2% случаях бывают осечки, т.е. в 2% случаях выстрела не происходит?

Решение. Пусть событие В состоит в том, что выстрел произошел, тогда событие 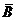означает противоположное событие, т.е. что произошла осечка. По условию P( 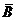)=0,02, отсюда получаем P(B)=1–P( 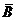)=0,98. По условию задачи P_B(A)=0,8. Поражение цели означает совмещение событий В и А, т.е. что выстрел произойдет и даст попадание. Поэтому

P(AB) = P(B)P_B(A) = 0,98×0,8 = 0,784.

Пример 16.5. В коробке девять одинаковых радиоламп, три из которых были в употреблении. В течение рабочего дня мастеру для ремонта пришлось взять две радиолампы. Какова вероятность того, что обе радиолампы были в употреблении?

Решение. Вероятность того, что первая взятая радиолампа была в употреблении (событие А), равна P(A)=3/9. После того как событие А произошло в коробке осталось 8 радиолам, из которых две были в употреблении. Поэтому для события В, состоящего в том, что вторая радиолампа была в употреблении, условная вероятность P_A(B)=2/8. Следовательно, вероятность появления двух ламп, бывших в употреблении, равна:

P(AB) = P(A)P_A(B) = .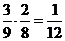

Заметим, что данную задачу можно решить и комбинаторным способом:

P(AB) = .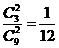

Понятие условной вероятности позволяет естественным образом определить независимость событий. Говорят, что событие А независимо от события В, если имеет место равенство

P_B(A) = P(A),

т.е. если наступление события В не влияет на вероятность наступления события А. Если событие А не зависит от В, то и событие В также не зависит от А. Таким образом, свойство независимости взаимно. Поэтому за определение независимости двух событий А и В можно принять условие (16.1).

Упражнения

16.1. Вероятность того, что завтра цены на потребительские товары вырастут, равна 0,3; вероятность того, что завтра поднимется цена на серебро, равна 0,2, а вероятность одновременного роста цен на потребительские товары и серебро составляет 0,06. Являются ли цены на потребительские товары и серебро независимыми друг от друга? Поясните ответ.

Ответ. Да, т.к. 0,3×0,2=0,23.

16.2. Иностранная фирма, производящая автомобили, интересуется российским рынком. Для изучения вкусов потенциальных покупателей проводится опрос, в котором выясняются наиболее желательные характеристики автомобиля. Предположим, что результаты опроса показали: 35% потенциальных покупателей в основном оценивают автомобиль по его техническим характеристикам, 50% – по его дизайну, 25% – считают важным и то, и другое. Основываясь на этой информации, ответьте, являются ли два вида предпочтений потенциальных покупателей независимыми друг от друга? Объясните почему?

Ответ. Нет, не являются, т.к. 0,35×0,5¹0,25.

16.3. Аудиторская фирма размещает рекламу в журнале "Коммерсант". По оценкам фирмы, 60% людей, читающих журнал, являются потенциальными клиентами фирмы. Выборочный опрос показал также, что 85% людей, которые читают журнал, помнят о рекламе фирмы, помещенной в конце журнала. Оцените, чему равен процент людей, которые являются потенциальными клиентами фирмы и могут вспомнить ее рекламу?

Ответ. 0,85×0,6=0,51, т.е. 51%.

16.4. Консультационная фирма получила приглашение для выполнения двух видов работ от двух международных корпораций. Руководство фирмы оценивает вероятность получения заказа от фирмы А (событие А) равной 0,45. Также, по мнению руководителей фирмы, в случае, если фирма заключит договор с компанией А, то с вероятностью в 90% компания В даст фирме консультационную работу. С какой вероятностью компания получит оба заказа?

Ответ. 0,45×0,9=0,405.

16.5. Вероятность наступления события А в каждом опыте одинакова и равна 0,4. Опыты производятся последовательно до наступления события А. Определить вероятность того, что понадобится ровно 3 опыта.

Ответ. 0,4×0,4×0,6=0,096.

СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Вероятность суммы несовместных событий A и B равна сумме вероятностей этих событий:

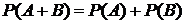. (17.1)

Пример 17.1. В ходе исследования потребительского рынка проводили опрос потребителей. В частности, один из вопросов касался сорта зубной пасты, которую использует потребитель. Если известно, что 14% населения использует сорт A, а 9% – сорт B, то чему равна вероятность того, что случайно выбранный человек будет использовать одну из двух паст. (Предполагается, что в данный момент человек использует только одну пасту).

Решение. Пусть A – событие, состоящее в том, что выбранный человек использует пасту сорта A, а B – событие, состоящее в том, что выбранный человек использует пасту сорта B. Поскольку события A и B несовместные по условию задачи, то, используя теорему сложения вероятностей (2.2), получим

.

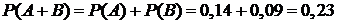Пример 17.2. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение. Введем следующие события: B={появление хотя бы одного туза}, A₁={появление одного туза}, A₂={появление двух тузов}, A₃={появление трех тузов}. Очевидно, что B=A₁+A₂+A₃. Поскольку события A₁, A₂ и A₃.несовместны, то

P(B) = P(A₁)+P(A₂)+P(A₃) =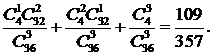

Вероятность суммы совместных событий A и B равна сумме вероятностей этих событий без вероятности их совместного появления:

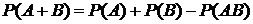. (17.2)

Пример 17.3. Вероятность того, что покупатель, собирающийся приобрести компьютер и пакет прикладных программ, приобретет только компьютер, равна 0,15. Вероятность того, что покупатель купит только пакет программ, равна 0,1. Вероятность того, что будут куплены и компьютер и пакет программ, равна 0,05. Чему равна вероятность того, что будут куплены или компьютер, или пакет программ, или компьютер и пакет программ вместе?

Решение. Пусть A – событие того, что покупатель приобретет компьютер, B – событие того, что покупатель приобретет пакет программ, тогда AB – событие того, что покупатель приобретет и компьютер, и пакет программ. Следовательно, вероятность того, что будут куплены или компьютер, или пакет программ, или компьютер и пакет программ вместе, будет равна

.

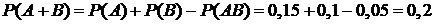Пример 17.3. Два стрелка делают одновременно по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?

Решение. Пусть A₁={первый стрелок попал по цели}, A₂={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А₁+А₂. Поскольку события А₁ и А₂ совместны, но независимы, то

P(А₁+А₂) = P(А₁)+P(А₂)–P(А₁)P(А₂) = 0,7+0,8–0,7×0,8 = 0,94.

Отметим, что событие В можно записать также в виде 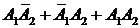. Тогда получим

P(B) = P(A₁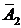)P( )+P( 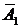)P(A₂)+P(A₁)P(A₂) =
= 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.

Пример 17.4. Дана электрическая цепь:

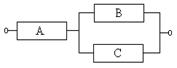
Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.

Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдет из строя элемент А, или сразу два элемента В и С. При помощи алгебры событий разрыв цепи можно описать следующим образом: 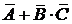. Поскольку эти события совместные и независимые, то получим

= .

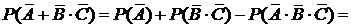
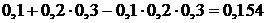Упражнения

17.1. Предположим, что 25% населения живёт в области, охваченной коммерческим TV, рекламирующим новые модели автомобилей некоторой фирмы; 34% населения охвачено коммерческим радио, рекламирующим продукцию той же фирмы. Также известно, что 10% населения охвачено коммерческим и радио и телевидением. Если случайно отобрать человека, живущим в данной области, то чему будет равна вероятность того, что он знаком хотя бы с одной из рекламных передач фирмы?

Ответ. 0,25+0,34–0,1=0,49.

17.2. В большом универмаге установлен скрытый "электронный глаз" для подсчета числа входящих покупателей. Когда два покупателя входят в магазин вместе и один идет перед другим, то первый из них будет учтен электронным устройством с вероятностью 0,98, второй – с вероятностью 0,94, а оба – с вероятностью 0,93. Чему равна вероятность того, что устройство сканирует по крайне мере одного из двух входящих вместе покупателей.

Ответ. 0,98+0,93–0,98×0,93=0,9986.

17.3. Девушка забыла последнюю цифру телефонного номера своего жениха и набрала её наугад. Какова вероятность того, что ей понадобится набирать номер не более трёх раз? Рассмотреть случай блондинки и брюнетки. (Блондинка не помнит какую цифру она набирала перед этим, а брюнетка помнит.)

Ответ. Случай блондинки: ;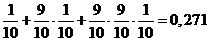

случай брюнетки: 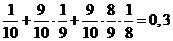.