Свойства размещений и перестановок

Рассмотрим задачи, связанные со свойствами размещений и перестановок.

Пример 6.1. Вычислить

.

Решение. Поскольку

и

,

то

.

Пример 6.2. Упростить выражение

(n ³ 6).

Решение. Поскольку

, ,

,

,

то

.

Пример 6.3. Решить неравенство

.

Решение. Из условия задачи следует, что n³1 и nÎ¥. Поскольку

, ,

то

и данное в условии неравенство равносильно неравенству

.

Пусть n³2, тогда , т.е. 20<15. Противоречие, следовательно, n=1 не является решением данного неравенства.

Пусть n=1, тогда исходное неравенство равносильно следующему

,

Отсюда следует, что первоначальное неравенство имеет три решения:

n₁=3, n₂=4 и n₃=5.

Упражнения

6.1. Вычислить: а) , б) .

Ответ: а) 46, б) 80.

6.2. Упростить: .

Ответ: .

6.3. Решить неравенство .

Ответ: .

6.4. Найти все натуральные n, удовлетворяющие условию:

а) , б) , в) .

Ответ: а) 4, б) 4, в) 10.

6.5. Доказать, что .

СОЧЕТАНИЯ

Пусть опыт состоит в выборе k элементов без возвращения и без упорядочения из некоторого множества, содержащего n элементов. Исходами такого опыта будут подмножества, содержащие k элементов и отличающиеся друг от друга только составом. Получаемые при этом комбинации элементов называются сочетаниями.

Сочетаниями из n элементов по k элементов называются такие комбинации, из которых каждое содержит k элементов, взятых из числа данных n элементов, и которые отличаются друг от друга хотя бы одним элементом.

Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Из этих трёх элементов, в отличие от размещений, можно составить три сочетания по два элемента: ab, ac, bc, ca. Все приведённые сочетания отличаются друг от друга хотя бы одним элементом.

Для иллюстрации различий между сочетаниями и размещениями рассмотрим следующий пример. Пусть выбирается делегация в составе 3 человек из 30 учеников. Здесь, очевидно, не надо учитывать порядок выбранных делегатов, т.к. все члены делегации равноправны. Поэтому каждый такой выбор будет сочетанием из 30 по 3. Однако, выбирая старосту, профорга и физорга из тех же учеников, порядок уже приходится учитывать. В этом случае каждый конкретный результат будет уже размещением из 30 по 3.

Найдем число возможных сочетаний . Чтобы получить размещение из n элементов по k, а их число равно , надо выбрать k элементов из множества, содержащего n элементов, что можно сделать способами, и организовать из них упорядоченное подмножество. Последнюю операцию можно выполнить P_n способами. Таким образом, чтобы получить размещений, надо выполнить две операции, которые можно осуществить и Р_n способами, соответственно. Поэтому, согласно принципу умножения, можно записать

. (7.1)

Отсюда получаем, что число сочетаний будет равно

. (7.2)

Заметим, что , .

Пример 7.1. Сколькими способами можно составить комиссию в составе из трех человек из имеющихся 9 человек, 4 женщин и 5 мужчин, если: а) не важен пол членов комиссии; б) комиссия должна состоять из двух женщин и одного мужчины.

Решение. а) Из смысла задачи следует, что порядок выбора членов комиссии не играет роли. Здесь важен только состав. Тогда выбрать комиссию из трех человек из 9 имеющихся можно

способами.

б) Двух женщин из 4 имеющихся можно выбрать способами, а одного мужчину из 5 можно способами. Тогда общее количество способов выбора комиссии, в соответствии с принципом умножения, можно

способами.

Пример 7.2. Сколькими различных правильных дробей можно составить из чисел 1, 2, 3, 5, 7, 11, 13, берущихся попарно?

Решение. Различных пар из данных чисел, в которых первый элемент меньше второго, будет, очевидно, столько, сколько можно составить сочетаний из 7 по 2:

.

Пример 7.3. Сколько существует делителей числа 210?

Решение. Разложим данное число на простые множители: . Число делителей, составленных из произведения двух простых множителей, равно (а именно числа 6, 10, 14, 15, 21,35); число делителей, составленных из произведения трёх простых множителей, равно 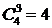(а именно числа 30, 42, 70, 105); число простых делителей равно четырём (а именно 2, 3, 5, 7). Кроме того, делителями являются число 1 и число 210. Итак, согласно принципу сложения, число всех делителей равно

.

Эту задачу можно решить и по-другому. Натуральное число N можно разложить на простые множители следующим образом:

,

a₁, a₂, …, a_n – некоторые натуральные числа. Число p_i может войти в данный делитель с показателем 0, 1, …, a_n – всего a_n+1 способами. Из принципа умножения получаем, что число делителей числа N равно

. (7.3)

Для числа 210 число делителей по формуле (7.3) будет равно (a₁=a₂=a₃=a₄=1)

2×2×2×2=16.

Упражнения

7.1. Сколькими способами можно выбрать 5 делегатов из состава конференции, на которой присутствуют 15 человек?

Ответ: .

7.2. У одного студента есть 11 книг по математике, а другого – 15 книг. Сколькими способами они могут выбрать по 3 книги для обмена?

Ответ: .

7.3. Сколько прямых провести через 8 точек, никакие три из которых не лежат на одной прямой?

Ответ: .

7.4. Найти число диагоналей n-угольника.

Ответ: .

7.5. Компания из 15 человек разделяется на две группы, одна из которых состоит из 6 человек, а другая – из 9 человек. Сколькими способами это можно сделать?

Ответ: .

7.6. В пространстве даны 7 точек, никакие четыре из которых не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти точки?

Ответ: .

7.7. В урне 6 белых и 8 черных шаров. Из нее одновременно вынимают три шара одного цвета. Сколькими способами это можно сделать?

Ответ: .

7.8. В колоде десять карт, из которых три – тузы. Наудачу последовательно вынимается, запоминаются и возвращаются в колоду четыре карты. После каждого возвращения карты колода перемешиваются. Сколько возможно случаев, когда среди вытянутых карт окажется хотя бы один туз?

Ответ: .

7.9. В лаборатории работают 8 физиков и 10 химиков. Надо создать рабочие группы по трем темам. В первую группу должны войти 4 физика, во вторую – 5 химиков, а третья должна состоять из 3 человек, которые могут быть как физиками, так и химиками. Сколькими способами можно создать такие группы?

Ответ:

СВОЙСТВА СОЧЕТАНИЙ

Отметим некоторые свойства сочетаний:

1. (свойство симметрии).

Например,

2. 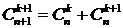(свойство Паскаля).

Данное равенство является рекуррентным соотношением для числа сочетаний. С помощью этого равенства можно составить таблицу для нахождения числа сочетаний. Расположим сочетания в виде треугольной таблицы

Полученную треугольную таблицу принято называть треугольником Паскаля.

3. .

Пример 8.1. Решить уравнение

.

Решение. Поскольку , то получим квадратное уравнение

.

Учитывая, что , получаем решение

.

Пример 8.2. Решить неравенство

.

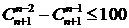Решение. Из условия задачи следует, что n³2 и nÎ¥. Поскольку

, ,

то

.

Таким образом, исходное неравенство равносильно неравенству

.

Поскольку при n=10 получаем , а при n=9 получаем . Учитывая, что n³2 получаем

.

Пример 8.3. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?

Решение. Для звукосочетания клавиши нажимаются одновременно, поэтому для k звуков имеем звукосочетаний. Таким образом, искомое количество есть

.

Учитывая свойство 3, т.е., что

,

получим

.

Упражнения

8.1. Вычислить: а) , б) .

Ответ: а) 81, б) 1.

8.2. Упростить: .

Ответ: 2.

8.3. Найти все натуральные n, удовлетворяющие условию:

а) , б) .

Ответ: а) 3, б) 14.

8.4. Решить неравенство: а) , б) .

Ответ: а) , б) ,

8.5. Доказать, что .

8.6. Имеется 12 различных цветов. Сколькими способами можно составить букет из данных цветов, если в букет должно входить не менее 3 цветов?

Ответ: .