Свойства плотности распределения

1. 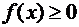для любого хÎ(-¥; +¥).

Доказательство. По определению 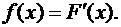По свойству 2 функции распределения F(x)неубывающая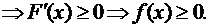

2. Вероятность попадания возможного значения случайной величины Х в заданный промежуток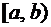

Р(a£ X<b)= 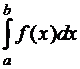.(10.1.2)

Замечание. Из свойства 7 функции распределения (формула (9.2.8)) следует, что для непрерывной случайной величины Х вероятность попадания в произвольный интервал 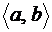(угловые скобки означают, что концы интервала могут входить или не входить в интервал) находится из соотношения

.

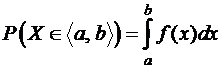3. 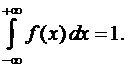(10.1.4)

Доказательство. Положим в равенстве (10.1.2) a=-¥, b=+¥. Тогда

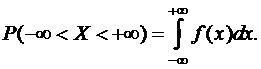
С другой стороны, -¥<C<+¥ есть достоверное событие, следовательно

Р(-¥<C<+¥)=1.

Сравнивая правые части этих равенств, получим (10.1.4).

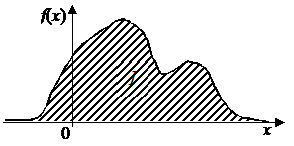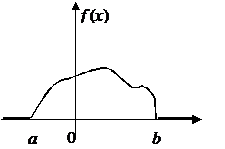Рис. 10.1.2 Рис. 10.1.3

Геометрически равенство (10.1.4) означает, что площадь всего подграфика от -¥ до +¥ равна 1 (рис. 10.1.2).

Замечание. Равенство (10.1.4) является необходимым и достаточным условием того, чтобы неотрицательная функция f (x) являлась плотностью распределения некоторой непрерывной случайной величины.

Следствие.Если плотность сосредоточена на промежутке 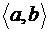, т.е. вне промежутка f(x)=0 (рис. 10.1.3), то

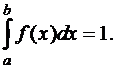(10.1.5)

В данном случае площадь подграфика от а до b равна 1.

Вероятностный смысл плотности распределения.

Физический аналог плотности

Найдём вероятность попадания возможного значения непрерывной случайной величины в малый интервал Dх=х-х₀. По формуле (9.2.7) (свойство 5 функции распределения)

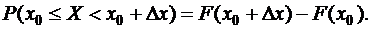(10.2.1)

Разделим обе части этого равенства на Dх:

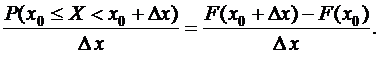
Левая часть этой формулы представляет собой долю вероятности 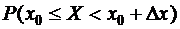, соответствующую единице измерения длины отрезка Dх, т.е. плотность этой вероятности на Dх, или «удельную», «погонную» вероятность.

С другой стороны, из курса дифференциального исчисления известно, что

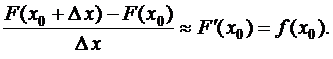
А это по определению и есть плотность вероятности (в точке ).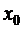

Таким образом, плотность можно интерпретировать как вероятность попадания возможного значения случайной величины в бесконечно малый промежуток, делённую на длину этого промежутка.

Проведём более строгие рассуждения. Рассмотрим равенство (10.2.1). По теореме Лагранжа

,

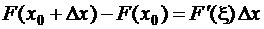где .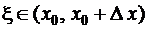

При достаточно малом Dх ,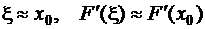

.

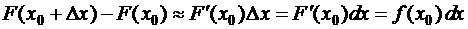Запишем этот результат для любой точки х, учитывая, что Dх=dx:

.

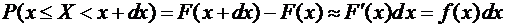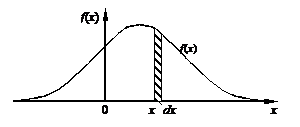Таким образом, для элементарных отрезков длиной dx произведение f (x)dx- это вероятность попадания случайной величины на отрезок dx. Эта вероятность равна площади полоски шириной dx и высотой f(x)(рис. 10.2.6), Рис. 10.2.6

а точнее, .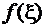

Если проинтегрируем эту полоску по любому промежутку 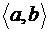, то получим вероятность попадания в этот промежуток (свойство 2 плотности). При интегрировании по всей числовой оси получим единицу (свойство 3).

Замечание.Во всех расчётах с непрерывными случайными величинами дифференциал вероятности f (x)dx, равный 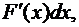играет ту же роль, какую играют вероятности p_i при расчётах с дискретными случайными величинами. Чтобы от формулы для дискретных величин перейти к формуле для непрерывных величин, во многих формулах достаточно будет заменить p_i на f (x)dx и сумму – соответствующим интегралом.

Физическая аналогия плотности распределения – линейная плотность распределения вещества по линии. Известно, что размерность линейной плотности равна кг/м. Пусть имеется бесконечная прямая или отрезок прямой, масса которого равна единице. Из физики известно, что в каждой точке этой прямой плотность вещества определяется следующим образом:

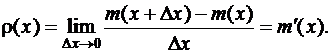
Масса отрезка длиной 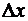равна

.

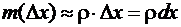Просматривается аналогия между массой и функцией распределения вероятности, между линейной плотностью вещества и плотностью вероятности.