Характеристическая случайная величина (индикатор события)

Рассмотрим серию испытаний по схеме Бернулли. Характеристическая случайная величина c_k – это число появлений события А при k-м испытании. Событие А может произойти в одном испытании либо 1 раз, либо ни разу (0 раз). Следовательно, величина c_k может принимать только два значения: 1, если событие А произойдет при k-м испытании, и 0, если событие А не произойдет при k-м испытании. Т.к. вероятность события А равна р в каждом испытании, то величины c₁, c₂,…, c_n имеют одинаковые таблицы распределения вероятностей:

c1 p q р

c2 p q р

……

ck p q р

……

cn p q р

Характеристическую случайную величину называют также индикатором события, т.к.она показывает, как ведёт себя событие А в каждом испытании (появляется или нет). Запишем значения этой случайной величины аналитически (в виде формулы):

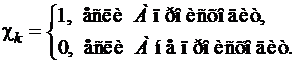(8.2.1)

Полигон индикатора события изображен на рис.8.2.1.

Рис.8.2.1

Биномиальное распределение (распределение Бернулли)

Пример 1. Стрелок производит 2 выстрела по мишени. Вероятность попадания при каждом выстреле =0,4. Построить ряд распределения числа попаданий при двух выстрелах.

Случайная величина Х – число попаданий. Эта случайная величина может принимать следующие возможные значения: х₁=0, х₂=1, х₃=2. Вероятности вычислим по формуле Бернулли

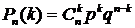(8.3.1)

для n=2, p=0,4, q=0,6:

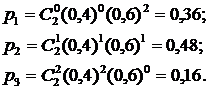
Контроль: 0,36+0,48+0,16=1.

Ряд распределения будет иметь вид:

Х
p	0,36	0,48	0,16

Полигон распределения изображен на рис.8.3.1. Видно, что наиболее вероятно одно попадание из двух выстрелов.

Определение. Случайная величина Xназывается биномиально распределённой с параметрами n и р, если возможные значения k=0, 1,…, n она принимает с вероятностями Р_n(k), задаваемыми формулой Бернулли:

Р(Х=k)= .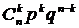

Биномиальное распределение полностью определяется двумя параметрами: n и р.

Применим бином Ньютона для суммы вероятностей р и q. При этом в правой части суммируются вероятности Р_n(k):

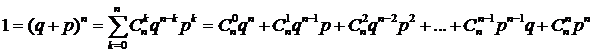. (8.3.4)

Таким образом, закон биномиального распределения имеет вид:

Х			…………	k	…………	n-1	n
p	qn		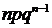…………		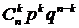…………	n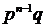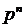

Из формулы (8.3.4) видно, что сумма второй строки таблицы равна 1 (т.к. p+q=1).

Распределение Пуассона

В некоторых задачах физики и техники встречаются случайные величины, подчинённые закону распределения Пуассона. Закону распределения Пуассона подчиняются, например, количество вызовов на автоматической телефонной станции за данный промежуток времени; количество электронов, вылетающих с накалённого катода за данный промежуток времени.

Сделаем важное допущение: произведение np сохраняет постоянное значение, равное l. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остаётся неизменным. Действительно, вероятность приближенно равна относительной частоте: 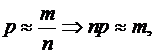т.е. l приближённо равна абсолютной частоте.

Определение.Случайная величина Х называется распределённой по закону Пуассона с параметром l=np, если она принимает значения k=0,1,2,… с вероятностями

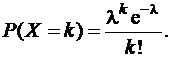(8.4.1)

Составим ряд распределения случайной величины Х:

Х					…	N	…
р					…		…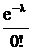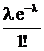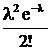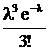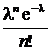

Найдём сумму вероятностей:

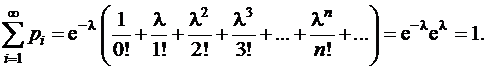
(в скобках получилось разложение функции е^l в ряд Маклорена).

Распределение Пуассона полностью определяется одним параметром l и обладает удобными аналитическими свойствами. Например, сумма двух независимых случайных величин, имеющих распределение Пуассона с параметрами l и m, имеет распределение Пуассона с параметром l+m и используется при построении математических моделей различных случайных процессов. Применяется для описания редких событий.

Пример 1.Вероятность того, что изделие не выдержит испытания, равна 0,001. Построить ряд распределения и полигон случайной величины Х – количества изделий из 5000, не выдержавших испытания.

l=5000×0,001=5.

Р(Х=0)=0,0067 Р(Х=4)=0,1755 Р(Х=8)=0,0653

Р(Х=1)=0,0337 Р(Х=5)=0,1755 Р(Х=9)=0,0363

Р(Х=2)=0,0842 Р(Х=6)=0,1462 Р(Х=10)=0,0181

Р(Х=3)=0,1404 Р(Х=7)=0,1044 Р(Х=11)=0,0082

Р(Х=12)=0,0034.

Кривые (полигоны), вычисленные с помощью биномиального распределения и распределения Пуассона, практически совпадают. Приведём значения вероятностей, вычисленных по биномиальному закону.

р=0,001; q=0,999; n=5000. По формуле (8.3.2)

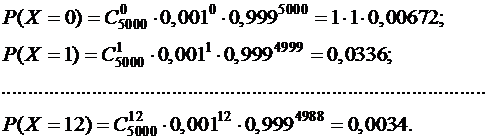
Данное совпадение и должно иметь место, т.к. при больших п, т.к.

®

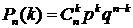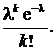
Распределение Пуассона впервые было исследовано французским ученым С.Пуассоном в 1837 г.