Составление программ. Глобальные и локальные переменные

Рассмотрим вопросы составления программ. Простейшая программа может представлять собой заключенную в скобки последовательность операторов, разделенных знаком “;”. Подобная программа дана в примере 8.3. Рассмотрим еще один пример.

Пример 8.8.

Составим программу для вычисления значения экспоненты с заданной точностью. Будем последовательно вычислять сумму членов Маклорена до тех пор, пока очередное слагаемое не станет меньше допустимой погрешности. Для этого напишем следующую программу:

In[ ] :=ex[x_, eps_] := ( For[ u=1.; e=1.; k=1, Abs[u]>eps, u=u*x/k; e=e+u; k++ ]; e)

Если мы теперь напишем вопрос: In[ ] :=ex[1., 10^-5], то получим ответ: Out[ ] = 0.367882. Можем убедиться, что погрешность действительно не превышает 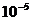, вычислив разность:

In[ ] :=ex[1, 10^-5] - EOut[ ] =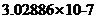

В программах подобного типа все переменные являются глобальными. Их значения доступны из любого места рабочего документа. Например, на вопрос In[ ] :=kполучим ответ“10” – количество членов ряда, обеспечивающее в данном случае требуемую точность.

Наличие глобальных переменных таит в себе возможность ошибки из-за конфликтов между значениями переменных. Поэтому более надежный путь – создание программ с локальными переменными. Синтаксис такой программы:

Module[{x, y, …}, expr].

В этом выражении {x, y, …} – список локальных переменных, expr – тело программы. Список может включать инициализацию переменных: {x=x0, y=y0,…}. Названия локальных переменных могут совпадать с именами глобальных, так как при каждом обращении к программе вместо объявленных локальных имен создаются новые имена. Тело программы может включать несколько команд. Каждая команда за исключением последней, включающей результат работы программы, отделяется от последующей точкой с запятой. (Вспомним, что точка с запятой является знаком запрета вывода результата.)

Использование локальных и глобальных переменных проиллюстрируем следующим примером рабочего сеанса. Введем вначале глобальную, а затем локальную переменную с тем же именем. In[1] := t=5;

In[2]:= Module[ {t=10}, t ]Out[2] = 10

Глобальная переменная сохраняет свое значение:

In[3] := tOut[3] =5

Введем локальную функцию с тем же именем t:

In[4] := f[x_] := Module[ {t}, t[x] = x^2 ]

In[5] := f[x]Out[5] = x²

Можно убедиться, что глобальная переменная t по-прежнему сохраняет свое значение

Пример 8.9.

Преобразуем программу вычисления экспоненты. Поскольку инициирование значений локальных переменных проведем при их объявлении, то вместо цикла For будем использовать цикл While.

In[] := ex1[x_, eps_] := Module[ {w=1., s=1., i=1}, While[ Abs[w]>eps, w=w*x/i; s=s+w; i++ ]; s ]

В этой программе все переменные являются локальными.

Пример 8.10.

Вычисление квадратного корня числа “x” с помощью процесса Герона. Алгоритм представляет собой итерационный процесс. Сначала задается некоторое начальное приближенное значение, например, y₀ = x +1. Затем это значение уточняется в ходе последовательных итераций по формуле: y_n+1 = (y_n + x/y_n)/2. Процесс вычислений заканчивается, если два последующих значения отличаются не более чем на величину допустимой погрешности. Поскольку при данном выборе начального значения процесс итераций описывает монотонно убывающую последовательность: y₀ > y₁ > y₂ > … , – то нет необходимости в использовании функции Abs[ ]. Программа имеет вид:

In[ ] := root2[x_, eps_] := Module[ {u, v},

For[ u = x + 1.; v = (u + x / u) / 2, u –v > eps, u = v; v = (v + x / v) / 2 ]; v ]

Примеры более сложных программ приведены в приложении.

Прерывание вычислений

Часто возникает необходимость прерывания вычислений. Для этого в пакете Математика можно использовать следующие функции.

Abort[ ]– так же, как и одноименная команда меню, останавливает все вычисления. Команда может быть использована в любом месте программы.

Пример 8.11. Введем функцию, которая вычисляет двоичный логарифм x, если выполнено условие: x>0, и печатает предупреждение об ошибке, если это условие нарушено:

In[ ] := f1[x_] := If[ x>0, Log[ 2., x], Print["Error: x<=0!"]; Abort[ ]]

In[ ] := f1[ 8]Out[ ] = 3.

In[ ] := f1[-8]Out[ ] = Error: x<=0! $Aborted

Break[ ]– обеспечивает экстренный выход из ближайшего охватывающего цикла Do, For или While. (Применение оператора Break[ ] см. в примере 7.2.)

Goto[tag] –передает управление в точку программы, отмеченную меткой Label[tag];. Фрагмент программы с передачей управления может выглядеть следующим образом:

If[ test, Goto[ abc ]];

…

…;

Label[ abc ]; …–

если выполнено условие test, управление передается в точку, помеченную меткой abc.

Пример использования функции Goto имеется в приложении (см. программу перемножения матриц).

Списки

9.1. Создание списков. Обращение к элементам списков

Список представляет собой набор каких-либо элементов и может рассматриваться как обобщение понятия массива. В отличие от массива список может включать в себя элементы разных типов. Списки относятся к наиболее гибким и продуктивным объектам Математики.

Наиболее простой способ определить список – дать перечисление его элементов в фигурных скобках. Элементы списка отделяются запятыми. Однако элемент, после которого стоит точка с запятой, не выводится на экран и не включается в список – данный элемент сохраняется в памяти вне списка.

Пример 9.1. Сформируем список разнородных элементов:

In[ ] := L1={f[x_]=x^2; "список", 0.5, a+b, {x,y}}Out[ ] = {список,0.5,a+b,{x,y}}

Первый из элементов – функция f – отсутствует в списке, однако сохраняется в памяти:

In[ ] :=f[y]Out[ ] = y²

Обратим внимание, что последний элемент списка L1 сам является списком.

Выделить из списка List элемент с номером n можно с помощью команд:

Part[List,n] или List[[n]].

Отметим, что нумерация элементов списка начинается с единицы.

Новый список, составленный из элементов списка List, можно получить с помощью команд:

Part[List,{n1,n2,..}] или List[[{n1,n2,..}]], –

где n1, n2,.. – номера нужных элементов.

С выделенными элементами можно производить любые допустимые операции

Пример 9.2. Примеры обращения к элементам списка L1:

In[ ] :=L1[[{4, 2}]]Out[ ] = {{x,y}, 0.5}

– список, включающий четвертый и второй элементы списка L1.

In[ ] :=L1[[4, 2]]Out[ ] = y

– обращение ко второму подэлементу четвертого элемента списка L1.

In[ ] :={L1[[2]], L1[[2]]^2, L1[[2]]*3}Out[ ] = {0.5, 0.25, 1.5}

– действия со вторым элементом списка L1.

В тех случаях, когда значения элементов списка подчиняются какому-либо закону, для создания списка можно воспользоваться одной из стандартных функций пакета Математика.

Range[nmin, nmax, dn] –созданиесписка чисел N=nmin+dn*i, i=0,1,..,imax, где imax равно целой части числа (nmax-nmin) / dn (отметим, что шаг dn может быть отрицательным).

Table[f, {i, imin, imax, di}] – создание одномерного списка значений функции f.

Значения imin и di можно не указывать, если эти значения равны единице. Если значения функции не зависят от индекса, то и индекс можно не указывать; в этом случае в фигурных скобках указывается только длина списка. Функция f также может быть списком. Функция Table позволяет создавать также списки аналитических выражений.

Table[f, {i, imin, imax}, {j, jmin, jmax},..] – создание двумерного списка.

Пример 9.3. Построим списки, используя функции Range и Table:

In[ ] :=v1=Range[5, -5, -7]Out[ ] = {5, -2}.

In[ ] :=v2=Table[Random[Integer, {-9, 9}], {3}]Out[ ] = {4, 0,-3} – один из возможных ответов.

In[ ] :=m1=Table[Abs[i -j]+1, {i, 2}, {j, 2}]Out[ ] = {{1, 2}, {2, 1}}.

Отметим, что списки v1 и v2, по существу, являются векторами, а список m1 является матрицей. Представим m1 в виде матрицы: In[ ] :=m1//MatrixFormOut[ ] =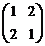

Поскольку векторы в пакете Математика представляются списками, то вектор-столбец и вектор-строка – неразличимы.

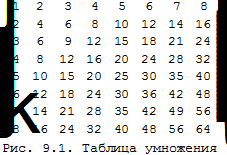
Пример 9.4. Команда In[ ] :={ Table[i*j, {i, 8}, {j, 8}]//MatrixForm,

" Рис. 9.1. Таблица умножения " }//TableForm

создает список, включающий фрагмент таблицы умножения и подпись под таблицей. Таблица умножения cоздается с помощью функции Table и выводится на экран в виде матрицы. Функция TableForm размещает в столбик элементы списка. Результат виден на рис. 9.1.

9.2. Преобразование списков

Пакет Математика содержит большой набор функций для преобразования списков:

Drop[List, n] –вычеркивание первых n элементов из списка List;

Drop[List, -n] –вычеркивание последних n элементов из списка List;

Prepend[List, el] –добавление элемента el в начале списка List;

Append[List, el] –добавление элемента el в конце списка List;

Insert[List, el, n] –вставка элемента el на n-е место в списке List;

Join[List1, List2,…]или List1 ~Join~ List2~… –объединение списков;

ReplacePart[List, el, n]или List[[n]] = el –замена n-го элемента списка List на элемент el;

Sort[List] –упорядочивание элементов списка List;

RotateLeft[List, n], RotateRight[List, n} –циклическая перестановка списка List на n элементов влево и вправо.

Пример 9.5. Преобразуем введенный ранее список L1={"список", 0.5, a+b, {x,y}}:

In[ ] :=Drop[L1, 2]Out[ ] = {a+b, {x, y}}

In[ ] :=RotateLeft[L1, 1]Out[ ] = {0.5, a+b, {x, y}, список}

In[ ] :=L2=Join[ L1, Table[a^n, {n, -1, 2}]]Out[ ] = {список, 0.5, a+b, {x+y}, 1/a, 1, a, a²}

In[ ] :=Sort[L2]Out[ ] = {0.5, 1, список, 1/a, a, a², a+b, {x+y}}

Функция Total.

Для одномерного массива list функция Total[list] вычисляет сумму элементов массива.

Для двумерного массива функция Total[{{x₁, y₁, …}, {x₂, y₂, …}, …} порождает список сумм:

{Total[{x₁, x₂, …}], Total[{y₁, y₂, …}], …}.

Для произвольного списка функция Total[list, n] дает сумму всех элементов вплоть до уровня n.

Отметим, что команды Total[list] и Total[list,1] являются одной и той же командой.

Пример 9.6. Создадим список, второй элемент которого сам является списком:

In[ ] :=L3={a,{x,y,z}};

Применим двумя способами функцию Total:

In[ ] :=Total[L3]Out[ ] = {a+x, a+y, a+z}

In[ ] :=Total[L3, 2] Out[ ] = a+x+y+z

Функция Total вычисляет сумму во много раз быстрее, чем функция Plus.

Пример 9.7. Создадим массив из 10⁶ случайных чисел: In[ ] :=t=Table[Random[], {1000000}];

Сравним время вычисления суммы чисел массива t с помощью функций Total и Plus:

In[ ] :=Total[t]//TimingOut[ ] = {0.047, 499855.}

In[ ] :=Apply[Plus, t]//TimingOut[ ] = {4.5, 499855.}

Видим, что суммирование с помощью функции Plus требует почти в 100 раз больше времени.

Не будем хранить в памяти такую большую таблицу: In[ ] :=Clear[t].

Матричные функции

Создать матрицу – это значит каким-либо способом создать двумерный массив. Подобным образом получена матрица m1 в примере 9.3. Функции для создания специальных матриц:

IdentityMatrix[n]– порождает единичную матрицу ;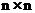

DiagonalMatrix[list]– дает диагональную матрицу с элементами списка list на главной диагонали.

Функции для работы с матрицами.

MatrixForm[m]– выводит на печать двумерный массив m в виде матрицы.

MatrixForm[v]– выводит на печать одномерный массив v в виде вектора-столбца.

Dot[m1,m2] или m1.m2– вычисляет произведение матриц.

m1*m2 –производитпоэлементное перемножение матриц.

Inverse[m]– вычисляет обратную матрицу.

Transpose[m]– производит транспонирование.

MatrixPower[m, n]– возводит матрицу m в степень n.

Det[m] – вычисляет определитель матрицы.

Length[m] – определяет число строк матрицы.

Dimensions[m] – определяет размеры матрицы m.

Eigenvalues[m] – вычисляет собственные значения матрицы.

Eigenvectors[m] – находит собственные векторы матрицы m.

MatrixRank[m]– подсчитывает ранг матрицы.

Tr[m] – вычисляет след матрицы – сумму диагональных элементов.

Norm[v] –подсчитывает длину вектора v: 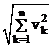, где v _k – компоненты вектора.

Norm[v, ¥] – вычисляет норму вектора по формуле .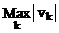

Norm[m, ¥]– вычисляет норму матрицы m по формуле .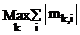

Norm[m, 1] –вычисляет норму матрицы по формуле .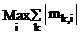

Отметим, что матричные функции включают также аналитические преобразования.

Пример 9.8. Действия с матрицами.

Введем матрицу m2 и вектор v3: In[ ] := m2={{-1, 4}, { 2, -3}}; v3={- 4, 3};

Длина вектора: In[ ] := Norm[v3]Out[ ] = 5

Норма вектора: In[ ] := Norm[v3, ¥]Out[ ] = 4

Определительматрицы: In[ ] := Det[m2]Out[ ] = -5

Норма матрицы: In[ ] := Norm[m2, ¥]Out[ ] = 5

Собственные значения и собственные векторы матрицы m1:

In[ ] := Eigenvalues[m2]Out[ ] = {-5, 1}

In[ ] := Eigenvectors[m2]Out[ ] = {{-1, 1}, {2, 1}}

Произведение матрицы на вектор: In[ ] := m2.v3Out[ ] = {16, -17}

Обратная матрица: In[ ] := m3=Inverse[m2]Out[ ] =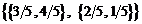

Произведение исходной матрицы на обратную: In[ ] :=m2.m3Out[ ] = {{1, 0}, {0, 1}}

Объединим матрицы m1 и m3 в единую матрицу :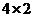

In[ ] :=m4=Join[m2, m3]Out[ ] =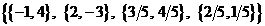

Транспонируем матрицу m4:

In[ ] :=m5=Transpose[m4]Out[ ] =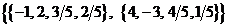

Просуммируем элементы столбцов матрицы m5: In[ ] :=Total[m5]Out[ ] =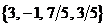

Просуммируем все элементы матрицы m5: In[ ] :=Total[m5, 2]Out[ ] = 4

Создадим диагональную матрицу: In[ ] :=DiagonalMatrix[v3]Out[ ] = {{-4, 0}, {0, 3}}

Ряд функций для преобразования списков приведен также в разделах 11 и 12.

В заключение раздела приведем пример определения векторной функции. Данная функция реализует операцию “бабочка” – базовую операцию алгоритма быстрого преобразования Фурье. Операция вычисляет дискретное преобразование Фурье для массива из двух элементов {a, b}; в результате операции исходный массив преобразуется в массив {a+b, a-b}:

In[ ] := w[{a, b}] := {a+b, a-b}; w[{1, 2}] Out[ ] = {3, -1}

Математика сначала вычисляет целиком вектор, описанный в правой части операции присваивания, и затем заменяет старый вектор на новый.

Массивы

В пакете Математика имеется возможность создавать массивы из символических элементов. Эти массивы можно использовать в аналитических формулах, которые будут справедливы при любом выборе компонент массивов.

Команда Array[a, m] создает вектор из m элементов.

Команда Array[a, {m, n}] создает матрицу .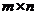

Пример 10.1

Создадим вектор из двух компонент и изменим знак второй компоненты:

In[ ] := V=Array[v,2]; V[[2]]=-V[[2]];

Проведем несколько операций с вектором V: запишем его в виде вектора-столбца, найдем евклидову норму, найдем скалярное и поэлементное произведение вектора самого на себя и, наконец, возведем вектор в степень n.

In[ ] := {V//MatrixForm, Norm[V], V.V, VV//MatrixForm, V^n//MatrixForm}

Out[ ] =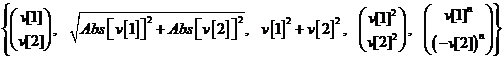

Создадим матрицу 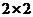и выведем ее на экран в исходном и транспонированном виде:

In[ ] := M=Array[m,{2,2}]; {M//MatrixForm, Transpose[M]//MatrixForm}

Out[ ] =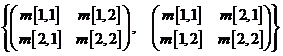

Найдем определитель и след матрицы:

In[ ] := Det[M]

Out[ ] = -m[1,2] m[2,1]+m[1,1] m[2,2]

In[ ] := Tr[M]

Out[ ] = m[1,1]+m[2,2]

Найдем произведение матрицы на вектор по правилу “строка на столбец”, а также поэлементное произведение:

In[ ] := M.V//MatrixForm

Out[ ] =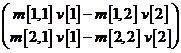

In[ ] := M 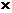V//MatrixForm

Out[ ] =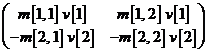

Основные типы графиков

Двумерные графики

Plot[{f₁, f₂, …}, {x, xmin, xmax}] – график одной или нескольких функций, заданных формулами, на отрезке от xmin до xmax.

ListPlot[{{x₁, y₁}, {x₂, y₂},…}] – график списка точек с координатами (x, y). Если x принимает натуральные значения: x_i=i, i=1, 2, 3, …, – то значения x могут быть опущены.

ListPlot[{list₁, list₂, …}] – график нескольких списков точек. Размер точек можно задать с помощью опции: PlotStyle->PointSize[0.03].

ParametricPlot[{{x₁(t), y₁(t)}, {x₂(t), y₂(t)}, …}, {t, tmin, tmax}] – график функций, заданных параметрически.

PolarPlot[{r₁, r₂, ..}, {j, j _min, j _max}] – график функций в полярных координатах.

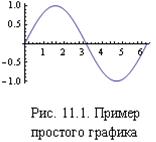
Для того, чтобы построить двумерный график, например, график функции Sin[x] на отрезке [0, 2p], достаточно написать простую команду:

In[ ] := p1=Plot[Sin[x], {x, 0, 2Pi}]

Полученный график показан на рис. 11.1. Данному графику присвоено имя p1. Имя не является обязательным элементом команды. Имя нам нужно только для того, чтобы рассмотреть свойства графика. Напишем команду:

In[ ] := Options[p1]

Запустив команду на счет, получим список значений опций, установленных по умолчанию:

Out[]=

{AspectRatio->1/GoldenRatio, Axes->True, AxesOrigin->{0,0}, PlotRange->{{0, 2Pi},{-1.,1.}},

PlotRangeClipping->True, PlotRangePadding->{Scaled[0.02],Scaled[0.02]}}

Помимо установок по умолчанию имеется много дополнительных возможностей для изменения свойств графиков. Подробное описание всех опций можно найти в разделе Справка (Help). Остановимся только на некоторых из опций.

PlotRange – задает диапазон изменения координаты y. Например, PlotRange->All – вывод всего диапазона изменений y, PlotRange->{0, 1} – вывод на график только значений y в пределах от 0 до 1.

AspectRatio – задает отношение длины оси y к длине оси x. По умолчанию, это отношение задается в пропорции “золотого сечения”. Это приводит к тому, что круг превращается в эллипс, квадрат – в прямоугольник и т.п. Отношение длин осей может быть задано произвольным числом. Если задана опция AspectRatio –> Automatic, то отношение длин осей подсчитывается автоматически из условия равенства масштабов по обеим осям. Значение AspectRatio –> Automatic необходимо использовать, если требуется сохранить неискаженные пропорции изображаемых фигур.

Замечание. Для параметрических, полярных графиков и примитивов по умолчанию устанавлены одинаковые масштабы по осям координат.

Опция GridLines –> Automatic вводит линии сетки.

Некоторые из опций изучим в процессе их применения.

Пример 11.1.

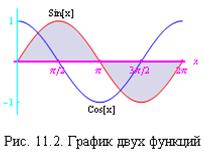
Напишем команду для вывода графика двух функций:

In[ ] :=Plot[ {Sin[x], Cos[x]}, {x, 0, 2Pi}, PlotStyle ->{RGBColor[1, 0, 0], RGBColor[0, 0, 1]},

PlotRange ->{-1.3, 1.3}, Prolog ->Text["Sin[x]",Scaled[{0.28, 0.96}]],

Epilog -> Text["Cos[x]",Scaled[{0.51, 0.04}]], AxesLabel ->{x, None},

Ticks->{ {{p/2, "p/2"}, {p, "p"}, {3p/2, "3p/2"},

{2p, "2p"}}, {{-1, "-1"}, {1, "1"}} },

AxesStyle->{{RGBColor[1,0,1],Thickness[0.01]},{RGBColor[0,1,1],Thickness[0.01]}},

Filling->{1->Axis}]

Изображаемые функции запишем в виде списка: {Sin[x], Cos[x]}. Раскрасим графики этих функций в разный цвет, используя опцию PlotStyleи функцию RGBColor. Выберем диапазон изменения координаты y от -1.3 до 1.3 так, чтобы осталось место для подписей к графикам. Для создания подписей используем опции Prolog и Epilog и функцию Text. Второй аргумент функции Text задает координаты центра подписи. Слово Scaled означает, что используются относительные координаты: за единицу принимается размер рисунка вдоль соответствующей оси, а координаты отсчитываются от нижнего левого угла рисунка. С помощью опции AxesLabel поставим метку у оси x. Используя опцию Ticks, промаркируем оси координат. Раскрасим оси координат. С помощью функции Thickness сделаем оси утолщенными. С помощью опции Filling->{1->Axis} заполним фоном пространство между графиком функции Sin[x] и осью x. В итоге получим график, показанный на рис. 11.2.

Пример 11.2.

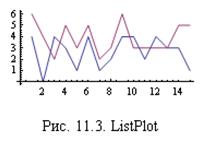
Построим график двух случайных последовательностей точек:

In[ ]:=ListPlot[{Table[Random[Integer, {0,4}], {15}],

Table[Random[Integer, {0,4}]+2, {15}]},

Joined->True, AspectRatio->Automatic]

Соединим точки отрезками прямых линий (опция Joined->True). График показан на рис. 11.3.

11.2. Функции Showи GraphicsArray. Графические примитивы.

Функция GraphicsArray формирует одномерный или двумерный массив графиков. Формат функции:

GraphicsArray[{g₁, g₂,…}]или GraphicsArray[{{g₁, g₂,…},…}],

В первом случае выводится ряд, а во втором – двумерный массив графических объектов g₁, g₂,…. Один массив может объединять графики разных типов: двухмерные, трехмерные, параметрические и др.

Массивы графиков выводятся с помощью функции Show. Функцию Show можно рассматривать как аналог функции Print, применяемый к графикам. Формат функции при выводе массивов графиков:

Show[GraphicsArray[{g₁, g₂,…}], options]

Функция Show позволяет также выводить в единых координатах разные графические объекты, например, графики разных типов или разные графические примитивы. Формат функции в этом случае: Show[graphics, options], где graphics – список выводимых графических объектов.

Опции функции Show – это графические опции. Если опции функции Show указаны явно, то их значения заменяют собой значения опций, указанных для отдельных графиков.

Пакет Математика включает ряд готовых двухмерных и трехмерных фигур – примитивов. Остановимся только на некоторых из них:

Point[{x, y}], Point[{x, y, z}]; – точка на плоскости или в трехмерном пространстве;

Line[{{x₁, y₁},…}] – ломаная линия на плоскости или в пространстве;

Polygon[{{x₁, y₁},…}] – заполненный многоугольник на плоскости или в пространстве;

Rectangle[{xmin, ymin}, {xmax, ymax}] – заполненный прямоугольник;

Circle[{x, y}, r] – окружность радиуса r с центром в точке (x, y);

Disk[{x, y}, r] – заполненный круг r с центром в точке (x, y);

Text[ expr, {x, y}] – текст expr, центр которого находится в точке (x, y).

Пример 11.3.

Построим массив графиков, включающий окружность, прямоугольник и круг (рис.11.4).

In[ ] := a=Graphics[Circle[{0, 0}], BaseStyle->Hue[1]];

b=Graphics[Rectangle[{-1, -1}, {1, 1}],

AspectRatio->1/GoldenRatio];

c=Graphics[Disk[{0, 0}], BaseStyle->Hue[0.5]];

Show[GraphicsArray[{a,b,c}]]

С помощью опции AspectRatio->1/GoldenRatio превращаем квадрат в прямоугольник “черный квадрат”. Опцию BaseStyle –>Hue[..] используем для окраски фигур. С помощью функции Show выводимна экран массив графиков. Точку с запятой используем для запрета вывода графиков по-отдельности.

Пример 11.4.

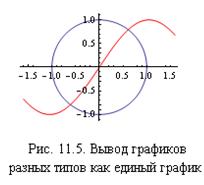
Построим в единых координатах два графика разных типов: график окружности в полярных координатах и обычный график функции Sin[1.5 x].

In[ ] := pc=PolarPlot[1, {fi, 0, 2Pi},

PlotRange->{{-1.6, 1.6}, {-1.1, 1.1}}];

ps=Plot[Sin[1.5 x], {x, -1.6, 1.6}, PlotStyle->Red];

Show[{pc,ps}]

Для вывода графиков разных типов используем функцию Show. Совместный график показан на рис. 11.5.