Понятие предиката. Конъюнкция,дизъюнкция,отрицание,импликация и эквиваленция предикатов, их мн-ва истинности.

Предикат-это предложение с одной или несколькими перемен-ми и кот при конкрет-х значениях перемен-х превращ-ся в высказыв-е. по числу переменных, входящих в предикат выделяют: одноместные, двуместные и т д. предикаты. С каждым предикатом связаны 2 мн-ва: 1-мн-во определения предиката (обознач-ся х-это мн-во тех значений переменной, при кот предикат обращ в высказывание); 2-мн-во истинности предиката-это мн-во тех знач переменной из области определения при кот предикат превращается в истинное высказывание Т 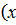. обноместные преликаты обозн А(х), х 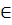Х(читается- на мн-ве А задан предикат) (напр. А(х): число х-простое). 2 предиката А(х) и В(х) заданные на одном и том же мн-ве х наз-ся равносильным (эквивалентным), если они имеют одно и тоже мн-во истинности и запис-ся А(х) 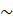В(х).(напр А(х):х+2=4, х 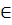N; В(х): 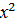-4=0,х 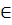N. 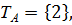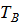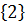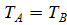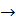= , А(х) 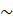В(х)). Предикаты: элементные, составные. Состав-е образовыв-ся из элементарных при помощи логически связанных высказываний.

Отрицанием предикатов. Пусть на множ х задан предикат А(х), отрицанием предиката А(х) наз предикат 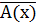заданный на том же множ х , а множ истенности индиката 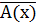это те значения хєХ для которых А(х). =

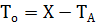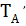
Конъюнкцией А(х) и В(х) наз-ся составной предикат А(х) и В(х) заданный на том же мн-ве х. Он истинен когда одновременно истинны оба предиката А(х) и В(х). Мн-во истинности конъюнкции предиката А(х) и В(х) явл перечисление мн-в истинности предикатов.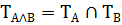

Дизъюнкцией наз-ся составной предикат А(х) и В(х) задан на том же мн-ве х. А(х) 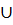В(х) / А(х) или В(х), х 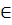Х. он истинен тогда, когда хотя бы 1-н из предикатов истинен.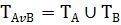

Импликацией наз-ся составной предикат А(х) 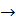В(х), ели А(х), то В(х) задан на том же мн-ве х. Он ложен когда А(х)-И, а В(х)-Л, при остальных И. Из формулы А 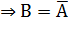v В можно получить следующую формулу для вычисления множ истинности импликации: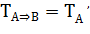

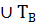
Эквиваленцией наз-ся составной предикат А(х) 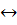В(х), х 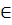Х. Истинно только когда оба И или оба Л, при остальных ложно. 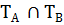и ;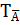

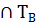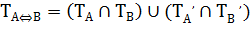
7. Матем-е понятия. Объем и содерж-е понятия. Способы определения понятий. Требования к определению понятий.

Объем понятия-это мн-во объектов, обозначаемых одним и тем же термином. Если объем понятия А явл частью объема понятия В ( 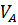) ) 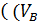понятие А наз-т видовым по отношению к понятию В, а понятие В родовым по отношению к А (напр. Понятие ромб явл видовым понят-м параллелограмма, а понятие параллелограмм это родовое понятие для ромба). Если все объекты, которые входят в объем данного понятия обладают некоторыми свойствами, то это свойство наз существенными (без него объект не может существовать)

Содерж-е понятия-это указание существенных свойств объекта которых достаточно для распознания объекта.. М/у объемом и содерж-м понятия сущ-т связь:чем больше объем понятия, тем меньше его содержание. Чем больше содержание тем меньше его объем. Понятие-логич-я операция, кот раскрывает содержание понятия. Осн сп-бы определения понятий:1) определение понятия ч/з род и видовое отличие. При этом способе указыв-ся более общее родовое понятие, а затем указыв-ся видовое отличие, то св-во кот выделяет данный вид из других видов данного рода. Определение понятия = родовое понятие + видовое понятие (напр. Квадрат=это прямоугольник, у кот все стороны равны); 2) генетические. Указывает на происхождение понятий(сфера, окружность…); 3) аксиоматический сп-б-определение понятия ч/з с-му аксиом; 4) индуктивный сп-б. Это сп-б получения все элементов понятия арифм и геометр прогрессии; 5) контекстуальныеопределения. Опред-е понятия ч/з текст; 6) Остенсивные определения- определение понятия ч/з демонстрацию.

Осн требования к опред понятий: 1) определяемое и определяющее понятие должны быть соразмерным (их объемы должен совпадать); 2) в определении понятия должны быть указаны св-ва, кот позволяют выделить данный объект среди мн-ва др объектов; 3) отсутствие в отрицании избыточности; 4) запрещается порочный круг. Нельзя определить понятие ч/з само себя или понятие определить ч/з другое ч/з первое; 5) определяемый объект должен существовать.