Деление на двузначное и трехзначное число

ДЕЛЕНИЕ НА ДВУЗНАЧНОЕ И ТРЕХЗНАЧНОЕ ЧИСЛО

В основе устного деления на двузначное и трехзначное число лежит свойство деления числа на произведение:а : (b • с) = (а : b) : с

ПРИЕМЫ ЗАПОМИНАНИЯ ТАБЛИЦЫ УМНОЖЕНИЯ

1. Прием счета двойками, тройками, пятерками;

2. Прием последовательного сложения( данный прием связан со смыслом действия умножения как сложения одинаковых слагаемых);

3. Прием прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата)

4. Прием взаимосвязанной пары: 2 • 6 6 • 2 (перестановка множителей)

5. Прием запоминания последовательности случаев с ориентиром на возрастание второго множителя

6. Прием «порции» (активно реализован в учебнике математики для 2 и 3 классов автора Н.Б. Истоминой. Для заучивания ребенку предлагается «порция», состоящая из 2—3 случаев, но не по принципу возрастания второго множителя.Например, «порция» состоит из трех случаев: 9 • 5; 9 • 6; 9 • 7. Первым для заучивания предлагается случай 9 • 6, а от него, используя прием 3, ребенок переходит к случаям 9 • 5 и 9 • 7.В следующий раз «порция» снова содержит три случая 9 • 4; 9 • 3; 9 • 2. Здесь опорным случаем является случай 9 • 3.)

7. Прием запоминающегося случая в качестве опорного (используются легко запоминающиеся случаи: 7 • 7, 5 • 5 и т. п. Применяя затем прием прибавления или вычитания первого множителя, ребенок получает нужные результаты)

8. Прием внешней опоры (в качестве опоры используется рисунок или прямоугольная таблица чисел)

9. Прием запоминания таблицы «с конца» (прием активно реализован в учебнике Н.Б. Истоминой. Он рекомендуется для использования при работе с детьми, плохо запоминающими большие объемы информации. В этом случае установка на запоминание ребенку дается порциями, начиная с самых сложных случав: 9 • 9,9 • 8,9 • 7. Таким образом, ребенок с ограниченным объемом запоминания запомнит сначала самые сложные случаи, а более легкие случаи таблицы чисел 2,3 и 4 он может получать приемом сложения одинаковых слагаемых или любым другим приемом)

10. Пальцевый счет при запоминании таблицы умножения

11. Мнемонические приемы при заучивании таблицы умножения(это могут быть карточки с записями табличных случаев, которые ребенок носит в кармане и просматривает при любом удобном случае (в транспорте, в очереди и т. п.).

Табличное деление

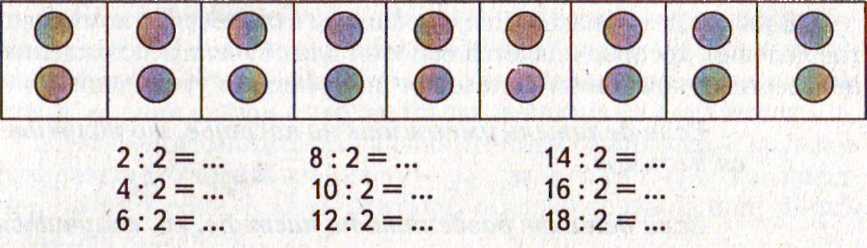В начальной школе действие деления рассматривают как действие обратное умножению. В связи с этим сначала дети знакомятся со случаями деления без остатка в пределах 100 — так называемым табличным делением. С действием деления дети знакомятся после того, как уже выучили наизусть таблицы умножения чисел 2 и 3. На основе знания этих таблиц уже на четвертом уроке после зна­комства с делением, составляется первая таблица деления на 2. Для получения ее значений используют предметный рисунок.

Значения частных в этой таблице получают подсчетом элементов рисунка на картинке.

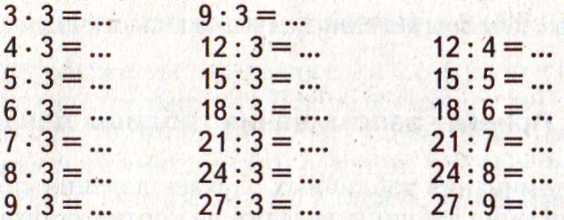Следующая таблица деления — деление на 3 является последней таблицей, изучаемой во втором классе. Составляется эта таблица на основе взаимосвязи компонентов умножения с использованием правила нахождения неизвестного множителя. В связи с тем, что данное правило в явном виде предлагается детям в полной формулировке только в 3 классе, на этапе составления таблицы деления на 3 по-прежнему целесообразнее опираться на предметную модель действия (модель на фланелеграфе или рисунок).

Например: Вычисли и запомни результаты действий.

Для проверки используй рисунок:

Использование такого рисунка дает возможность составить и третий, взаимосвязанный с первыми двумя, случай деления (третий столбик). Он не относится к таблице деления на 3, но является членом взаимосвязанной тройки, который легче запоминать, ориентируясь на первые два случая. Такой прием запоминания таблицы деления (ориентир на взаимосвязанную тройку) является удобным мнемоническим приемом. Можно видеть, как дети пользуются им, реально запоминая только один прием действия умножения.

Все остальные таблицы деления изучаются в 3 классе. Поскольку умножение числа 4 и умножение на 4 также изучается уже в 3 классе, на этом году обучения прекращается практика раздельного изучения таблиц умножения и деления. Начиная с таблицы умножения числа 4, взаимосвязанные с ней таблицы деления изучают на одном уроке, сразу составляя четыре взаимосвязанных столбика случаев умножения и деления.

Например:

Используя результаты первого столбика, дети получают второй столбик перестановкой множителей, а результаты третьего и четвертого столбиков — на основе правила взаимосвязи компонентов умножения:

Деление с остатком.

Деление с остатком изучается во II классе после завершения работы над внетабличными случаями умножения и деления.

Работа над делением с остатком в пределах 100 расширяет знания учащихся о действии деления, создает новые условия для применения знаний табличных результатов умножения и деления, для применения вычислительных приемов внетабличного умножения и деления, а также своевременно готовит учащихся к изучению письменных приемов деления.

Особенностью деления с остатком по сравнению с известными детям действиями является тот факт, что здесь по двум данным числам — делимому и делителю — находят два числа: частное и остаток.

Дети в своем опыте неоднократно встречались со случаями деления с остатком, выполняя деление предметов (конфет, яблок, орехов и т. д.). Поэтому при изучении деления с остатком важно опираться на этот опыт детей и вместе с тем обогатить его. Полезно начать работу с решения жизненно практических задач. Например: «15 тетрадей раздай ученикам, по 2 тетради каждому. Сколько учеников получили тетради и сколько тетрадей осталось?»

Ученики раздают, раскладывают предметы и устно отвечают на поставленные вопросы.

Наряду с этими заданиями проводится работа с дидактическим материалом и с рисунками.

Делим 14 кружков по 3 кружка. Сколько раз по 3 кружка содержится в 14 кружках? (4 раза.) Сколько кружков остается? (2.) Вводится запись деления с остатком: 14:3=4 (ост. 2). Ученики решают несколько аналогичных примеров и задач, используя предметы или рисунки. Возьмем задачу:" «Мама принесла 11 яблок и раздала их детям, по 2 яблока каждому. Сколько детей получили эти яблоки и сколько яблок осталось?» Ученики решают задачу с помощью кружков .

Решение и ответ задачи записываются следующим образом-11:2=5 (ост. 1).

Ответ: 5 детей и остается 1 яблоко.

Затем раскрывается соотношение между делителем и остатком, т. е. ученики устанавливают: если при делении получается остаток, то он всегда меньше делителя. Для этого сначала решаются примеры на деление последовательных чисел на 2, затем на 3 (4, 5). Например:

10:2=5 12:3 = 4 16:4 = 4
11:2=5(ост.1) 13:3 = 4 (ост. 1) 17:4 = 4(ост 1)
12:2=6 14:3 = 4(ост. 2) 18:4 = 4 (ост. 2)

13:2=6(ост.1) 15:3 = 5 19:4 = 4 (ост. 3)

Учащиеся сравнивают остаток с делителем и замечают, что при делении на 2 в остатке получается только число 1 и не может быть 2 (3, 4 и т. д.). Точно так же выясняется, что при делении на 3 остатком может быть число 1 или 2, при делении на 4 — только числа 1, 2, 3 и т. д. Сравнив остаток и делитель, дети делают вывод, что остаток всегда меньше делителя.

Чтобы соотношение это было усвоено, целесообразно предлагать упражнения, аналогичные следующим:

Какие числа могут получиться в остатке при делении на 5, 7, 10? Сколько различных остатков может быть при делении на 8, 11, 14? Какой наибольший остаток может быть получен при делении на 9, 15, 18? Может ли при делении на 7 получиться в остатке 8, 3, 10?

Для подготовки учащихся к усвоению приема деления с остатком полезно предлагать следующие задания:

Какие числа от 6 до 60 делятся без остатка на б, 7, 9? Какое ближайшее к 47 (52, 61) меньшее число делится без остатка на 8, 9, 6?

Раскрывая общий прием деления с остатком, лучше брать примеры парами: один из них на деление без остатка, а другой 'на деление с остатком, но примеры должны иметь одинаковые делители и частные.

Далее решаются примеры на деление с остатком без примера-помощника. -Пусть надо 37 разделить на 8. Ученик должен усвоить следующее рассуждение: «37 на 8 без остатка не делится. Самое большое число, которое меньше, чем 37, и делится на 8 без остатка, 32. 32 разделить на 8, получится 4; из 37 вычтем 32, получится 5, в остатке 5. Значит, 37 разделить на 8, получится 4 и в остатке 5».

Навык деления с остатком вырабатывается в результате тренировки, поэтому надо больше включать примеров на деление с остатком как в устные упражнения, так и в письменные работы.

Выполняя деление с остатком, учащиеся иногда получают остаток больше делителя, например: 47:5=8 (ост. 7). Чтобы предупредить такие ошибки, полезно предлагать детям неверно решенные примеры, пусть они найдут ошибку, объяснят причину ее появления и решат пример правильно.

ПАМЯТКА

1. подбери число, близкое к делимому, которое меньше его и делится без остатка;

2. раздели это число;

3. найди остаток;

4. проверь остаток, меньше ли делителя;

5. запиши пример

Во II и III классах надо как можно больше включать разнообразных упражнений на все изученные случаи умножения и деления: примеры в одно и несколько действий, сравнение выражений, заполнение таблиц, решение уравнений и т.д.

№ 14. Понятие составная задача.

Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к разбиению ее на ряд простых задач и последовательному их решению. Таким образом, для решения составной задачи надо установить ряд связей между данными и искомым, в соответствии с которыми выбрать, а затем выполнить арифметические действия.

В решении составной задачи появилось существенно новое сравнительно с решением простой задачи: здесь устанавливается не одна связь, а несколько, в соответствии с которыми выбираются арифметические действия. Поэтому проводится специальная работа по ознакомлению детей с составной задачей, а также по формированию у них умений решать составные задачи.

Подготовительная работа к ознакомлению с составными задачами должна помочь учащимся уяснить основное отличие составной задачи от простой —ее нельзя решить сразу, т. е. одним действием, а для решения надо вычленить простые задачи, установив соответствующие связи между данными и искомым. С этой целью предусматриваются специальные Упражнения:

Выполни решение.

Этапы. решения задач

На первом этапе дети должны усвоить суть каждого отдельного задания и научиться выполнять их. Например, понимать, что значит «представить себе то, о чем говорится в задаче»; что значит «составить план решения» и т. д., а также уметь представить себе то, о чем говорится в задаче, уметь составить план решения и т. д.

Этот этап овладения отдельными умениями проходит в I классе, когда учитель каждый раз при решении задачи сам называет задания и учит их выполнять.

На втором этапе (II класс, начало учебного года)' учащиеся знакомятся с системой заданий и учатся ими пользоваться при решении задач.

Учащиеся получают карточки, на которых записаны задания. При работе над каждой задачей, примерно в течение 6—10 уроков, каждое задание читается одним из детей вслух и при их выполнении рассуждение тоже ведется вслух.

На третьем этапе учащиеся должны усвоить систему заданий и самостоятельно пользоваться ими при решении задач. С этой целью на последующих 10—15 уроках при решении задач учащиеся продолжают пользоваться карточками с заданиями, но задания читают про себя, а рассуждение ведут вслух. В результате такой работы учащиеся непроизвольно овладевают системой заданий.

На четвертом этапе у учащихся вырабатывается умение работать над задачей в соответствии с заданиями. На этом этапе карточки не нужны детям, так как вся система заданий усвоена ими в такой мере, что учащиеся руководствуются ими, ведя рассуждение про себя и очень быстро.

Формируя общий метод paботы над задачей, учитель должен иметь в виду, что не все дети одновременно овладевают этим методом: если одним детям достаточно месяца работы по карточкам, то другим надо два-три месяца. Поэтому не следует запрещать пользоваться карточками тем учащимся, которые еще не овладели общим методом. Но ни в коем случае нельзя специально разучивать эти задания — они должны быть усвоены непроизвольно в результате многократного их выполнения.

Работая над задачей отдельного вида, надо по-разному подходить к использованию заданий: на ступени ознакомления с задачей нового вида чаще выполняют все задания, а на ступени обобщения способа решения этого делать не требуется, иначе выполнение заданий превратится в самоцель и будет тормозить обобщение способа решения. На этой ступени, когда формируется умение решать задачи какого-либо вида, учащиеся должны выполнять задания по порядку до тех пор, пока не найдут способ решения. Так, если после чтения задачи ученик уже знает, как ее решить, то пусть решает, а если не знает, пусть выполнит следующее задание, «позовет следующего помощника»: запишет задачу кратко и попробует ее решить и т. д. В крайнем случае, если, выполнив все задания, ученик все же не найдет решения, на помощь приходит сам учитель.

№ 28Нумерация чисел в пределах 100

В результате изучения темы должно быть обеспечено:

1. Закрепление знания чисел в пределах 20 и порядка их следование при счете. Умение воспроизводить последовательность чисел от 1 до 20 в «прямом и обратном направлениях», начиная с любого заданного числа. Умение считать предметы в пределах 20, устанавливать порядковый номер предмета при счете.

2. Овладение умением сравнивать числа по месту, которое они занимают в ряду (пределах 20).

3. Сознательное овладение умением считать и записывать числа в пределах 20; умение представлять двузначное число в виде суммы десятка и единиц.

Задача учителя при изучении этой темы — научить детей считать до 100, показать, как образуются числа из десятков и единиц, научить читать и записывать двузначные числа на основе твердого знания о том, что единицы пишутся на первом, а десятки — на втором месте, считая справа налево. Необхо­димо также добиться усвоения учащимися новых понятий и тер­минов: единицы первого и второго разряда, разрядное число, сумма разрядных слагаемых, однозначное и двузначное число.

В изучении нумерации выделяются две ступени:

– сначала изучается нумерация чисел 11—20

– затем чисел 21 —100.

Такой порядок изучения обусловлен тем, что названия чисел второго десятка образуются из тех же слов, что и названия разрядных чисел (20, 30, ..., 90). Однако слова «два», «три», «пять» и т. д. в числительных две-на-дцать, три-на-дцать и т. д. обозначают число единиц, а в числительных два-дцать, три-дцать и т. д. обозначают число десятков (за исключением слов «сорок» и «девяносто»). Кроме того, при написании только чисел второго десятка порядок называния составляющих их разрядных чисел и порядок записи не совпадают: сначала называются единицы (три-на-дцать), а пишется первым десяток (13), в то время как во всех остальных случаях чтение и запись разрядных чисел совпадают (23, 145, 1972 и т. п.). Эти особенности нумерации требуют того, чтобы числа второго десятка были рассмотрены отдельно. Но вместе с тем нумерация двузначных чисел до 20 и свыше 20 принципиально сходна: устная и письменная нуме­рация этих чисел опирается на десятичную группировку единиц при счете и на принцип поместного значения цифр при записи чисел, поэтому нумерация чисел от 10 до 20 и от 20 до 100 изучается в одном концентре.

Подготовительная работа к изучению нумерации чисел вто­рого десятка проводится при повторении материала по теме «Десяток». С этой целью включаются упражнения в счете пред­метов с выходом за десяток (например, сколько учеников в первом ряду, во втором ряду? Сколько всего учеников в классе? И т. п.), а также упражнения в счете групп предметов (напри­мер, сколько пар детей стоит у доски? Сколько на картинке пар лыж, пар обуви?).

Изучение устной нумерации чисел второго десятка начинается с формирования у детей понятия о десятке. От­считывая по 10 палочек и завязывая их в пучки, учащиеся узна­ют, что десять единиц образуют десяток. Затем, выполняя упражнения в счете десятков палочек, сложении и вычитании десятков с использованием палочек, дети убеждаются, что де­сятки можно считать, складывать и вычитать как простые еди­ницы (см. урок на стр. 37—38).

Далее рассматривается образование чисел от 11 до 20 из десятков и единиц и поясняются их названия.

Так же рассматривается образование и название других чи­сел второго десятка и одновременно порядок их следования при счете.

Помимо палочек, в качестве наглядного пособия используют полоски, на каждой из которых по 10 кружков (десятки), и по­лоски с 1, 2, 3, . . . ,9 кружками (единицы).

Для закрепления знаний десятичного состава и натурального следования чисел в пределах 20 предлагают учащимся — сна­чала с опорой на наглядные пособия, а потом без них — такие упражнения: «Отсчитайте 15 палочек; узнайте, сколько это со­ставляет десятков палочек и сколько отдельных палочек; возь­мите 1 десяток палочек и еще 4 палочки. Сколько всего палочек взяли?

Далее учащиеся знакомятся со второй единицей длины — дециметром как десятком сантиметров. Включаются упражне­ния в черчении и измерении отрезков, длина которых выража­ется как простыми именованными числами (12 см), так и составными (1 дм 5 см). Опираясь на сравнение отрезков, дети учатся сравнивать числа, полученные при измерении, и постепенно овладевают умениями заменять крупные единицы мелкими (1 дм 3 см = 13 см) и обратно (20 см — 2 дм). При этом закрепляются знания десятичного состава. Например, 1 дм 3 см надо выразить в сантиметрах. Ученик рассуждает так: 1 дм — это 1 десяток сантиметров; 1 десяток и 3 см составляют.

На следующем этапе приступают к изучению письмен­ной нумерации. Чтобы раскрыть поместный принцип записи двузначных чисел, используют абак -- таблицу с двумя рядами карманов: один ряд —для палочек, другой —для раз­резных цифр. Знакомя с пособием, учитель показы­вает, как ставят в верхних карманах палочки, когда их 5, 9, 10, 14 штук. Затем ученикам пред­лагают разложить в карманы, на­пример, 15, 17 палочек.

Учитель. Сколько здесь всего палочек?

Ученик. Семнадцать.

Учитель. Сколько десятков?

Ученик. Один.

Учитель. Обозначим это цифрой (вставляет в левый ниж­ний карман цифру 1). Сколько единиц в числе 17? Обозначим это цифрой (вставляет в правый • нижний карман цифру 7). У нас записано число 17. Что обознача­ет цифра 7, которая стоит на пер­вом месте справа?

Ученик. Семь единиц.

Учитель. Что обозначает цифра 1, которая стоит на вто­ром месте?

Ученик. Один десяток.

Аналогично рассматривают еще несколько чисел, а затем дети записывают числа в своих тетрадях в таблицах с надпи­сями «десятки» и «единицы» и объясняют значение каждой цифры.

Особо рассматривается запись чисел 10 и 20: цифра 1 (2) показывает, что в числе содержится 1 десяток (2 десятка), циф­ра 0 — в числе отсутствуют единицы.

Упражняясь в записи чисел, учащиеся закрепляют знания десятичного состава и натурального следования чисел в пре­делах 20. Например, учитель предлагает записать число, кото­рое состоит из 1 десятка и 9 единиц.

Опираясь на наглядные пособия, учащиеся знакомятся со случаями сложения и вычитания вида: 10 + 5, 15 — 5, 15—10. Выполняя такие вычисления, учащиеся закрепляют знания деся­тичного состава чисел: например, 10+5, десять — это 1 деся­ток, 1 десяток и 5 единиц составляют число 15.

Сопоставляя числа, учащиеся устанавливают, что для записи числа, состоящего из единиц, требуется одна цифра (один знак); для записи числа, состоящего из десятков или десятков и еди­ниц, требуется две цифры (два знака). Вводятся термины «одно­значные» и «двузначные» числа. Дети приводят примеры одно­значных и двузначных чисел, выполняют упражнения на разли­чение однозначных и двузначных чисел, например: «Выпишите из ряда чисел сначала однозначные, а потом двузначные числа: 2, 13, 8, 17, 15, 6, 11, 10; запишите 4 любых однозначных числа и увеличьте каждые на 10. Какие числа у вас получились, как можно их. назвать?

Изучение нумерации чисел в пределах 100 идет в таком же плане, как и в пределах 20: сначала изучается устная, затем письменная нумерация.

Опираясь на сформированное понятие новой счетной (раз­рядной) единицы — десятка, рассматривают образование и на­звание разрядных чисел 20, 30 и т. д., а затем образование любых (неразрядных) чисел на основе счета десятков и единиц (4 дес. 5 ед. — это 45 и т. п.).

Усвоению десятичного состава чисел способствуют упраж­нения в образовании и разложении чисел. (Какое число состав­ляют 5 дес. 7 ед.?) С этой же целью рассматривается сложение и вычитание вида: 70 + 5, 8 + 20, 34 — 4, 48 — 40. Приемы вычислений здесь те же самые, что и для аналогичных случаев в пределах 20, и мето­дика работы сходна.

Как и при изучении нумерации чисел второго десятка одно­временно с нумерацией отвлеченных чисел рассматривается нумерация именованных чисел (запись, замена крупных единиц мелкими и мелких крупными, сравнение чисел). Одновременно с десятичным составом рассматривается нату­ральное следование чисел первой сотни. Для этого включаются упражнения в счете предметов, в присчитывании по одному и по десять с опорой на наглядное пособие — «ленту ста». Приме­няются знания о натуральной последовательности чисел при выполнении таких упражнений: «Перед каким числом называют при счете число 79? После какого числа при счете называют число 100? Решите примеры: 89 + 1, 70— 1».

При изучении письменной нумерации чисел в пределах 100 опираются на умение учащихся записывать числа второго де­сятка, а также на знания десятичного состава чисел первой сотни. Сначала числа иллюстрируют палочками и пучками па­лочек на абаке, после чего обозначают число единиц и число десятков разрезными цифрами. Рассмотрев, таким образом, не­сколько чисел (например, 16, 26, 66, 60 и др.), учащиеся делают вывод о том, что в двузначном числе единицы пишутся на пер­вом месте, а десятки — на втором, считая справа налево. Усваи­вается этот вывод в процессе выполнения таких упражнений: «Объясните, что обозначает каждая цифра в записи чисел (77, 25, т. п.), запишите с по­мощью данных цифр (например, 5,7, 1) всевозможные двузначные числа (при записи отдельных чисел можно использовать одну и ту же цифру дважды)».

При изучении письменной ну­мерации учащиеся знакомятся с разрядом и разрядным числом. Учитель поясняет, что, например, в числе 57 содержится 5 десятков и 7 единиц или иначе можно сказать: 5 единиц второго разряда и 7 единиц первого разряда. Полезно при этом использовать наглядное пособие — карточки с разрядными числами, которые имеются в приложении к учебнику математики I класса. Прак­тические действия с карточками помогают детям овладеть уме­нием представлять число в виде суммы разрядных слагаемых (48 = 40 + 8 и т. п.), что необходимо для выполнения действий над двузначными числами.

С целью систематизации знаний по нумерации полезно в конце работы над темой включать задания по характеристике заданных чисел. Характеризуя, например, число 33, учащиеся могут назвать его десятичный состав (в этом числе 3 дес. и 3 ед., или 3 ед. II разряда и 3 ед. I разряда), сказать о месте этого числа в натуральной последовательности (число 33 назы­вают при счете после 32 и перед 34), об особенностях записи этого числа (это число двузначное, для его записи использована 2 раза цифра 3) и др.

Усвоение нумерации требует длительных упражнений, поэто­му в дальнейшем, при изучении сложения и вычитания в преде­лах 100, систематически включают в устные упражнения зада­ния по устной и письменной нумерации чисел.

№ 12методика решения задач на пропорциональное деление

Основным признаком задач на пропорциональное деление является содержащееся в задаче требование распределить одно численное значение величины (например, стоимости) соответственно данным числам (например, соответственно числу вещей в одной группе и числу вещей в другой группе). Решаемые в начальных классах задачи на пропорциональное деление можно представить в виде таблицы. Эти задачи включают две переменные величины, связанные пропорциональной зависимостью, и одну или больше постоянных, причем даны два или более значений одной переменной и сумма соответствующих значений другой переменной: слагаемые этой суммы являются искомыми. Применительно к каждой группе величин, связанных пропорциональной зависимостью, можно выделить 6 видов задач на пропорциональное деление, четыре из которых с прямо пропорциональной зависимостью величин, а две с обратно пропорциональной зависимостью.

классификация задач на пропорциональное деление с прямо пропорциональной зависимостью величин представлены в таблице:

№ задач	Величины	Задачи
Цена	Количество	стоимость
I.	Постоянная	Даны два или более значений	Дана сумма значений, соответствующих количеству. Найти слагаемые	Ученица купила по одинаковой цене 6 тетрадей в клетку и 4 тетради в линейку. Всего она уплатила 20 коп. Сколько стоили тетради в клетку и в линейку в отдельности?
II.	постоянная	Дана сумма значений, соответствующих стоимости. Найти слагаемые	Даны два или более значений	Ученица купила по одинаковой цене тетради в клетку и линейку, всего 10 штук. За тетради в клетку она уплатила 12 коп., а за тетради в линейку 8 коп. Сколько было куплено тетрадей в клетку и в линейку в отдельности?
III.	Даны два или более значений	Постоянное	Дана сумма значений, соответствующих цене. Найти слагаемые	В магазине продали одинаковое количество шапок и шарфов. Шапка стоила 5 руб., а шарф 3 руб. За все проданные вещи выручили 160 руб. Сколько стоили все шапки и шарфы в отдельности?
IV.	Дана сумма значений, соответствующих стоимости. Найти слагаемые	Постоянное	Даны два или более значений	В магазине продали одинаковое количество шапок и шарфов. Шапка с шарфом стоили 8 руб. За все шапки выручили 100 руб., а за все шарфы 60 руб. Сколько стоили шапка и шарф в отдельности?

2. Методика решения задач на пропорциональное деление.

В начальных классах задачи на пропорциональное деление решаются только способом нахождения значения постоянной величины.

Подготовкой к решению задач на пропорциональное деление надо считать твердое умение решать задачи на нахождение четвертого пропорционального.

При ознакомлении с задачами на пропорциональное деление лучше предлагать их не в готовом виде, а составить вместе с детьми из задач на нахождение четвертого пропорционального. Это поможет увидеть связи между задачами этих видов, что быстрее приведет учащихся к обобщению способа их решения.

Учащимся предлагается составить задачу по ее краткой записи:

Цена	Количество	Стоимость
Одинаковая	6тетрадей 4 тетради	12 коп. ?

После решения задачи, составленной по данному условию, учитель записывает вместо вопросительного знака число, полученное в ответе (8 коп.). Затем он предлагает найти сумму чисел, которые показывают стоимость тетрадей (20 коп.), и составить задачу по новому условию:

Цена	Количество	Стоимость
Одинаковая	6 тетрадей 4 тетради	? ? 20 коп.

Дети составляют задачу на пропорциональное деление, ставя два вопроса: «Сколько уплатил первый покупатель?» и «Сколько уплатил второй покупатель?» Учитель поясняет, что эти два вопроса можно заменить одним: «Сколько денег уплатил каждый покупатель?» В окончательном виде задача формулируется примерно так: «Два мальчика купили тетради по одинаковой цене. Первый купил 6 тетрадей, а второй — 4. Всего они уплатили 20 коп. Сколько денег уплатил каждый мальчик?»

Что требуется узнать в задаче? Что значит «каждый»? Можно ли сразу узнать, сколько уплатил первый мальчик? Почему нельзя? Можно ли сразу узнать цену тетради? Почему нельзя? Можно ли сразу узнать, сколько купили тетрадей на 20 коп.? Почему можно? Что узнаем первым действием; вторым; третьим; четвертым?

Решение задачи записывается в форме отдельных действий с пояснениями.

Далее включается решение готовых задач. В этом случае вопрос задачи разбивают на два вопроса; затем выяснить, которое из искомых чисел должно быть больше и почему; далее переходят к составлению плана решения, ведя рассуждение от вопроса к числовым данным. Проверка решения выполняется способом установления соответствия между числами, полученными в ответе, и данными: надо сложить числа, полученные в ответе, и должно получиться число, данное в задаче.

Пример ознакомления с задачами на пропорциональное деление

Подготовкой к решению задач данного вида является умение решать задачи на нахождение четвертого пропорционального. Для ознакомления с задачами на пропорциональное деление в учебнике предлагается одновременно две задачи

1) Детям купили игрушки: Оле 6 одинаковых стульев, а Кате 4 таких же стула. Все стулья стоили 500 р. Сколько стоит 1 стул?

2) Детям купили: Оле 6 одинаковых стульев, а Кате 4 таких же стула. Все стулья стоили 500 р. Сколько стоят 6 стульев, купленных Оле, и сколько стоят 4 стула, купленных Кате?

Первая задача является подготовительной ко второй задаче. Ученики читают задачу и рассматривают рисунок в учебнике. После этого записывают задачу кратко под руководством учителя и решают устно.

Какие величины даны в задаче? (Цена, количество, стоимость.) Запишем. Что известно? (Количество стульев: Оле купили 6 одинаковых стульев, а Кате - 4 таких же стула; известна стоимость - все стулья стоили 500 р.) Что надо узнать? (Цену.) Что известно о цене? (Она одинаковая.) Запишем. Получается запись.

Можно ли сразу узнать цену стула? (Нет.) Почему? (Не знаем, сколько всего стульев купили.) А это можно узнать? (Можно.) Как решим эту задачу? (Сначала узнаем, сколько стульев купили: к 6 прибавим 4, получится 10. Купили 10 стульев. Теперь узнаем цену стула: разделим 500 на 10, получится 50. Цена стула - 50 р.)

Прочитайте задачу (2) и скажите, чем она отличается от предыдущей. (Эта задача отличается вопросом: здесь надо узнать не цену стула, а стоимость 6 стульев и 4 стульев.) Запишем в краткой записи два вопросительных знака:

Цена	Количество	Стоимость
Одинаковая - ?	6 стульев   4 стула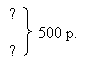

Здесь два вопроса задачи. Назовите их. (Сколько стоят 6 стульев и сколько стоят 4 стула.) Как узнать, сколько стоят 6 стульев? (Надо цену стула умножить на 6, а как находить цену, мы уже знаем.) Как же решить задачу? (Сначала узнаем, сколько купили всего стульев, затем цену стула, потом стоимость 6 стульев.) Нельзя ли теперь узнать стоимость 4 стульев? (Можно: цену стула умножить на 4.)

Эту первую задачу на пропорциональное деление полезно решить с записью отдельных действий и пояснений к ним или так называемых вопросов:

1) Сколько всего стульев купили?

6+4=10 (ст.)

2) Сколько стоит один стул?

500:10=50 (р.)

3) Сколько стоят 6 стульев?

50·6=300 (р.)

4) Сколько стоят 4 стула?

50·4=200 (р.)

Проверка: 300+200=500 (р.)

Ответ: 6 стульев стоят 300 р., 4 стула - 200 р.

При первоначальном ознакомлении применять чертеж нецелесообразно, т.к. учащиеся усваивают формальные рассуждения: "считаем маленькие отрезки, (их 10), потом 500:10=5 и 5 6=30, 5 4=20", т.е. происходит преждевременное сокращение рассуждений. Разбор задачи изображать в виде графической схемы тоже нецелесообразно, т.к. она начнется с двух вопросов и вызывает затруднение учащихся.

№ 17 Методика решения задач на нахождение четвертого пропорционального

В начальных классах рассматривается решение задач, связанных с пропорциональными величинами: задачи на нахождение четвертого пропорционального (на простое тройное правило), на пропорциональное деление и на нахождение неизвестных по двум разностям, задачи, связанные с движением.

В задачах на нахождение четвертого пропорционального даются три величины, связанные с пропорциональной зависимостью (прямой, обратной) и, исходя из которых, находят четвертую, искомую величину. Эти четыре величины составляют пропорцию, отсюда и название этих задач.

Величинами в этих задачах могут быть цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и другие.

Решение этих задач основывается на знании связей между величинами (зная цену товара и его количество, можно найти стоимость, выполнив действие умножения).

Перестановка слагаемых

Правило перестановки слагаемых: От перестановки слагаемых сумма не изменяется.

Свойство перестановки слагаемых (переместительное свойство сложения) используется в 1 классе при знакомстве с вычислительными приемами вида а + 5, а+ 6, а+ 7, а + 8 и а + 9.

№7 Вычислительные приемы для многозначных чисел

Способы устных вычислений

Устные приемы сложения и вычитания многозначных чисел изучаются в 4 классе четырехлетней начальной школы в следую­щем порядке:

Нумерационные случаи

а) Случаи вида:

99 999 + 1 345 ООО - 1 560 999 + 1

560 ООО - 1 399 999 + 1 40 ООО - 1

При выполнении вычислений данного вида ссылаются на принцип построения натурального ряда чисел: добавление к числу единицы дает число, следующее по счету; вычитание единицы дает число, предшествующее по счету.

Например: 399 999 + 1 — добавляя к числу 1, получаем число следующее. Следующее за числом 399 999 число 400 000, значит 399 999 + 1 = 400 000.

б) Случаи вида:

30 000 + 1 000 650 999 - 900 600 000 + 5

60 345 - 5 345 000 - 45 000 800 700 + 1 000

При выполнении вычислений данного вида ребенок должен хорошо знать принцип поразрядного строения чисел в десятичной системе счисления.

Смысл действия деления

Действие деления рассматривается в начальной школе как действие, обратное умножению.

С теоретико-множественной точки зрения смыслу деления соответствует операция разбиения множества на равночисленные подмножества. Таким образом, процесс нахождения результатов действия деления связан с предметными действиями двух видов:

а) разбиение множества на равные части (например, 8 кружков разложили в 4 коробки поровну — раскладывают 8 кружков по одному в 4 коробки, а затем считают, сколько кружков получилось в каждой коробке);

б) разбиение множества на части по сколько-то в каждой части (например, 8 кружков разложили в коробки по 4 штуки — раскладывают 8 кружков по 4 штуки в коробки, а затем считают, сколько получилось коробок; деление по этому принципу в методике называют «деление по содержанию»).

Используя подобные предметные действия и рисунки, дети находят результаты деления.

Выражение вида 12:6 называют частным. Число 12 в этой записи называют делимым, а число 6 — делителем. Запись вида 12 : 6 = 2 называют равенством. Число 2 называют значением выражения. Поскольку число 2 в данном случае получено в результате деления, его также часто называют частным.

Задания, требующие распознавания компонентов действий и употребления их названий в речи.

1. Среди данных выражений найдите такие, в которых делитель равен 3:

2:2 6:3 6:2 10:5 3:1 3-2 15:3 3-4

2. Составьте частное, в котором делимое равно 15. Найдите его зна