Методы расчета сводных характеристик выборки
Литература. Гмурман. Ч. 3. Гл.18, 19, §§ 8,9.
Пример 1.Исследовать статистически случайную величину X – прочность (разрывная нагрузка), мН, пряжи линейной плотности 18,5 текс. Для этого получена выборка объема n = 40. Результаты испытаний приведены в таблице
144, 149, 199, 174, 176, 183, 239, 208,
120, 150, 203, 160, 180, 207, 221, 220,
117, 158, 170, 282, 177, 218, 210, 190,
225, 149, 250, 101, 179, 236, 198, 193,
230, 240, 163, 238, 178, 183, 213, 211.
Так как объём статистической совокупности n ³ 40, то все множество значений выборки разбивается на классы. Число классов k определяется по объему выборки n с помощью таблицы.
| Объём выборки n | 40 – 60 | 60 – 100 | 100 – 200 | 200 – 500 |
| Число классов k | 6 – 7 | 7 – 10 | 10 – 14 | 14 – 17 |
Выбираем k =6.
Найдем длину классового промежутка D по формуле
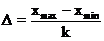 . (1)
. (1)
Здесь xmax наибольшее и xmin наименьшее значения.По таблице находим xmin = 101; xmax = 282. Тогда длина классового промежутка
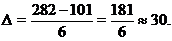
Значение D берется приближенно с той же точностью, с которой определены значения элементов выборки. Определяем границы классовых промежутков.
Левая граница первого промежутка принимается равной 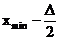 . Левая граница каждого следующего промежутка получается прибавлением D к левой границе предыдущего промежутка. Правый конец каждого промежутка меньше левого конца следующего промежутка на единицу последнего десятичного разряда значений в таблице исходных данных. Этим обеспечивается то, что каждое значение выборки попадает только в один интервал.
. Левая граница каждого следующего промежутка получается прибавлением D к левой границе предыдущего промежутка. Правый конец каждого промежутка меньше левого конца следующего промежутка на единицу последнего десятичного разряда значений в таблице исходных данных. Этим обеспечивается то, что каждое значение выборки попадает только в один интервал.
Все элементы выборки должны относиться к тому или иному классовому промежутку. При этом все элементы, попавшие в один и тот же промежуток, считаются равными между собой и равными среднему арифметическому границ промежутка. Отметим, что достаточно найти середину только одного из классовых промежутков, так как середины соседних промежутков отличаются друг от друга на D. Теперь вместо исходной выборки изучается ее приближение, выборочный ряд середин промежутков 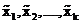 .
.
Создаем расчетную таблицу
| Границы промежутков. от и до | Середины проме-жутков 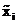 | Штрихо- вание | Частоты Z | Условные значения a | aZ | a2 Z | a3 Z | a4 Z |
| ## ## // |  | |||||||
| Сумма |
Левая граница 1-го интервала 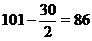 . Далее 86 + 30 = 116; 116 + 30 = 140 и т. д. Правая граница первого интервала 116 - 1=115, следующая – 115 + 30 = 145 и т.д. Затем заполняем второй столбец
. Далее 86 + 30 = 116; 116 + 30 = 140 и т. д. Правая граница первого интервала 116 - 1=115, следующая – 115 + 30 = 145 и т.д. Затем заполняем второй столбец 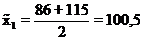 ,
, 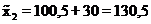 и т.д. Всего получится k + 1промежуток, в нашем случае 6+1=7. xmax лежит внутри последнего промежутка.
и т.д. Всего получится k + 1промежуток, в нашем случае 6+1=7. xmax лежит внутри последнего промежутка.
Таблица 1.
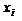 | 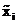 | 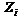 | ai | aiZi | 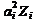 | 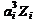 | 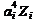 | |
| 86 – 115 116 – 145 146 – 175 176 – 205 206 – 235 236 – 265 266 – 295 | 100,5 130,5 160,5 190,5 220,5 250,5 280,5 | / /// ## /// ## ## // ## ## ## / | -3 -2 -1 | -3 -6 -8 | -27 -24 -8 | |||
| Сумма |
После того как заполнены столбцы 1 и 2 , переходим к столбцу 3. Для каждого элемента выборки находят классовый промежуток, которому принадлежит этот элемент, и в строке этого промежутка в столб. 3 ставят штрих. Рекомендуется четыре штриха ставить вертикально, а пятый – горизонтально, перечеркивая им четыре предыдущих. Сумма штрихов в ячейке равна частоте соответствующего значения и записывается рядом (в столб. 4). Частоты обозначаются 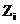 и их сумма ставится в последней строке. При этом должно выполнятся условие
и их сумма ставится в последней строке. При этом должно выполнятся условие 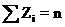 .
.
Выбираем условный нуль А, совпадающий с тем значением 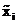 , которое соответствует среднему классовому промежутку, а если таковых два, то тому из них, который имеет большую частоту Zi.
, которое соответствует среднему классовому промежутку, а если таковых два, то тому из них, который имеет большую частоту Zi.
Строке табл. 1, соответствующей условному нулю А (у нас это строка 4, 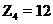 ,
, 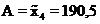 ), соответствует ai = 0, строки над этой имеют соответственно ai-1 = - 1, ai-2 = - 2, и т. д., а строки под i-й - ai+1 = 1, ai+2 = 2, ai+3 = 3 и т.д. После этого заполняются столбцы 6 - 9, а затем последняя строка – «Сумма» – для этих столбцов.
), соответствует ai = 0, строки над этой имеют соответственно ai-1 = - 1, ai-2 = - 2, и т. д., а строки под i-й - ai+1 = 1, ai+2 = 2, ai+3 = 3 и т.д. После этого заполняются столбцы 6 - 9, а затем последняя строка – «Сумма» – для этих столбцов.
Для нахождения оценок параметров распределения случайной величины Х сначала определяются начальные условные моменты mr.
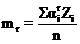 , (2)
, (2)
r = 1; 2; 3; 4.
Числители в для каждого момента уже получены в строке «сумма» таблицы 1. Оценка математического ожидания величины X – среднее арифметическое выборки – выражается через начальный условный момент первого порядка
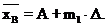 (3)
(3)
Центральные условные моменты определяются по формулам:
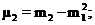 (4)
(4)
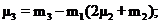 (5)
(5)
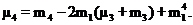 (6)
(6)
Оценки остальных числовых характеристик случайной величины Х выражаются через эти моменты:
- оценка среднего квадратичного отклонения
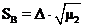 ; (7)
; (7)
- оценка коэффициента вариации




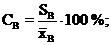
 (8)
(8)
- оценка коэффициента асимметрии
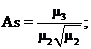 (9)
(9)
- оценка коэффициента эксцесса
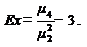 (10)
(10)
Находим начальные условные моменты
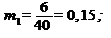
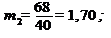
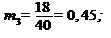
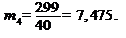
Тогда центральные условные моменты по формулам будут равны:
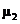 = 1,70 – 0,152 =1,6775;
= 1,70 – 0,152 =1,6775;
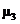 = 0,45 – 0,15 (2 – 1,6775 + 1,70) = - 0,308;
= 0,45 – 0,15 (2 – 1,6775 + 1,70) = - 0,308;
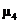 = 7,475 – 2 × 0,15 (- 0,308 + 0,45) +0,154 = 7,433.
= 7,475 – 2 × 0,15 (- 0,308 + 0,45) +0,154 = 7,433.
Теперь находим оценки параметров распределения прочности пряжи:
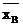 = 191,5 + 0,15 × 30 = 195,0 мН;
= 191,5 + 0,15 × 30 = 195,0 мН;
 ;
;
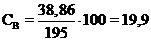 ;
;
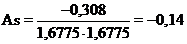
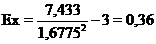
Для нормальной случайной величины коэффициенты асимметрии и эксцесса равны нулю. Так как оценки параметров – это их приближённые значения, найденные по результатам обработки выборки, то они могут, даже для выборки из нормальной генеральной совокупности, несколько отличаться от нуля. Поэтому считается, что если 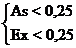 , то распределение умеренно отличается от нормального. Если же
, то распределение умеренно отличается от нормального. Если же 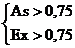 , то отличие от нормального распределения значительное.
, то отличие от нормального распределения значительное.
По асимметрии распределение умеренно отличается от нормального, а по эксцессу – незначительно.
Для определения теоретических частот нормального закона распределения используются таблицы функции
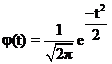 (11)
(11)
(Гмурман В. Е. Теория вероятностей и математическая статическая статистика, М., 2005.). Составим таблицу теоретических значений (табл. 2).
Первые два столбца табл. 2 соответствуют третьему и четвертому столбцам табл. 1. Для каждого 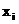 определяется нормированное отклонение ti:
определяется нормированное отклонение ti:
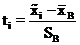 , (12)
, (12)
Таблица 2
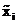 | 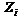 | 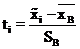 | 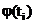 | 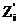 | 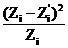 |
| Сумма | 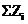 | - | 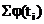 | 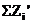 | 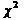 |
которое вносится в столб. 3 табл. 2. Затем находят по указанным таблицам значения функции (11) и записывают их в столб. 4. Теоретические частоты пропорциональны плотности нормального распределения (11). Коэффициент пропорциональности 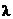 определяется так, чтобы сумма теоретических частот равнялась объёму выборки, т. е.
определяется так, чтобы сумма теоретических частот равнялась объёму выборки, т. е.
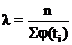 . (13)
. (13)
Тогда теоретические частоты Zi’ определяются по формуле
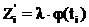 . (14)
. (14)
Для контроля вычислений следует проверить выполнение равенства
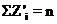 .
.
Так как теоретические частоты определяются по формуле (14) приближенно (рекомендуется находить их с точностью 0,01), то 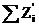 может отличаться от объема выборки на 0,01 – 0,02. В последний столбец вносят значения относительных квадратов отклонений фактических частот от теоретических и находят их сумму
может отличаться от объема выборки на 0,01 – 0,02. В последний столбец вносят значения относительных квадратов отклонений фактических частот от теоретических и находят их сумму
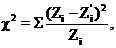 (15)
(15)
которая сравнивается с табличным значением 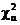 , определяемым по уровню значимости α и числу степеней свободы
, определяемым по уровню значимости α и числу степеней свободы 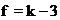 по таблицам распределения Пирсона (Гмурман В. Е.,С. 358), где k - фактическое число классовых промежутков; α - уровень значимости.
по таблицам распределения Пирсона (Гмурман В. Е.,С. 358), где k - фактическое число классовых промежутков; α - уровень значимости.
Составим таблицу 2.
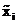 | 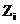 | 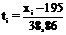 | 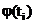 | 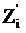 | 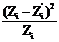 |
| 100,5 130,5 160,5 190,5 220,5 250,5 280,5 | -2,432 -1,660 -0,888 -0,116 0,656 1,428 2,200 | 0,02074 0,10062 0,26900 0,39628 0,32167 0,14387 0,03546 | 0,644 3,126 8,356 12,310 9,993 4,469 1,102 | 0,197 0,050 0,015 0,008 0,000 0,063 0,009 | |
| Сумма | - | 1,28764 | 40,000 | 0,342 |
Если 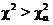 , то гипотеза о нормальности распределения отвергается. При этом вероятность отвергнуть верную гипотезу не превышает α.
, то гипотеза о нормальности распределения отвергается. При этом вероятность отвергнуть верную гипотезу не превышает α.
Если 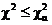 , то нет оснований отвергнуть гипотезу о нормальности распределения.
, то нет оснований отвергнуть гипотезу о нормальности распределения.
Коэффициент пропорциональности для нахождения теоретических частот
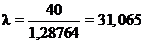 ,
,
что позволяет заполнить столб. 5. Расчётное значение критерия Пирсона 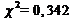 . Число степеней свободы f = 7 – 3 = 4. Выбираем уровень значимости α = 0,05 и по таблицам распределения Пирсона находим
. Число степеней свободы f = 7 – 3 = 4. Выбираем уровень значимости α = 0,05 и по таблицам распределения Пирсона находим 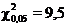 .
.
Так как 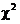 = 0,342 <
= 0,342 < 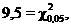 то нет оснований отвергнуть гипотезу о нормальности распределения прочности пряжи Т = 18,5 текс.
то нет оснований отвергнуть гипотезу о нормальности распределения прочности пряжи Т = 18,5 текс.
По данным столб. 1 и 2 строят на графике полигон частот. Для этого на график наносят точки 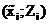 , которые соединяют ломаной линией. На том же графике строится теоретическая кривая Гаусса. Для этого наносят точки с координатами
, которые соединяют ломаной линией. На том же графике строится теоретическая кривая Гаусса. Для этого наносят точки с координатами 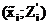 и дополнительную точку максимума, абсцисса которой равна
и дополнительную точку максимума, абсцисса которой равна 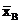 , а ордината определяется по формуле
, а ордината определяется по формуле 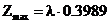 . Так как для
. Так как для 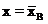
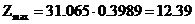 . Построенные точки соединяют плавной кривой (рис.1).
. Построенные точки соединяют плавной кривой (рис.1).
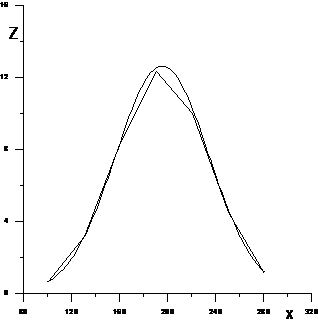
Рис. 1
Пример 2.Найти выборочное уравнение прямой регрессии Y на Х 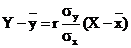 по данной корреляционной таблице .
по данной корреляционной таблице .
| Х Y | ny | ||||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | |||||
| - | - | ||||||
| - | - | - | |||||
| nx | n=100 |
Решение. Объем выборки n = 100.
Для того, чтобы написать уравнение прямой регрессии нам надо найти средние выборочные для Х и Y, дисперсии и коэффициент корреляции r.
Сначала найдем безусловные распределения величин X и Y. Для этого составим отдельные таблицы для каждой случайной величины
| Х | ||||||
| nx |
Находим среднее выборочное по формуле
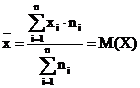
В нашем случае 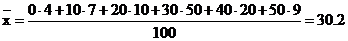
Находим дисперсию по формуле
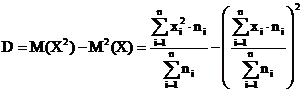
В нашем случае
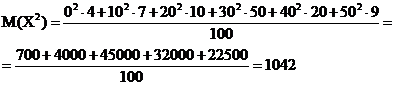
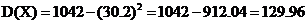
Следовательно 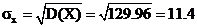
Аналогично, для случайной величины Y
| Y | |||||
| ny |
Находим среднее выборочное по формуле
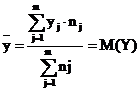
В нашем случае 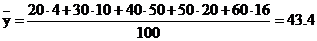
Находим дисперсию по формуле
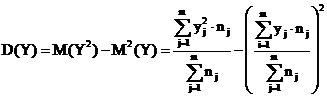
В нашем случае
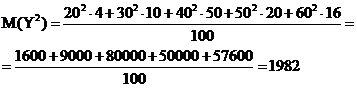
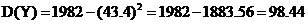
Следовательно 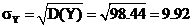 .
.
Коэффициент корреляции находим по формуле
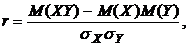 где
где 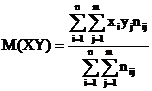 ,
, 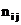 - частоты.
- частоты.
Найдем М(X Y)
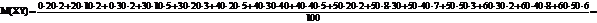
=1400
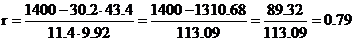
Так как коэффициент корреляции больше нуля, то между величинами X и Y существует прямая корреляционная зависимость (обратная, если коэффициент меньше нуля). Подставим найденные значения в уравнение регрессии
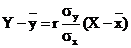
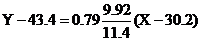 .
.
Раскроем скобки и приведем подобные члены