Биноминальный закон распределения.

ВВЕДЕНИЕ

Данные методические указания предназначены для проведения практических занятий по теме «Элементы тории вероятностей. Случайные величины». С целью облегчения самостоятельной работы студентов приводится большое количество подробно рассмотренных примеров для каждого занятия. Указания содержат варианты заданий для типовых расчетов.

Перед каждым практическим занятием следует изучить соответствующий материал по учебнику (или конспекту лекций) и ответить на относящиеся к занятию теоретические вопросы.

Занятие 1. Случайные величины. Виды случайных величин. Задание дискретной случайной величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

х x_l х₂ . . . х_п

р р₁ р₂ р_п

Пример 1.1.В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение. Напишем возможные значения X: х₁ = 0, x₂= 1, х₃ = 50. Вероятности этих возможных значений таковы:

р₁ = 0,01. р₂= 0,1, p₃= l-(p₁ + p₂) = 0.89.

Тогда искомый закон распределения

X
P	0,89	0,1	0,01

Контроль: 0,01+0,1+0,89=1.

Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (x_i, р_i),а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Пример 1.2. По мишени сделано 3 выстрела. Вероятность попадания при каждом выстреле равна р=0,6. За каждое попадание стрелку засчитывается по 5 очков. Построить ряд и многоугольник распределения случайной величины Х - числа выбитых очков.

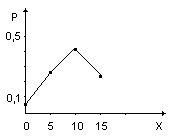Решение.Случайная величина принимает значения: 0, 5, 10, 15. Соответствующие вероятности

Р(х=0) =(1-р)³=0,064; Р(х=1)= 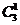(0,6)¹(0,4)²=

=3∙0,6∙0,16=0,288

Р(х=2)= 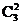(0,6)²(0,4)¹=0,432;

Рис.1 Р(х=3)=(0,6)³=0,216

Х
Р	0,064	0,288	0,432	0,216

Распределение Пуассона.

Пусть случайная величина Х принимает только целые неотрицательные значения: 0,1,2,…к,…. Теоретически последовательность этих значений может быть бесконечной. Если вероятность события Х=к Р(Х=х_к)= 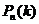определяется формулой

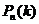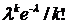= (к=0,1,2,…; а>0),

то случайная величина Х распределена по закону Пуассона ( 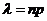− параметр распределения).

Пример 1.4. В единицу времени в среднем наблюдается а отказов сложной аппаратуры. Найти вероятность того, что за время Т будет к отказов.

Решение. В среднем за время Т будет аТ отказов. По формуле Пуассона:

Р (Х=к) = 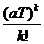е^-Та.

Если число испытаний велико, а вероятность события в одном испытании мала ( n>40, р<0,1), можно использовать формулу Пуассона.

Пример 1.5.Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.

Решение. По условию, n= 100 000, p= 0,0001 k= 5. События, состоящие в том, учебники сброшюрованы неправильно, независимы, число n велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона

=

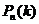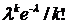
Найдем :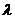

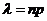= 100 000 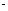0,0001=10

Искомая вероятность

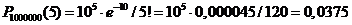
Задачи для самостоятельного решения

1.В партии 10%нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения случайной величины Х − числа нестандартных деталей среди отобранных и построить многоугольник полученного распределения.

2. На батарее имеется три снаряда. Стрельба ведется до первого попадания или пока не будут израсходованы все снаряды. Вероятность попадания при одном выстреле 0,8. Написать закон распределения случайной величины Х − числа израсходованных снарядов.

3. Написать закон распределения случайной величины Х − числа появления «герба» при двух бросаниях монеты.

4.Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения случайной величины Х − числа выпадений четного числа очков на двух костях.

5. В партии из 10 деталей имеются 8 стандартны Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.

6. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того , что за время Т откажут ровно три элемента.

Указание. Принять e 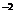=0,13534.

7. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно четыре бракованных.

8. Завод отправил на базу 500 изделий. Вероятность повреждения изделия во время пути равна 0,002. Найти вероятность того , что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.

Ответы: 6. 0,18; 7. 0,09; 8. 0,224

Решение.

1. Из условия 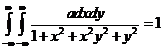найдем параметр a

=

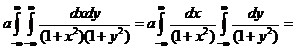
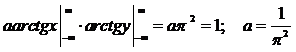
2.

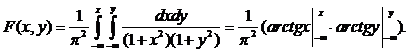
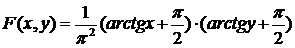
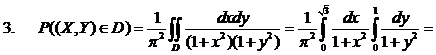
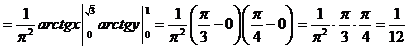
Чтобы найти плотность распределения случайной величины Х, входящей в систему (Х,Y), надо проинтегрировать двумерную плотность f(x,y) по всем возможным значениям случайной величины Y .

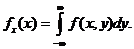Аналогично получается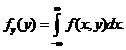

Обратно: по известным плотностям f_х (x) и f_у(y) найти плотность распределения f(x,y) системы в общем случае нельзя. Для решения этой задачи надо еще знать зависимость между этими величинами.

Случайные величины X и Y называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина, т.е. плотность распределения f(x,y) распадается на два множителя, один из которых зависит только от х, а другой только от у. В противном случае величины называются зависимыми.

Пример 5.3. Двумерная случайная величина (X,Y) задана плотностью распределения вероятностей

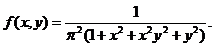. Являются ли случайные величины Х и Y зависимыми?

Решение.Преобразуемf(x,y) , разложив знаменатель на множител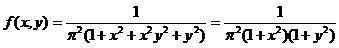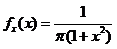и

;

и 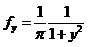, т.е. случайные величины X и Y независимы.

Пример 5.4. Двумерная случайная величина (X,Y) равномерно распределена внутри круга радиуса R с центром в начале координат, т.е. в области D: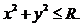

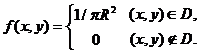
Проверить, будут ли величины X и Y независимы?

Решение.Найдем плотности распределения f_х(x) и f_у(y):

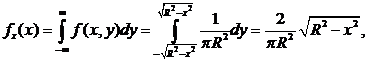
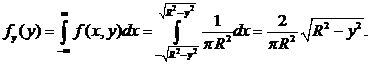
Теперь очевидно, что 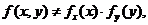т.е величины X и Y зависимы.

Задачи для самостоятельного решения

1. Двумерная случайная величина задана таблицей

Y	Х
0,5	0,1	0,3	0,25
1,5	0,15	0,15	0,05

Найти законы распределения составляющих.

2. Задана функция распределения двумерной случайной величины

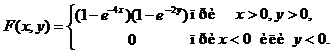
Найти двумерную плотность вероятностей системы.

Задачи для типовых расчетов

Задача 1. Дискретная случайная величина Х может принимать только два значения: х₁ и х₂, причем х₁<х₂. Известны вероятность р₁ возможного значения х₁, математическое ожидание М[X] и дисперсия D[X]. Найти закон распределения этой

случайной величины

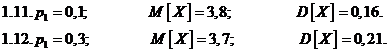
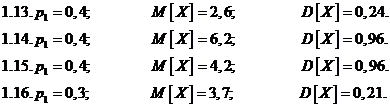
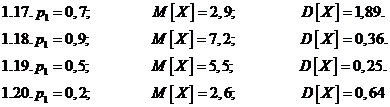
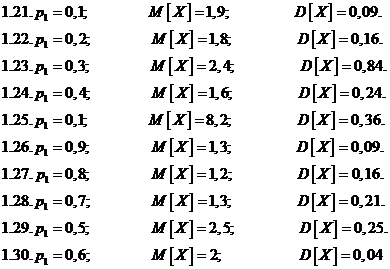
Задача 2.Дана плотность распределения f(x) случайной величины Х. Найти параметр а, функцию распределения случайной величины, математическое ожидание М[Х], дисперсию D[X], вероятность выполнения неравенства х₁<x< x₂, построить график функции распределения F(x) . (См. исходные данные)

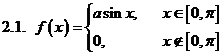
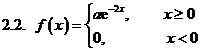
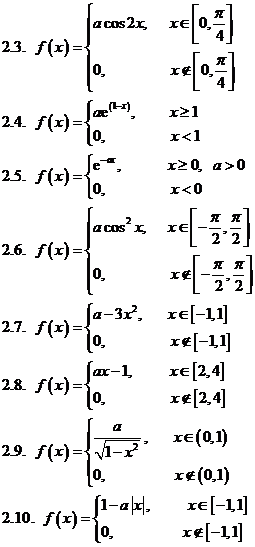
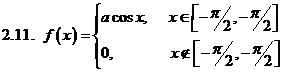
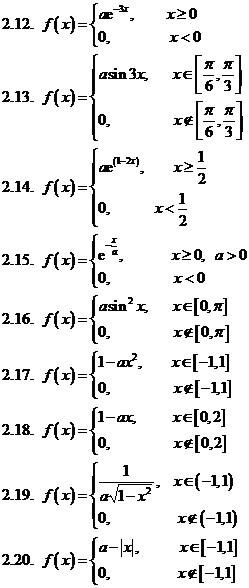
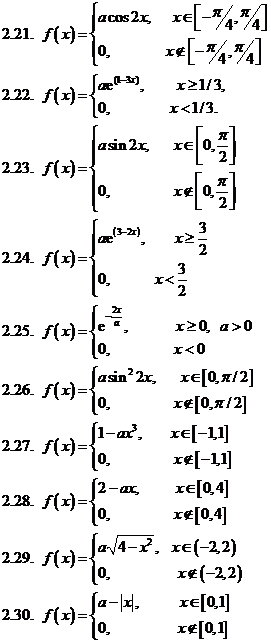
Задача 3. Дана плотность распределения p(x) случайной величины ξ. Найти параметр γ, математическое ожидание Мξ, дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения неравенства x₁<ξ<x₂. (См. исходные данные.)

Варианты 1-8: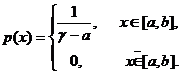

Варианты 9-16: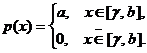

Варианты 17-24: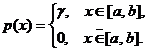

Варианты 25-31: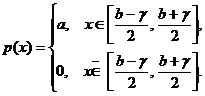

Задача 4.Плотность распределения вероятностей случайной величины ξ имеет вид 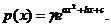Найти: γ, математическое ожидание Мξ, дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения неравенства x₁<ξ<x₂. (См. исходные данные.)

Задача 5. Найти вероятность попадания в заданный интервал (α,β) нормально распределенной случайной величины, если известны ее математическое ожидание а и среднее квадратическое отклонение σ (См. исходные данные в таблице).

Задача 6. Детали на производстве сортируются на 4 группы по величине отклонений от номиналов двух существенных параметров. Отклонения ранжируются. Ранги Х, У отклонений могут принимать лишь значения 0 и 1. Распределение двумерной случайной величины (Х,У) задано таблицей (См. исходные данные)

X \ Y

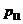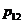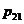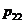Найти коэффициент корреляции 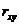называемый paнгoвым.

Задача 7. Двумерная случайная величина (Х, У) распределена равномерно в области D.

1. Составить плотность вероятности).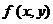

2. Найти .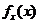

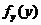3. Вычислить: , , , , .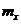

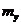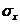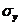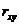4. Выяснить, зависимы или нет Х и У.

1. D − четверть кpyгa: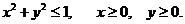

2. D − треугольник с вершинами 0(0, 0), А(1,0), В(0, 1).

3. D − четверть эллипса: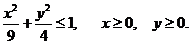

4. D − четверть эллипса: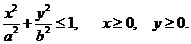

5. D − треугольник с вершинами А(1,0), В(1, 1), С(0, 1).

6. D − треyгольник с вершинами 0(0, 0), А(-1,0), В(0, -1).

7. D − полукруг: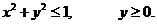

8. D − кpуг: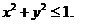

9. D − полукруг: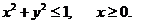

10. D − треугольник с вершинами А(-1,0), В(0, 1), С(1,0),

11. D − криволинейный треугольник, ограниченный линиями

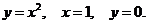
12. D − криволинейный треугольник, ограниченный линиями

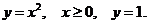
13 D − криволинейный треугольник, ограниченный линиями

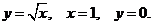
14. D − криволинейный треугольник, ограниченный линиями

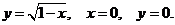
15. D − криволинейный треугольник, ограниченный линиями

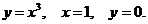
16. D − криволинейный треугольник, ограниченный линиями

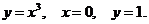
17. D − криволинейный треугольник, ограниченный линиями

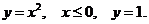
18. D −− криволинейный треугольник, ограниченный линиями

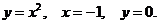
19. D − полукруг: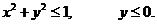

20. D − полукруг: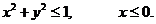

21. D − трапеция с вершинами А(0,0), В(0, 1), С(1, 1), D(2,0).

22. D − четверть кpyгa: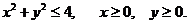

23. D − трапеция с вершинами А(0,0), В(0, -1), С(1, -1), D(2,0).

24. D − четверть кpyгa: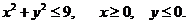

25. D − трапеция с вершинами А(2,0), В(3, 1), С(4, 1), D(4,0).

26. D − область, ограниченная линиями

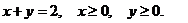
27. D − трапеция с вершинами А(0,0), В(0, 2), С(2, 2), D(4,0).

28. D − область, ограниченная линиями

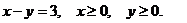
29. D − трапеция с вершинами А(0,0), В(0, -2), С(2, -2), D(4,0).

30. D − область, ограниченная линиями

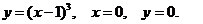
Задача 8. Дана плотность вероятности f(х,у). двумерной случайной величины (Х, У)

1. Найти значение параметра с .

2. Найти: .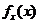

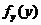3. Вычислить: , , , ,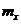

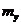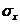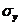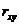
4. Выяснить, зависимы или нет Х, У.

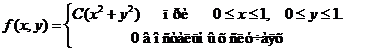
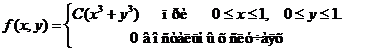
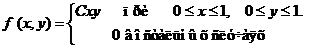
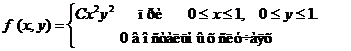
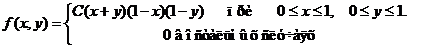
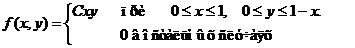
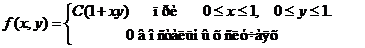
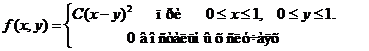
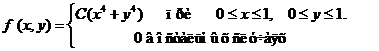
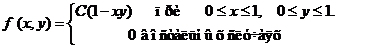
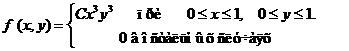
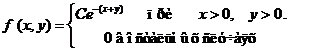
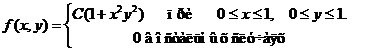
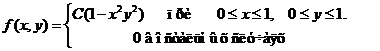
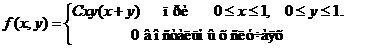
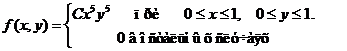
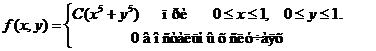
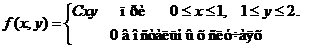
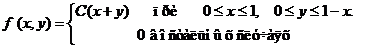
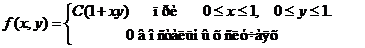
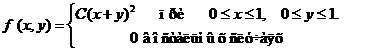
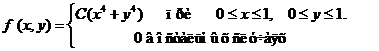
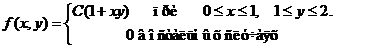
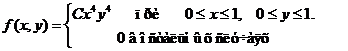
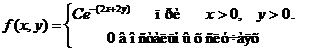
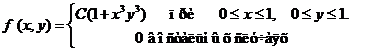
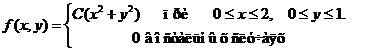
Исходные данные к расчетным заданиям

Вариант	Задача 2	Задача 3
х1	х2	a	β	x1	x2
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.	-2 π/6 -1 -π/6 -1 -1 -1 π/6 -1 -π/8 π/8 -1	π/2 π π π/4 π/2 π/3 π/8 π/4 π/4 1/2	2,5 1,5 1,5 -1 -2 -3 -1,5 -4 -3 -1 -1,5 -1,5 0,5 0,2 0,5 0,4 ¼ 0,02	2,5 3,5 2,5 1,8 2,4 3,5 2,8 2,8 2,6 4,8 -2 -1 1,5 1,5 -1	-0,7 -1,5 -2 -1 1,3 1,5 2,5 2,1 -1 1,5 4,5 -1 -2 -1 -1	3,3 2,6 2,3 2,8 1,1 0,3 1,6 2,5 0,5 0,5

Вари- ант	Задача 4
a	b	c	x1	x2
	-2 -2 -2 -4 -3 -4 -3 -3 -2 -3 -2 -2 -2 -4 -3 -4 -3 -3 -2 -3 -2 -4 -2 -4 -3 -3 -3 -3 -2 -2 -1	4/3 -8 -6 -3 -4 -4/3 4/3 -8 -6 -3 -4 -4/3 -8 -6 -4 -3 -4/3 4/3	-2 -2/3 -2 -2 2/3 -2 -1 -1 -1 -1 1/3 -1/3	1/3 -3/2 ½ -3/4 -1/2 1/3 -1/3 -1/3 1/3 -3/2 ½ -3/4 -1/2 1/3 -1/3 -1/3 -3/2 -3/4 ½ 1/3 -1/2 -1/3 -1/3 1/3 -1/3	2/3 -1 ¾ 3/2 ¼ 3/2 4/3 2/3 5/3 2/3 -1 ¾ 3/2 ¼ 3/2 4/3 2/3 5/3 ¾ -1 ¼ 3/2 4/3 3/2 5/3 2/3 2/3 4/3

Вариант	Задача 5	Задача 6
α	β	σ	a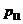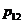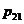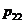
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.					0,94 0,8 0,03 0,2 0,2 0,2 0,5 0,4 0,45 0,1 0,2 0,05 0,1 0,25 0,35 0,25 0,06 0,25 0,85 0,3 0,92 0,4 0,9 0,7 0,1 0,2 0,1 0,35 0,2 0,8	0,01 0,05 0,05 0,1 0,2 0,1 0,1 0,2 0,3 0,2 0,4 0,1 0,05 0,1 0,15 0,2 0,24 0,1 0,02 0,15 0,02 0,1 0,04 0,05 0,1 0,1 0,2 0,15 0,3 0,1	0,02 0,01 0,02 0,1 0,1 0,2 0,2 0,3 0,1 0,1 0,1 0,05 0,05 0,2 0,05 0,1 0,14 0,15 0,03 0,05 0,01 0,2 0,01 0,05 0,1 0,1 0,3 0,2 0,25 0,05	0,03 0,05 0,9 0,6 0,5 0,5 0,2 0,1 0,15 0,6 0,3 0,8 0,8 0,45 0,45 0,45 0,56 0,5 0,1 0,5 0,05 0,3 0,05 0,2 0,7 0,6 0,4 0,3 0,25 0,05

Таблица значений функции ,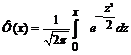

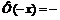
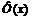
x
0,0	0,00000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0	0,49865	3,1		3,2		3,3		3,4
3,5		3,6		3,7		3,8		3,9
4,0
4,5
5,0

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие / В.Е. Гмурман. 12-е изд. М. : Высшее образование, 2008. - 479 с.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие / В.Е. Гмурман. 11-е изд., перераб. М. : Высшее образование, 2007. - 404 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов: в 2-х т. / Н.С. Пискунов. М.: Интеграл-Пресс, 2006. Т. 2.

4. Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для студентов втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2006. Ч. 2.

СОДЕРЖАНИЕ

Введение . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Занятие 1. Случайные величины. Виды случайных величин. . . . . . . . . . . . . Задание дискретной случайной величины. . . . . . . . 1

Занятие 2. Числовые характеристики дискретных случайных

величин. Функция распределения

дискретных случайных величин . . . . . . . . . . . 6

Занятие 3. Непрерывные случайные величины. Функция

распределения. Плотность распределения

вероятностей………………….. . . . . . . . . . . . . . . . .11

Занятие 4. Числовые характеристики непрерывных

случайных величин. Равномерное и нормальное

распределения непрерывных случайных величин.16

Занятие 5.Системы. случайных величин. . . . . . . . . . . . . . . . . 23

Занятие 6. Числовые характеристики системы . случайных

величин.Корреляционный момент. Коэффициент

корреляции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

Задачи для типовых расчетов . . . . . . . . . . . . . . . . . . .. . . . . . 33

Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по высшей математике по теме «Элементы

теории вероятностей. Случайные величины» для студентов специальностей 160201 “Самолето-

и вертолетостроение”, 130501 “Проектирование, сооружение и эксплуатация газонефтепроводов

и газонефтехранилищ” очной формы обучения

Составители:

Дурова Валентина Николаевна

Зайцева Марина Ивановна

Кузнецова Валентина Ивановна

Соколова Ольга Анатольевна

В авторской редакции

Компьютерный набор В.Н. Дуровой

Подписано в печать 08.12.2009

Формат 60x84/16. Бумага для множительных аппаратов.

Усл. печ. л. 3,1. Уч.- изд. л. 2,9. Тираж. 50 экз. “С”.

Зак. №

ГОУВПО « Воронежский государственный технический

университет»

394026 Воронеж, Московский просп., 14

ВВЕДЕНИЕ

Данные методические указания предназначены для проведения практических занятий по теме «Элементы тории вероятностей. Случайные величины». С целью облегчения самостоятельной работы студентов приводится большое количество подробно рассмотренных примеров для каждого занятия. Указания содержат варианты заданий для типовых расчетов.

Перед каждым практическим занятием следует изучить соответствующий материал по учебнику (или конспекту лекций) и ответить на относящиеся к занятию теоретические вопросы.

Занятие 1. Случайные величины. Виды случайных величин. Задание дискретной случайной величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

х x_l х₂ . . . х_п

р р₁ р₂ р_п

Пример 1.1.В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение. Напишем возможные значения X: х₁ = 0, x₂= 1, х₃ = 50. Вероятности этих возможных значений таковы:

р₁ = 0,01. р₂= 0,1, p₃= l-(p₁ + p₂) = 0.89.

Тогда искомый закон распределения

X
P	0,89	0,1	0,01

Контроль: 0,01+0,1+0,89=1.

Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (x_i, р_i),а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Пример 1.2. По мишени сделано 3 выстрела. Вероятность попадания при каждом выстреле равна р=0,6. За каждое попадание стрелку засчитывается по 5 очков. Построить ряд и многоугольник распределения случайной величины Х - числа выбитых очков.

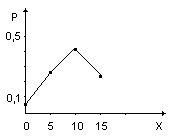Решение.Случайная величина принимает значения: 0, 5, 10, 15. Соответствующие вероятности

Р(х=0) =(1-р)³=0,064; Р(х=1)= 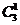(0,6)¹(0,4)²=

=3∙0,6∙0,16=0,288

Р(х=2)= 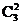(0,6)²(0,4)¹=0,432;

Рис.1 Р(х=3)=(0,6)³=0,216

Х
Р	0,064	0,288	0,432	0,216

Биноминальный закон распределения.

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р. Рассмотрим в качестве дискретной случайной величины X- число появлений события А в этих испытаниях.

Формула Бернулли 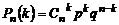является аналитическим выражением искомого закона распределения.

Напишем биномиальный закон в виде таблицы:

X	n	n-1	. . .	k	. . .
Р	рп	прп-1q	. . .	Ckn рkqn-k	. . .	qn

Пример 1.3.Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X — числа выпадений «герба».

Решение. Вероятность появления герба в каждом бросании монеты р=1/2, следовательно, вероятность не появления герба q=1 – 1/2=1/2.

При двух бросаниях монеты герб может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения Х таковы: х₁ = 0, x₂=l, x₃ =2. Найдем вероятности этих возможных значений по формуле Бернулли:

Р₂(0)= С⁰₂q²=(1/2)²=0,25,

Р₂(1)= С¹₂рq= 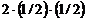=0,5,

Р₂(2)=С²₂ р²=(1/2)²=0,25.

Напишем искомый закон распределения:

X
P	0,25	0,5	0,25

Контроль: 0,25 + 0,5+0,25=1.

Распределение Пуассона.

Пусть случайная величина Х принимает только целые неотрицательные значения: 0,1,2,…к,…. Теоретически последовательность этих значений может быть бесконечной. Если вероятность события Х=к Р(Х=х_к)= 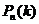определяется формулой

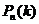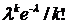= (к=0,1,2,…; а>0),

то случайная величина Х распределена по закону Пуассона ( 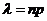− параметр распределения).

Пример 1.4. В единицу времени в среднем наблюдается а отказов сложной аппаратуры. Найти вероятность того, что за время Т будет к отказов.

Решение. В среднем за время Т будет аТ отказов. По формуле Пуассона:

Р (Х=к) = 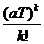е^-Та.

Если число испытаний велико, а вероятность события в одном испытании мала ( n>40, р<0,1), можно использовать формулу Пуассона.

Пример 1.5.Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.

Решение. По условию, n= 100 000, p= 0,0001 k= 5. События, состоящие в том, учебники сброшюрованы неправильно, независимы, число n велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона

=

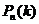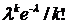
Найдем :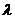

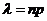= 100 000 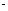0,0001=10

Искомая вероятность

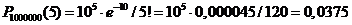
Задачи для самостоятельного решения

1.В партии 10%нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения случайной величины Х − числа нестандартных деталей среди отобранных и построить многоугольник полученного распределения.

2. На батарее имеется три снаряда. Стрельба ведется до первого попадания или пока не будут израсходованы все снаряды. Вероятность попадания при одном выстреле 0,8. Написать закон распределения случайной величины Х − числа израсходованных снарядов.

3. Написать закон распределения случайной величины Х − числа появления «герба» при двух бросаниях монеты.

4.Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения случайной величины Х − числа выпадений четного числа очков на двух костях.

5. В партии из 10 деталей имеются 8 стандартны Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.

6. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того , что за время Т откажут