Особенности применения математических методов для решения социологических задач.
Особенности применения математических методов для решения социологических задач.
1.. Создание прогностических моделей соц-го развития общества на
ближайшую и более отделенную переспективу.
2.. Выработка системы показателей и индикаторов соц-го развития.
3.. Разработка научных принципов и методик изучения связи
показателей соц-го, экон-го и эколог-го развития России.
История и перспективы информатизации социологических исследований.
· Методы дескритивности статистики:
- Метод оценки средних величин и их отклонений.
- Метод аналитических группировок индексный метод анализа.
· Проблемы: Репрезентативность выборки
· Развитие: Применение вычислительности техники.
Понятие признака в социологическом исследовании. Типы признаков.
Измерение - определение понятия. Измерение в социологии.
Измерение –это процедура, с помощью который измеряемый объект сравнивается с которыми эталоном и получает числовое выражение в определенном масштабе или шкале.
При помощью которой объект исследования рассматриваемые как носители определенных отношений между ними и как таковые составляющие эмпирическую систему отображаются в некоторую математическую систему с соответствующими отношениями между ее элементами.
Шкалирование как метод измерения социальных характеристик. Типы и виды шкал.
Шкала –правило, определения, каким образом в процессе измерения каждому изучаемому объекту ставится в соответствие некоторое число или другой математический конструкт. С помощью шкалы к каждому объекту ставится в соответствие число называемое шкальным значение объекта.
Процесс получения шкальных значений наз-ется шкалированием.
Типы и виды шкал.
Номинальные шкалы:
· Номинальное шкала (неупорядоченная шкала наименований)
· Частично упорядоченная номинальная шкала.
· Порядковая шкала или полностью упорядоченная ординарная шкала (шкала рангов)
Метрические шкалы:
· Интергальная шкала (шкала равных интергалов)
· Идеальная или абсолютная шкала (шкала пропорциональных оценок)
Дискретная случайная величина: определение, закон распределения, функция распределения.(стр. 194)
Закон распределения дискретной случайной величин Х наз-ется соответствие между каждым ее возможным значением Х1 и вероятностью ее появления р1
Фунций распределения вероятностей дискретной случайной величины Х наз-ется функция F(х) определения для каждого значения х вероятность того, что случайная величина х примет значение, меньше х:
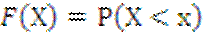
Закон распределения случайной величины. Примеры простых распределений, их формальное и графическое представление. (стр194)
Биномиальный закон распределения. (стр.195)
Ряды распределения, их разновидности.(196,200)
Закон распределения Пуассона. (см вопрос 9)
19. Математическое ожидание непрерывной случайной величины: определения, свойства, формулы для вычисления 202
Математическое ожидание непрерывной случайной величины М(х) удовлетворяет равенству:
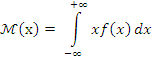
20. Дисперсия дискретной непрерывной величины: определения, свойства, формулы для вычисления. 202
21. Среднее квадратическое отклонение непрерывной случайной величины: определения, свойства, формулы для вычисления.202
22. Специфика и проблемы использования математики для решения социологических задач. (235 возможно!!)
Определения.
Выборочным уравнением линейной (прямой) регрессии У на Х является ур-е вида:
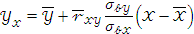
Выборочным уравнением линейной регрессии Х на У является ур-е вида:
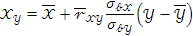
Выборочные средние
Выборочные средние квадратические отклонения
Выборочные коэф-т корреляции
Числа наз-ются выборочными коэф-тами регрессии У на Х или Х на У соотвественно:
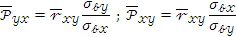
Особенности применения математических методов для решения социологических задач.
1.. Создание прогностических моделей соц-го развития общества на
ближайшую и более отделенную переспективу.
2.. Выработка системы показателей и индикаторов соц-го развития.
3.. Разработка научных принципов и методик изучения связи
показателей соц-го, экон-го и эколог-го развития России.
