Понятие критерия. Критическая область и область принятия гипотезы. Односторонняя и двусторонняя критическая область, критические точки. Мощность критерия.

Статистический критерий — случайная величина R с известным законом распределения, служащая для проверки нулевой гипотезы.

Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают.

Так как критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы. Такие точки называются критическими точками.

Различают одностороннюю (правостороннюю левостороннюю) и двустороннюю критические области.

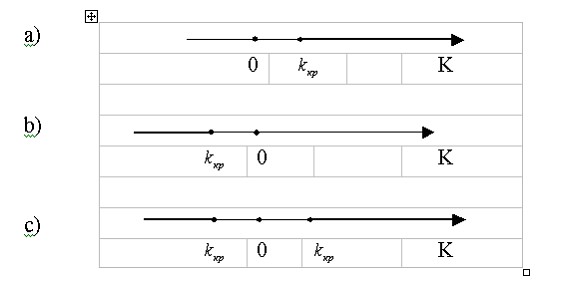
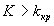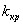Правосторонней(а) называют критическую область, определяемую неравенством , где – положительное число.

Левосторонней(b)называют критическую область, определяемую неравенством 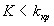, где 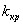– отрицательное число.

Двусторонней(c) называют критическую область, определяемую неравенствами 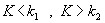, где 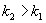. В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами 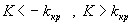или равносильным неравенством .

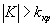Мощностью критерия называется вероятность попадания критерия в критическую область, при условии, что верна конкурирующая гипотеза (т.е. гипотеза противоположная нулевой).
52. Законы распределения "хи-квадрат", Стьюдента, Фишера.

χ²-распределение, хи-квадрат распределение, с n степенями свободы - распределение вероятностей, заданное плотностью вероятностей

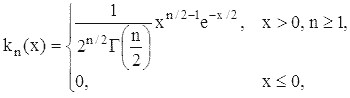
где Γ(λ) - гамма-функция.

Случайная величина 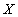имеет распределение хи-квадрат с 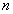степенями свободы, если плотность ее распределения имеет вид:

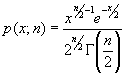
Хи-квадрат распределение с n степенями свободы может быть выведено как распределение суммы квадратов 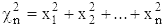n независимых случайных величин x₁, x₂, ..., x_n, имеющих стандартное нормальное распределение с параметрами 0 и 1. Сумма независимых случайных величин 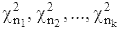с n₁, n₂, ..., n_k степенями свободы, соответственно, подчиняется хи-квадрат распределению с n = n₁ + n₂ + ... + n_k степенями свободы.

Сумма независимых случайных величин, имеющих распределение хи-квадрат, тоже подчинена закону распределения хи-квадрат с числом степеней свободы, равной сумме степеней свободы случайных величин, составляющих сумму.

Распределение Стьюдента

Пусть случайная величина x имеет стандартное нормальное распределение, а случайная величина c _n² - c ²-распределение с n степенями свободы.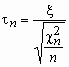

Если x и c _n² - независимы, то про случайную величину говорят, что она имеет распределение Стьюдента с n степенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:

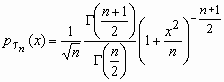, x R,Mt _n = 0,Dt _n = n/(n-2), n>2.

При больших n распределение Стьюдента практически не отличается от N(0, 1).

Распределение Фишера

Пусть случайные величины c _n²и c _m² независимы и имеют распределение c ² с n и m степенями свободы соответственно.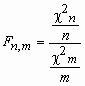

Тогда о случайной величине говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:

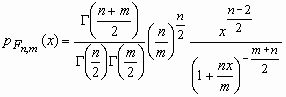, x>0,

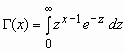- гамма-функция Эйлера;

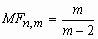, m>2; 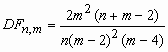, m > 4.
53. Критерии и правила проверки гипотез: о равенстве дисперсий и математических ожиданий двух нормальных генеральных совокупностей; о том, что генеральная совокупность распределена по нормальному закону.