Центральная предельная теорема.

Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.

Классическая формулировка Ц.П.Т.

Пусть 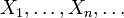есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние, 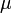и 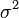соответственно. Пусть 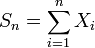Тогда:

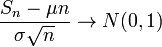по распределению при .

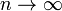Где 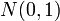— нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом 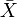выборочное среднее первых 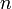величин, то есть 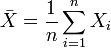мы можем переписать результат центральной предельной теоремы в следующем виде:

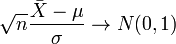по распределению при .

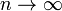Ц.П.Т. Ляпунова

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины 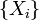имеют конечный третий момент. Тогда определена последовательность 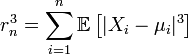Если предел 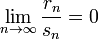(условие Ляпунова), то

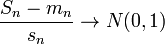по распределению при .

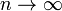38)Закон больших чисел.

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Слабый закон больших чисел

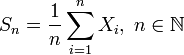
Тогда, .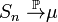

Усиленный закон больших чисел

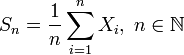
Тогда, .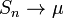

Неравенство Чебышева

p( | X – M(X)| < ε ) ≥ D(X) / ε².

Доказательство. Пусть Х задается рядом распределения

Х	х1	х2	…	хп
р	р1	р2	…	рп

Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).

D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые kслагаемых. Тогда

D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).

Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требовалось доказать

Теорема Чебышева: