Нормальное распределение или распределение Гаусса (непрерывное)

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Плотность распределения:

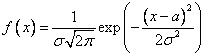
Числовые характеристики: , ,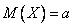

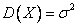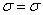
Пример плотности распределения:

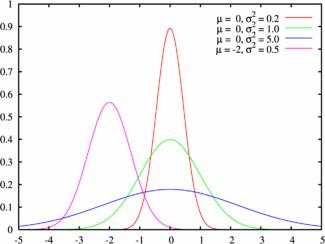
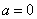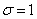Нормальный закон распределения случайной величины с параметрами и называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.

Функция Лапласа .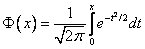

Вероятность попадания нормально распределенной случайной величины 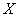в заданный интервал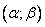

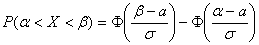
Вероятность отклонения нормально распределенной случайной величины 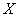на величину 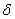от математического ожидания (по модулю).

.

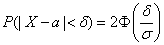Функцией распределения случайной величины 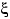мы назвали функцию 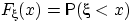. Основные свойства этой функции заключены в теореме:

Теорема 20. Любая функция распределения обладает следующими свойствами:

(F1)

она не убывает: если 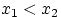, то ;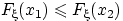

(F2)

cуществуют пределы 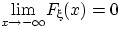и ;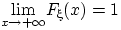

(F3)

она в любой точке непрерывна слева: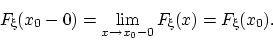

27. Дискретная случайная величина. Способы задания закона распределения дискретной случайной величины.

Говорят, что задана дискретная случайная величина 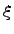, если указано конечное или счетное множество чисел

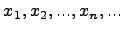
и каждому из этих чисел 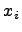поставлено в соответствие некоторое положительное число 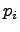, причем

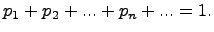
Числа 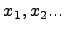называются возможными значениями случайной величины 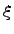, а числа 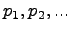- вероятностями этих значений ( ).

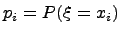Таблица

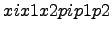
называется законом распределения дискретной случайной величины .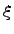

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки 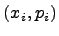и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины .

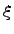Если возможными значениями дискретной случайной величины 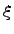являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:

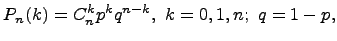
то говорят, что случайная величина 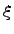имеет биномиальный закон распределения:

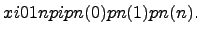
Пусть заданы натуральные числа m, n, s, причем 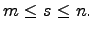Если возможными значениями дискретной случайной величины 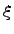являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле

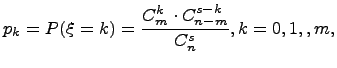
то говорят, что случайная величина имеет гипергеометрический закон распределения.

Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:

геометрический

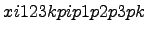
где ;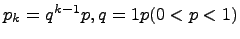

Закон распределения Пуассона:

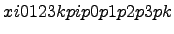
где

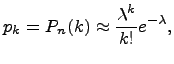
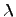- положительное постоянное.

Закон распределения Пуассона является предельным для биномиального при 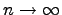, , 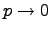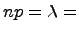. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:

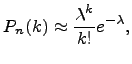
где 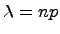.