Теорема умножения вероятностей: для двух произвольных событий; для двух независимых событий; для нескольких событий, независимых в совокупности.

Для двух произвольных событий

Вероятность произведения двух произвольных событий равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое имеет место, т.е.

P(AB) = P(A)P(B|A) = P(B)P(A|B).

Следствие. Для любых двух событий А и В справедливо равенство

P(A)P(B|A) = P(B)P(A|B).

Теорема умножения произвольных событий допускает обобщение на случай нескольких событий.

Для двух независимых событий

Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий:

P(AB) = P(A)P(B).

Для нескольких событий, независимых в совокупности.

Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий:

P(A₁ x A₂ x...x A_n) = P(A₁) x P(A₂) x...x P(A_n).

Формула полной вероятности. Вероятность события В, появляющегося в результате реализации одной и только одной гипотезы A_i(i = 1, 2,..., n) из некоторой группы несовместных гипотез A₁, A₂,..., A_n равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности события В, т.е.

,

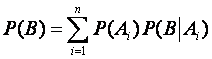причем .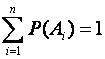

В теоретико-вероятностных приложениях часто требуется найти вероятность события A_i, если известно, что В произошло. Общая схема решения подобных практических задач сводится к применению формулы Байеса:

.

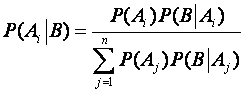Принцип использования формулы Байеса можно пояснить следующим образом.

Пусть событие В может быть реализовано в различных условиях, относительно характера которых можно сделать n гипотез: A₁, A₂,...,A_n.

По тем или иным причинам вероятности P(A_i) этих гипотез известны до испытания (априорные вероятности). Известно также, что гипотеза A_i сообщает событию В вероятность P(B|A_i). Произведен опыт, в котором событие В наступило. Это должно вызвать переоценку вероятностей гипотез A_i. Переоценка указанных вероятностей производится по формуле Байеса. Переоцененные вероятности гипотез называются апостериорными вероятностями.

Сама по себе формула Байеса теоретически бесспорна, но во многих случаях ее применения априорные вероятности P(A_i) неизвестны. Некоторые исследователи в таких случаях считают возможным предполагать равные вероятности всех гипотез A_i. Однако в общем случае такой подход неверен].

Другим выходом из проблемной ситуации, связанной с незнанием априорных вероятностей, явился метод последовательного применения формулы Байеса, когда апостериорные вероятности многократно пересчитываются и на каждом последующем шаге используются как априорные. При этом неизвестные априорные гипотезы также принимаются равновероятными, но многократный пересчет значительно снижает влияние данного предположения на конечные.

Формула полной вероятности.

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

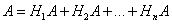
Применяя аксиому сложения вероятностей, имеем

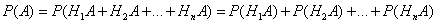
Но 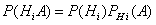(i=1, 2, ..., n), поэтому

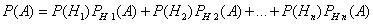Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

Теорема Байеса.

Теорема Байеса— позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны.

Формула Байеса:

,

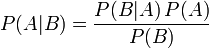где

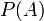— априорная вероятность (насколько вероятна причина вообще) гипотезы A

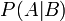— вероятность гипотезы A при наступлении события B

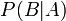— вероятность наступления события B при истинности гипотезы A

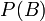— полная вероятность наступления события B.

Следствие

Формула Байеса является важным следствием из формулы полной вероятности события, зависящего от нескольких несовместных гипотез (и только от них!).

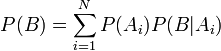— вероятность наступления события B, зависящего от ряда гипотез 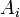, если известны степени достоверности этих гипотез (например, измерены экспериментально);

Формула Бернулли

Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна:

P_n(k)=C_n^kp^kq^n-k

или

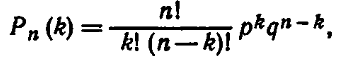
где q=1-p

Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, — находят соответственно по формулам:

P_n(0)+P_n(1)+...+P_n(k-1);

P_n(k+1)+P_n(k+2)+...+P_n(n);

P_n(k)+P_n(k+1)+...+P_n(n);

P_n(0)+P_n(1)+...+P_n(k);