Статическое определение вероятности.

Классическое опр вероятн предпологает, что число элементарн исходов испытания конечно. На практике же часто встречаются испыт-я, число возможных исходов которых бесконечно. Поэтому наряду с классич опр вероятн используют и др. опр. "Статистическое определение" В качестве статистической вероятности события принимают относительную частоту или число, бизкое к ней. Например, если в результате достаточно большого числа испытаний оказалось, что отностительная чистота весьма близка к числу 0,4 то это число можно принять за статическую вероятность события. Для сущетвования статич вероятн события А требуется: а) возможность производить неограниченное число испытаний, в каждом из кот событие А наступает или нет б) устойчивость относительных частот появления события А в различных сериях достаточно большого числа испытний. Недостатком стат опр явл. неоднозначность статич вероятности; например в качестве вероятности события можно принять не тольно 0,4 но и 0,39; 0,41 и т.д.

Рассмотрим случайный эксперимент, заключающийся в том, что подбрасывается

игральная кость, сделанная из неоднородного материала. Ее центр тяжести не

находится в геометрическом центре. В этом случае мы не можем считать исходы

(выпадение единицы, двойки и т.д.) равновероятными. Из физики известно, что кость

более часто будет падать на ту грань, которая ближе к центру тяжести. Как определить

вероятность выпадения, например, трех очков? Единственное, что можно сделать, это

подбросить эту кость n раз (где n-достаточно большое число, скажем n=1000 или

n=5000), подсчитать число выпадений трех очков n3 и считать вероятность исхода,

заключающегося в выпадении трех очков, равной n3/n - относительной частоте

выпадения трех очков. Аналогичным образом можно определить вероятности

остальных элементарных исходов — единицы, двойки, четверки и т.д. Теоретически

такой образ действий можно оправдать, если ввести статистическое определение

вероятности.

26) Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

P_n = n!,

где n! = 1 * 2 * 3 ... n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

A^m_n = n (n - 1)(n - 2) ... (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

С ^m_n = n! / (m! (n - m)!).

примеры перестановок, размещений, сочетаний

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

A^m_n = P_mC ^m_n.

Примеры:

1. Бросают игральную кость. Событие А — появление цифры 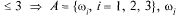— появление 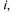т.е. в А входят 3 элементарных события.

2. Бросают две игральные кости. Пространство элементарных событий 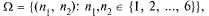число элементарных событий 36. Пусть А — появление таких цифр 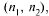что их сумма 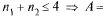{(1, 1), (1,2), (1, 3), (2, 1), (2, 2), (3, 1)}.

3. Из карточек сложено слово из шести букв «победа». Выбираем наугад две буквы, А — обе выбранные буквы являются согласными. Пространство элементарных событий состоит из 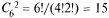элементарных событий. Случайное событие А состоит из 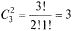элементарных событий.

27) События А и В, связанные с некоторым опытом, называются совместными, если существует испытание, при котором реализуются оба события.

События А и В, связанные с некоторым опытом, называются несовместными, если не существует испытания, при котором реализуются оба события.

Пример 1. Пусть опыт состоит в бросании игральной кости. Рассмотрим три связанных с этим опытом события:

А - число выпавших очков четное

В - число выпавших очков нечетное

С -число выпавших очков делится на три

Очевидно, что события А и В несовместны, так как не существует испытания, при котором выпавшее число очков будет одновременно и четным, и неетным.

События А и С совместны так как существует испытание (выпадение 6 очков), когда реализуется и А, и С.

События Ви С совместны так как существует испытание (выпадение 3очков), когда реализуется и В, и С.

Теперь проверьте все ли Вы поняли как нужно.

Упражнение 1.

Из колоды в 36 карт случайным образом извлекается одна карта. Рассматриваются три события:

А - извелеченная карта бубновой масти;

В - извлеченная карта - дама пик;

С - извлеченная карта - картинка.

Какие из пар событий А и В, А и С, В и С - совместны, а какие нет.(Решишь?)))

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах.

В частности, если два события А и B — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.

Пусть события A и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).