Теорема о вероятности суммы событий

ВОПРОС № 1

Предмет теории вероятности. Пространство элементарных событий. Алгебра событий

По форме проявления причинных связей, законы природы и общества делятся на 2 класса: детерминированные (подчиняющиеся определенным законам) и статистические (явления, результаты которых мы предсказать не можем). К статистическим явлениям применяют слово «вероятно».

Теория вероятности – это математическая наука, изучающая закономерности случайных явлений. Например, модель роста числа жителей даёт теория вероятности, а конкретные данные – это статистика.

На теорию вероятностей опирается математическая статистика, задача которой состоит в том, чтобы по ограниченным данным восстановить с определенной степенью достоверности характеристики, присущие генеральной совокупности (т.е. всему мыслимому набору данных, описывающему изучаемое явление).

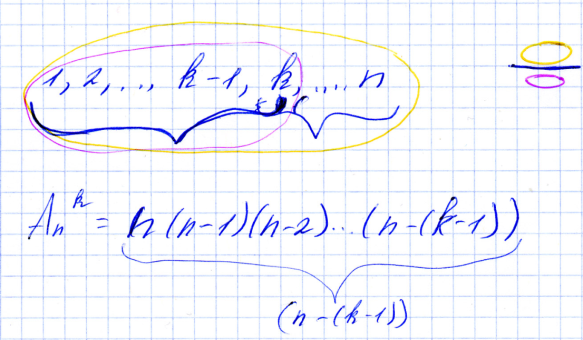
Определение

Событие называетсяслучайнымв данном опыте, если оно может произойти, а может и не произойти в этом опыте.

Все возможные в данном опыте исходы составляют множество Ω, которое называется пространством элементарных исходовили элементарных событий.

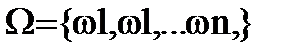
О. Событие– это произвольный набор элементарных исходов, или произвольное подмножество множества элементарных исходов Ω.

События обозначают латинскими буквами A, B, H… Для наглядности события изображают на диаграмме Венна. Геометрически она совершенно не верна, но удобна для демонстрации множеств.

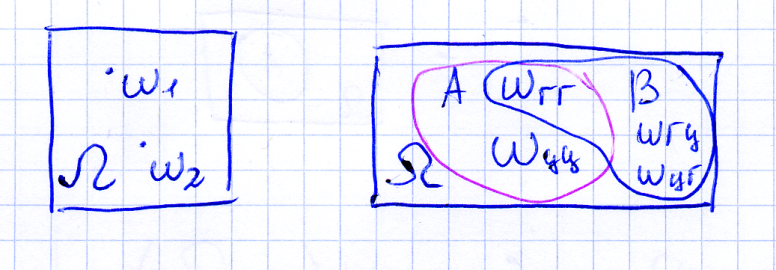
О. Событие, происходящее всегда ( при любом элементарном исходе ) называется достоверным и обозначается Ω.

О. Невозможноесобытие не происходит никогда (не содержит ни одного элементарного исхода). Обозначается как пустое множество .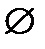

Действия над событиями

О. Пересечение (произведение) двух событий A и B называется событие C, происходящее тогда и только тогда, когда наступают одновременно 2 события A и B (состоящее из тех элементарных исходов, которые принадлежат и A, и B).

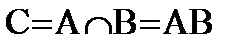
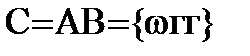
О. 2 события называются совместными, если они пересекаются.

О. 2 события называются несовместными, если они не пересекаются.

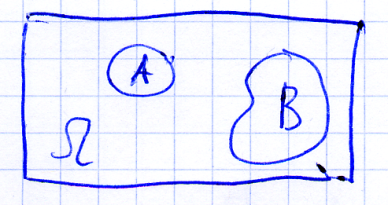
Два события называются противоположными, если появление одного из них равносильно непоявлению другого.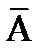

О. Объединением (суммой) 2х событий A и B называется событие C, происходящее тогда и только тогда, когда наступает хотя бы одно из событий A или B (состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из множеств.

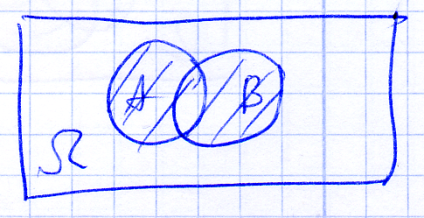
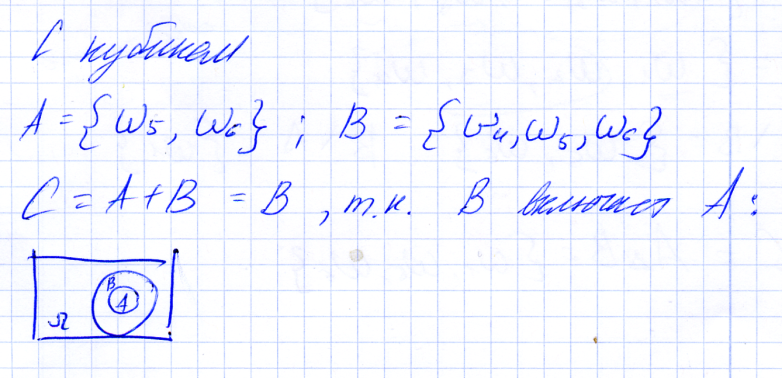
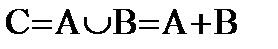
Сумма событий вовсе не означает сложение исходов!

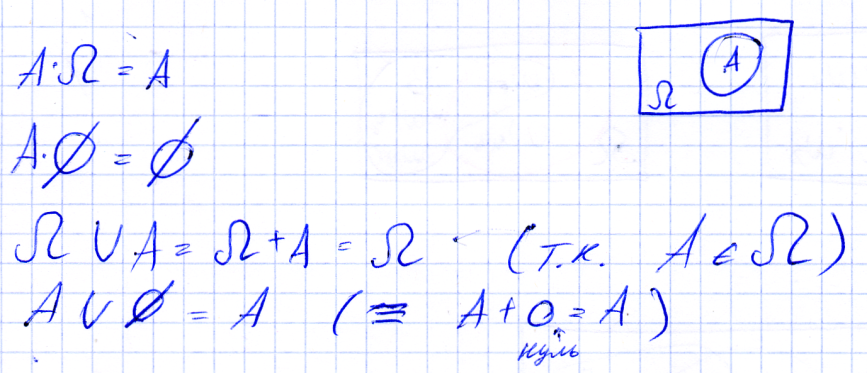
О. Разностью двух событий A и B называется событие C, происходящее тогда и только тогда, когда происходит событие A, но не происходит событие B (состоящее из тех элементарных исходов, которые принадлежат A, но не принадлежат B.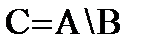

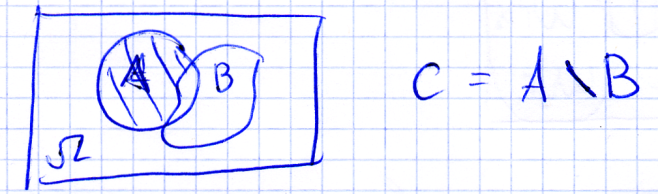
О. Симметрической разностью двух событий A и B называется событие C, представляющее объединение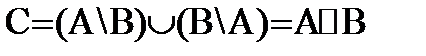

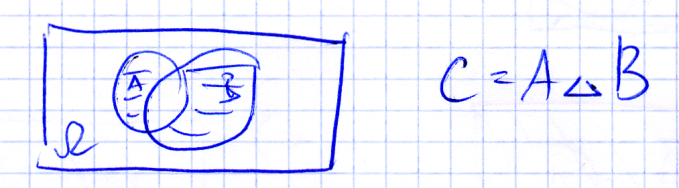
Пример

А: «Выпадение не менее 2х очков при бросании кубика». B: «Выпадение не более 4х очков» Найти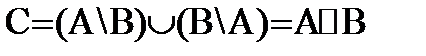

ДЗ:

Пользуясь диаграммой Венна, показать справедливость формул де Моргана.

О. 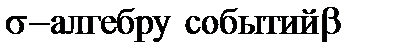можно определить как систему подмножеств пространства элементарных исходов Ω, замкнутую относительно счётного числа теоретико-множественных операций.

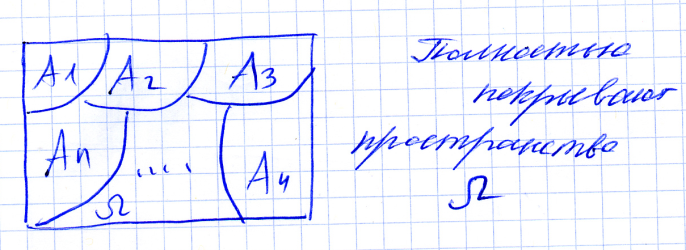
О. Множество событий A1, A2,…An называют полной группой событий, если они попарно несовместны и появление одного и только одного из них является достоверным событием.

ВОПРОС № 2

Элементы комбинаторики. Понятие случайного события. Классическое определение вероятности.

Комбинаторика изучает способы подсчёта числа элементов в различных конечных множествах.

Пример

ШПС

ШСП

ПШС

ПСШ

СШП

СПШ

Определение

Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Обозначаются перестановки P_n. P₃=6

Теорема

Число перестановок множества из n-ных элементов равно:

P_n=n! (факториал – произведение всех натуральных чисел начиная с единицы)

P_n=1∙2∙3∙…∙n

Пример:

1,2,3,4 Сколько можно составить двузначных чисел

12 13 14 21 23 24 31 32 34 41 42 43

Ответ: 12

Размещениями называют множества, выбранные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком.

Обозначение:

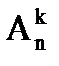
Число размещений из n элементов по k равно:

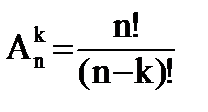
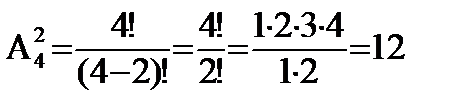
В хоккейном турнире участвуют 6 команд. Каждая команда должна сыграть с каждой 1 игру. Сколько игр сыгранно в турнире?

Определение

Сочетаниями из n различных элементов по k называются множества, которые отличаются хотя бы одним элементом. Обозначаются сочетания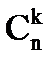

Теорема

Число сочетаний из n по k:

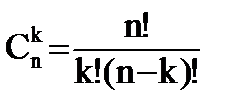
По определению 0!=1. Факториал относится к натуральным числам, поэтому считается, чо упорядочить 0 объектов можно единственным образом.

При решении задач комбинаторики используются следующие правила:

1. Правило суммы: если некоторый объект A может быть выбран из множества объектов m-способами, а другой объект B может быть выбран n-способами, то выбрать либо A, либо B можно m+n способами («или» это +)

2. Правило произведения: если некоторый объект A может быть выбран из множества объектов m-способами, и после каждого такого выбора объект B может быть выбран n-способами, то пара объектов AB в указанном порядке может быть выбрана m∙n способами («и» это ∙)

Принцип математической индукции –

Утверждение P(k) зависящее от натурального числа k справедливо при любом k из N, если утверждение P(k) справедливо при k=1

Для всякого l из N из справедливости P(l) следует справедливость P(l+1).

Лемма 1

Каково бы ни было целое число n≥1, число различных размещений по одному объекту из заданных n равно:

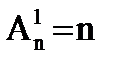
У нас n объектов. Мы можем выбрать каждый объект только одним способом.

Число 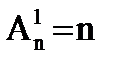есть суммарное число различных способов, какими один объект может быть выбран из n объектов. Выбранным может быть либо первый, либо второй, либо третий …. либо n-ый:

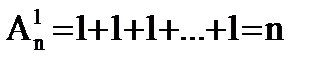
Лемма 2

Каковы бы ни были n≥2, 1<k≤n, число различных размещений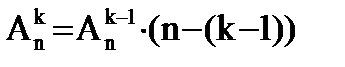

Доказательство:

1,2,3,…k-1,k,…n

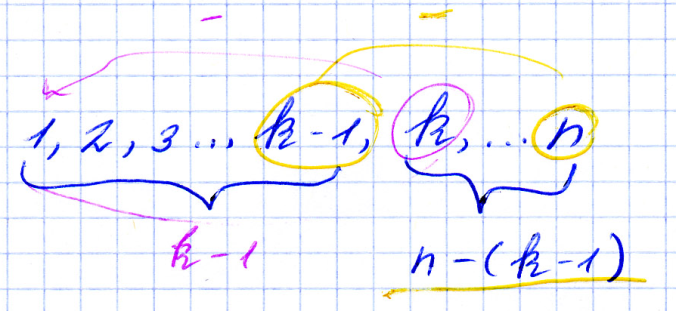
Пусть имеется размещение k-1 объектов из n объектов. В этом размещении имеется (k-1) упорядоченно размещенных объектов и (n-(k-1)) оставшихся неразмещенных объектов. На следующую k-тую позицию можно выбрать любой из оставшихся неупорядоченных объектов. Таким образом, каждому конкретному размещению (k-1) объектов из n можно поставить в соответствие (n-(k-1)) размещений k объектов из n. Это означает что A из n по k должно быть больше чем A из n по k-1 в (n-(k-1)) раз.

Теорема

Каковы бы ни были числа 1≤k≤n, число размещений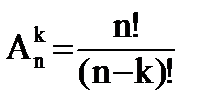

По второй лемме:

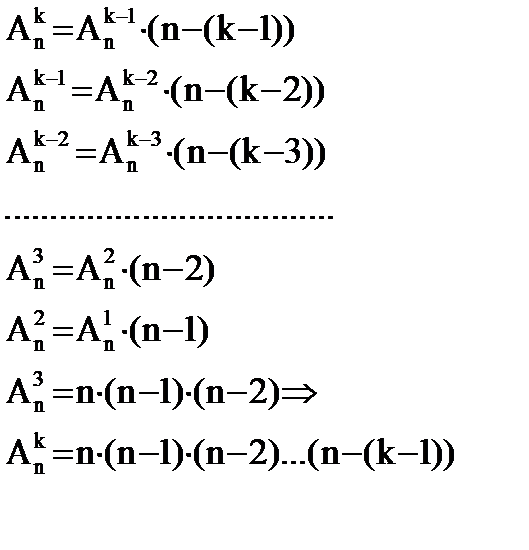
Определение

Событие называетсяслучайнымв данном опыте, если оно может произойти, а может и не произойти в этом опыте.

Все возможные в данном опыте исходы составляют множество Ω, которое называется пространством элементарных исходовили элементарных событий.

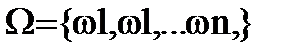
О. Событие– это произвольный набор элементарных исходов, или произвольное подмножество множества элементарных исходов Ω.

События обозначают латинскими буквами A, B, H… Для наглядности события изображают на диаграмме Венна. Геометрически она совершенно не верна, но удобна для демонстрации множеств.

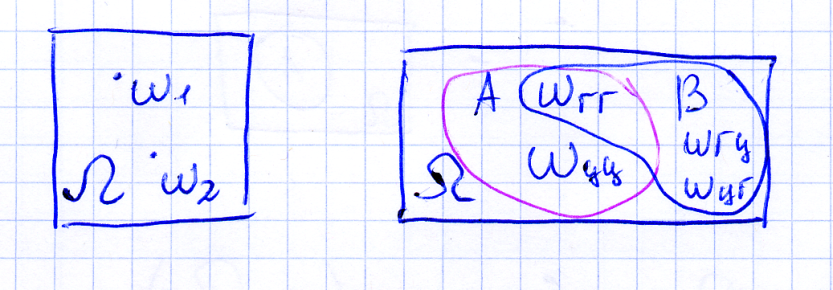
О. Событие, происходящее всегда ( при любом элементарном исходе ) называется достоверным и обозначается Ω.

О. Невозможноесобытие не происходит никогда (не содержит ни одного элементарного исхода). Обозначается как пустое множество .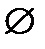

Классическое определение вероятности

О. События считают равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие.

О. Вероятностью события A называется отношения числа k благоприятных для события A благоприятных исходов к общему числу равновозможных элементарных исходов n.

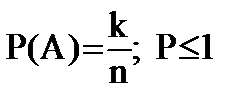
Всего 10 шаров, 4 синих, 6 красных. Вероятность вытащить синий: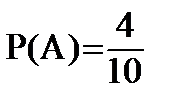

Свойства вероятности:

1) Вероятность достоверного события равна единице: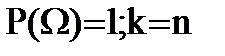

2) Вероятность невозможного события равна нулю: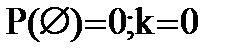

3) Вероятность случайного события заключена между нулем и единицей 0<P(A)<1

Вероятность любого события изменяется от нуля до единицы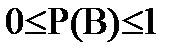

Свойство 1. Сумма вероятности двух противоположных событий равна единице

Пример:

Найдите вероятность того, что при бросании двух игральных кубиков в семе выпадет не менее 4 очков.

A: ”Не менее 4х очков в сумме при бросании 2х кубиков”

ВОПРОС № 3

Теорема о вероятности суммы событий. Условная вероятность. Теорема о вероятности произведения событий. Зависимые и независимые события.

Условная вероятность

Представим игру в кубик:

Если выпадет менее 4, ты выиграешь. Если нет – ничего. Белые грани – четные числа, красные – нечетные. Он увидел, что сверху – белая грань.

1, 2, 3

Только 2 – четное, значит, вероятность – 1/3.

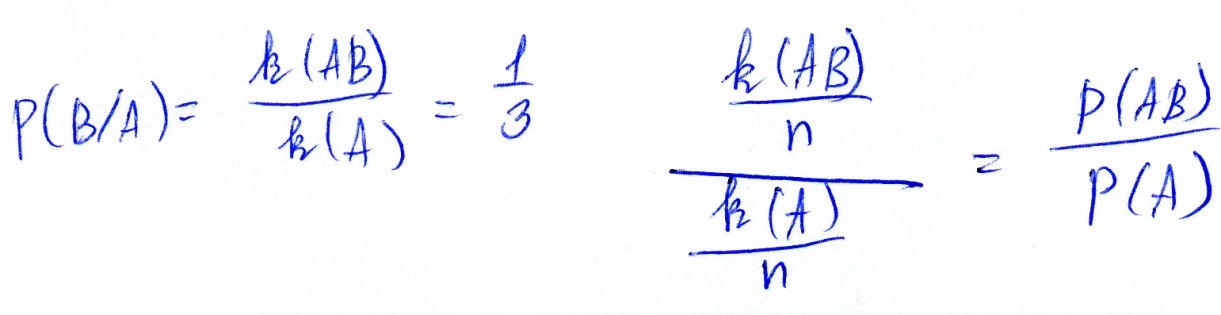О. Условной вероятностью события B при условии, что событие A произошло 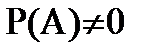, называется отношение вероятности пересечения событий A и B к вероятности события A.

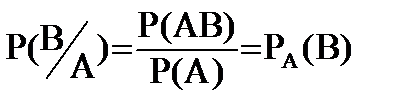
Пример

A – 4 или 6

B – 2, 4, 6

P(B/A) = 1 – достоверное событие

P(A/B)=2/3

P(Ω/A)=1; P(Ø/A)=0

Если события B и C несовместны, то вероятность P((B+C)/A)=P(B/A)+P(C/A)

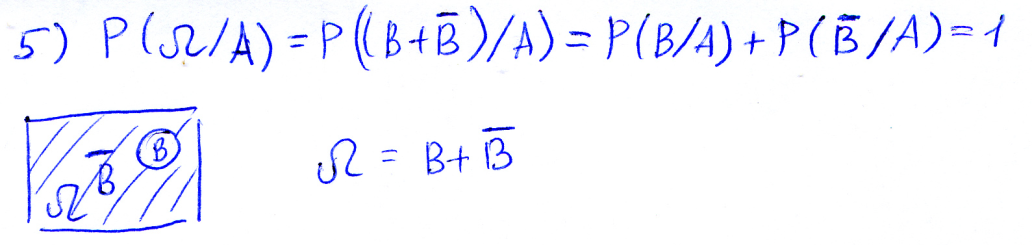
Независимые события.

О. События A и B называются независимыми, если условная вероятность события B при условии, если A произошло, равна безусловной вероятности события B:

P(B/A)=P(B)

P(AB)=P(A)*P(B/A)=P(A)*P(B)=P(AB)

Теорема

Если событие A и B независимые, то вероятность их произведения равна произведению вероятности этих событий.

О. События A1,A2,…An называются независимыми в совокупности, если они попарно независимы, а также независимы каждые из них и пересечение всех остальных n-1.

Теорема:

Если события A1, A2, … An независимы в совокупности, то вероятность их произведния равна произведению вероятности этих событий.

P(A1A2…An)=P(A1)P(A2)…P(An)

Пример

Зависимы ли события A и B, если они несовместны?

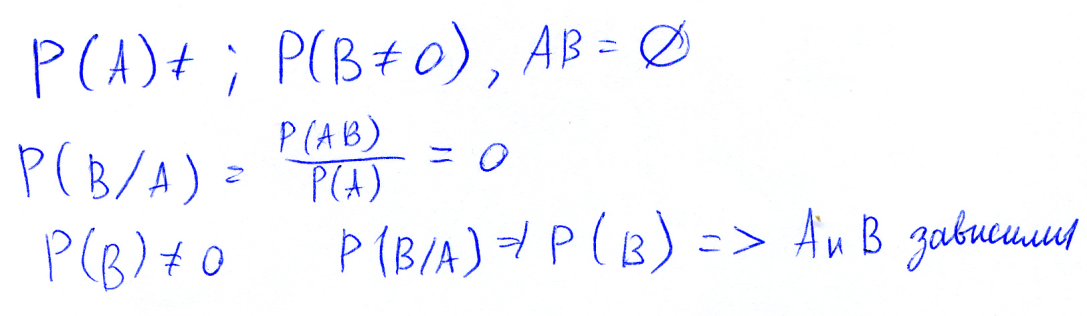
ВОПРОС № 4

Формула полной вероятности. Формулы Байеса. Априорная и апостериорная вероятности.

Пусть от первого предприятия поступило 20 изделий, от второго – 10, и от третьего – 70. Вероятности некачественного изготовления изделия на предприятиях соответственно равны 2/100 3/100 5/100

Определить вероятность получения некачественного изделия.

А: Бракованные изделия

P(A)=0,2*0,02+0,1*0,03+0,7*0,05=0,042=4,2%

Полученный процент всегда больше самого маленького и меньше самого большого.

Предположим, что в результате опыта может произойти одно из n несовместных и составляющих полную группу событий Hi. Пусть событие A может осуществиться лишь вместе с одним из событий H1, H2…Hn. Пусть также нам известны и вероятности P(H1),… P(Hn, P(A(H1)… , P(A(Hn)). Заранее не известно, с каким из событий Hi произойдет событие A, то события Hi называют гипотезами. Определим безусловную вероятность события A

Вероятности гипотез до проведения опыта называются априорными, а вероятности, вычисленные после опыта – апостериорными.

Считая, что до опыта были известны априорные вероятности P(H1),P(Hn) и условные вероятности P(A/H1)… , P(A/Hn), определим апостериорные вероятности:

Предприятие, производящее компьютеры, получает одинаковые чипы от двух поставщиков. Первый поставляет 65% чипов, второй – 35%. Известно, что качество поставляемых чипов разное. Первый – 98% качественных, второй – 95%. Предприятие осуществляет гарантийный ремонт компьютеров. Имея данные о числе компьютеров, поступающих на гарантийный ремонт всвязи с неисправностью чипов. Переоцените вероятности того, что возвращенный для ремонта компьютер укомплектован чипом от первого поставщика.

А: бракованный чип

ВОПРОС № 5

Геометрическое и статистическое определение вероятности

Геометрические вероятности – это вероятности попадания точки в область. Она пропорциональна мере данной области.

Пример

В круг, радиусом R=1 равномерно бросается точка. Найти вероятность события A, заключающегося в попадании этой точки в круг радиусом r=1/2

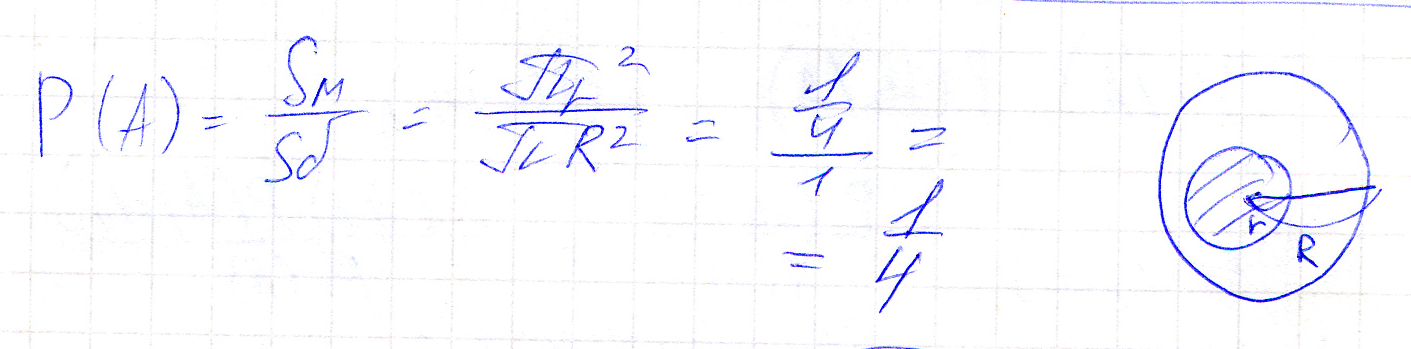Положение 1

Если все возможные событие могут быть изображены в виде точке на отрезке длиной L_общ, а события, благоприятные событию B могут быть изображены на отрезке длиной Lb, то

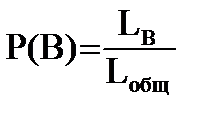
Если все возможные события могут быть изображены в виде точки на плоской фигуре площадью Sобщ, а события, благоприятные B, могут быть изображены на плоской фигуре площадью S_B, то вероятность

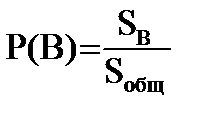
Если все возможные события могут быть изображены в виде точки в 3-х мерном пространстве внутри фигуры объёмом V общ, а события, благоприятные B в виде точки объёмом V_B, то вероятность события B: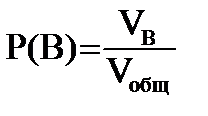

Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течении данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождение причала, если время стоянки первого парохода равно 1 часу, а второго – 2 часам.

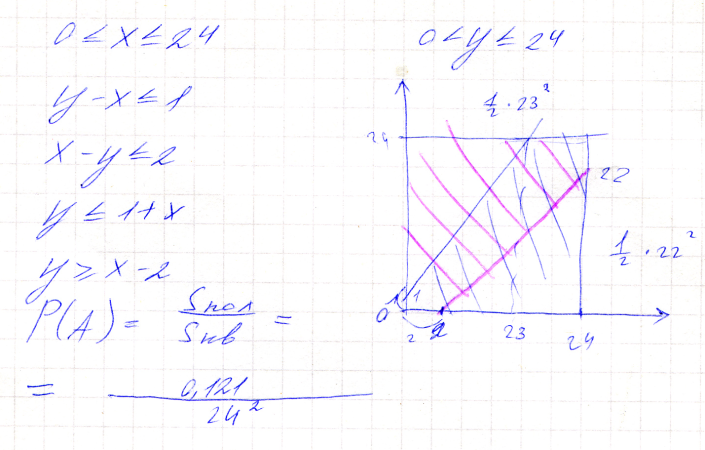
Пример

A: “Доллар дорожает”

H1 – активный эк.рост

H2 – умеренный

H3 – низкий

Свойства

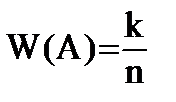
1) Частота случайного события заключена между 0 и 1

2) Относительная частота достоверного события равна 1

3) Относительная частота невозможного события равна 0

4) Частота суммы 2х несовместных событий равна сумме относительных частот этих событий

Определение

Вероятностью события называется число (предел), около которого группируются значения частоты данного события в различных сериях большого числа испытаний (n→µ)

Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных могущих повторяться в неограниченное число раз условиях.

ВОПРОС № 6

Формула Бернулли. Локальная и интегральная теоремы Лапласса. Формула Пуассона. Статистическое определение вероятности

Пример

В определенной ситуации вероятность выигрыша на бирже в течении дня равна 0,3. Какие варианты событий возможны при биржевой игре в той же ситуации в течении двух дней

p=0,3 ; q=0,7

1) 0,3*0,3

2) 0,3*0,7

3) 0,7*0,3

4) 0,7*0,7

2 – биноминальный коэффициент, число C

Определение

Производятся испытания, каждом из которых может появиться событие A с вероятностью p или не появиться событие A ( 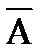) с вероятностью q. Если вероятность события A в одном испытании не зависит от появления его в любом другом, то испытания являются независимыми относительно события A. Будем считать, что испытания происходят в одинаковых условиях и вероятность появления события A в каждом испытании одна и та же.

Формула Бернулли

Вероятность того, что в серии из n испытаний (независимых) событие A появится ровно k раз и не появится n-k раз равна:

P_n(k)=C^k_n*p^k*q^n-k

Пример

p=0,9 q=0,1; n=4; k=3

P₄(3)=C³₄*0,9³*0,1=0,2916

Формула Бернулли применима к небольшим числам.

Теорема Пуассона

Если вероятность P наступления события A в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность того, что событие A наступит ровно k раз приближенно равна:

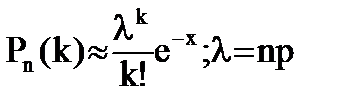
При npq≥10, то применяют формулы Лапласса, если npq<10, то формулы Пуассона.

Пример

Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что при транспортировке будет повреждено не более 3х изделий?

ВОПРОС № 7

ВОПРОС № 8

Функция и плотность распределения непрерывной случайной величины. Числовые характеристики непрерывной случайной величины.

Теорема

Вероятность того, что случайная величина примет значение в интервале (a;b) Ì [a;b] равна разности значений её функции распределения на концах этого интервала: P(a<X<b)= F(b)-F(a)

О. Плотностью распределения вероятностей непрерывной случайной величины X называется производная её функции распределения вероятностей f(x)=F’(x).

Если известна плотность распределения, то функцию распределения можно найти по формуле:

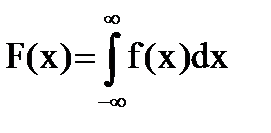
Свойства плотности распределения:

1) Плотность распределения – неотрицательная функция

2) Интеграл по бесконечному промежутку от плотности распределения вероятности равен 1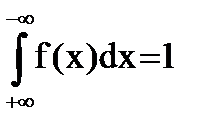

Следствие:

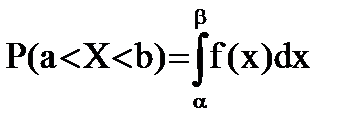
Пример:Плотность распределения вероятности имеет вид:

Рис1

ВОПРОС № 9.

ВОПРОС № 10

Равномерное распределение

Равномерное распределение применяется при анализе времени ожидания, при точно-периодическом через каждые t единиц времени прибытии обслуживающего устройства и при случайном поступлении заявки на обслуживание в этом интервале.

О. Равномерно распределенная на отрезка [a;b] случайная величина имеет плотность распределение

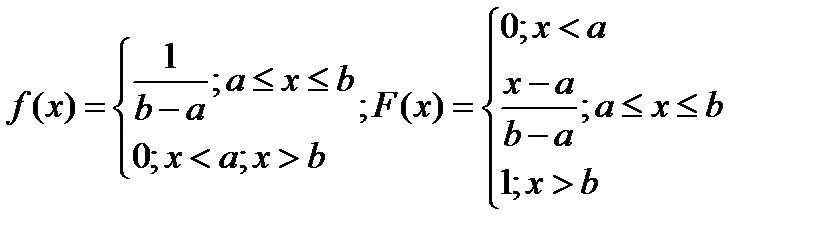
Вероятность того, что случайная величина попадет в промежуток (α<X<β), равна:

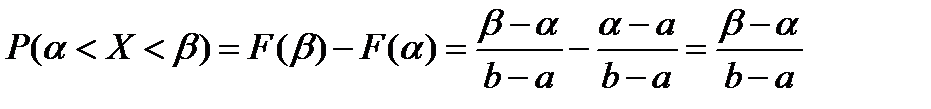
Показательное распределение. Показательное ( экспоненциальное ) распределение описывает случайные величины характеризующие длительность жизни, элементов, систем индивидуума ( задачи теории надежности, демографии и др.)

Опр. Распределение непрерывной случайной величины Х называется показательным если плотность распределения имеет вид:

f(x)= Система: 0, х<0; Л е^ -Лх, Х>=0

Вероятность попаданий случайной величины Х от а А до В равна е^-Ла – е^-Лв

Р(а<X<в) = е^-Ла – е^-Лв

F(в)- F(a)= 1– е^-Лв – (1- е^-Ла)

Математическое ожидание, дисперсия и среднеквадратическое отклонение показательного распределения соответственно равны:

М(х)= 1/Л

ВОПРОС № 11

ВОПРОС № 12. Коэффициент корреляции. Уравнение линейной регрессии

Коэффициент корреляции случайных величин называют величину «ро»

Рху = на листочке

Зависимость между случайными величинами Х и У характеризуемая коэффициентом корреляцией называется корреляцией. Случайной величиной (СВ) ХУ называются некоррелированными если «ро» ху = 0, что равносильно (сигма ху = 0)

Если «ро» ху не равно нулю, то СВ ху называют коррелируемыми.

Св-ва коэф. Корреляции: ( на листочке)

Если Х и У независимы СВ, то ХУ – некоррелированные, обратное утверждение неверно.

Уравнение линейной регрессии: У=а+вх

ВОПРОС № 13

ВОПРОС № 14.

Генеральная совокупность и выборка. Вариационный ряд. Гистограмма и полигон частот. Эмпирическая функция распределения.

Генеральной совокупностью называют совокупность объектов из которых производится выборкой.

Выборкой называют совокупность случайно отобранных объектов.

Если выборка правильно отражает соотношение в генеральной совокупности то ее называют репрезентативной ( представительной)

Объемом совокупности называют число ее объектов. Выборка представляет собой ряд чисел являющимися характеристиками исследуемых объектов. Вариационный ряд Х*₁ Х*₂ ….Х*_n представляет собой ту же самую выборку но расположены в порядке неубывания элементов:

Х*₁ <= Х*₂ <=…<= Х*_n

Значение случайной величины соответствующие отдельной группе сгруппированного ряда наблюдаемых данных называется вариантой (Хi)

Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой вариантой (ni)

Σ_ni =n

Отношение частоты данной варианты к объему выборки называется относительной частотой данной варианты. Р*_i = n_i/n

Дискретным вариационным рядом называется ранжированная ( в порядке неубывания) совокупность вариант X_i c соответствующим им частотами или относительными частотами.

Интервальным вариационным рядом называется упорядоченная последовательность интервалов варьирования случайной величины с соответствующими частотами или относительными частотами попаданий в каждой из них значений случайной величины. Для наглядности наблюдаемые данные изображают графически. Интервальный вариационный ряд графически изображается с помощью гистограммы. Для ее построения в прямоугольной системе координат на оси Х откладываются интервалы варьирования, а на оси У частоты или относительной частоты.

Вариационный ряд дискретной случайной величины графически представляет в виде полигона распределение частот или относительных частот, для этого в прямоугольной системе координат строятся точки с координатами (Хi; ni) затем последовательно соединяются ломанными линиями, которые называются полигонами.

Эмпирическая функция распределения случайной величины Х называют функцию относительной частоты числа наблюдений n_х

F*(x)=n_x/n, где n_x/n – относительная частота события где Х<х. Эта функция служит для приближенного представления о теоретической функции распределения. График эмпирической функции называют графиком накопленных частот.

Функция дискретной случайной величины. Начальные моменты. Основные распределения дискретной случайной величины.

О. Функция распределения для дискретной случайной величины X, которая может принимать значения x1, x2 … xn с соответствующими вероятностями имеет вид:

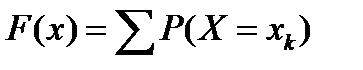
Суммируются вероятности тех значений, которые меньше x.

Пример

X
P	0,2	0,4	0,3	0,1

Дискретная случайная величина x делит бесконечную прямую на промежутки:

X	(-∞;0]	(0;1]	(1;2]	(2;3]	(3;+∞]
P		0,2	0,6	0,9

Начальные и центральные моменты

Начальные и центральным момента k случайной величины X считается математическое ожидание величины X в степени k:

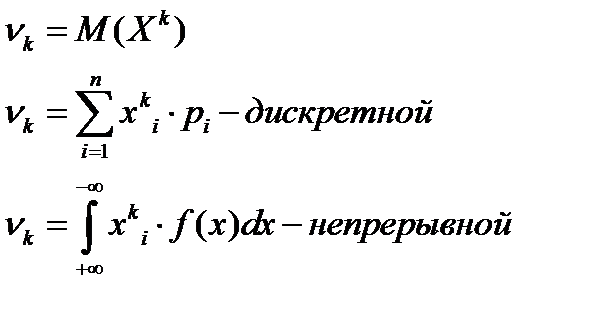
Начальный момент равен математическому ожиданию случайной величины X V1=M(X)

Центральным моментом порядка k случайной величины X называется математическое ожидание величины (X-M(X))^k и обозначается: μ_k=(X-M(X))^k

Следствия:

1. Центральный момент первого порядка равен нулю:

μ₁=(X-M(X))¹=M(X)-M(M(X))=M(X)-M(X)=0

2. Центральный момент второго порядка равен дисперсии:

μ₂=(X-M(X))²=D(X)

D(X)=M(X²)-(M(X))²=ν₂-ν₁²

Характеристики формы распределения:

Одно из характеристик служит коэфициет ассиметрии β₁:

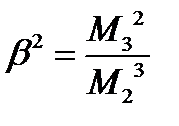
Локальная теорема Лапласа

При больших n вероятность того, что из n независимых испытаний событие A произойдет ровно k раз приближенно равна:

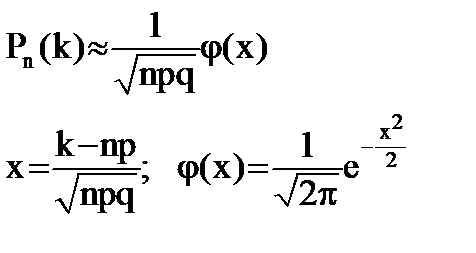
Пример:

Монету бросают 100 раз. Какова вероятность того, что при этом герб выпадет ровно 50 раз?

Hbc1

ВОПРОС № 1

Предмет теории вероятности. Пространство элементарных событий. Алгебра событий

По форме проявления причинных связей, законы природы и общества делятся на 2 класса: детерминированные (подчиняющиеся определенным законам) и статистические (явления, результаты которых мы предсказать не можем). К статистическим явлениям применяют слово «вероятно».

Теория вероятности – это математическая наука, изучающая закономерности случайных явлений. Например, модель роста числа жителей даёт теория вероятности, а конкретные данные – это статистика.

На теорию вероятностей опирается математическая статистика, задача которой состоит в том, чтобы по ограниченным данным восстановить с определенной степенью достоверности характеристики, присущие генеральной совокупности (т.е. всему мыслимому набору данных, описывающему изучаемое явление).

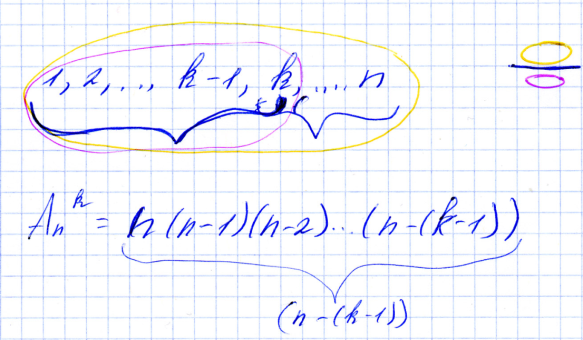
Определение

Событие называетсяслучайнымв данном опыте, если оно может произойти, а может и не произойти в этом опыте.

Все возможные в данном опыте исходы составляют множество Ω, которое называется пространством элементарных исходовили элементарных событий.

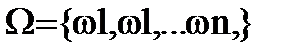
О. Событие– это произвольный набор элементарных исходов, или произвольное подмножество множества элементарных исходов Ω.

События обозначают латинскими буквами A, B, H… Для наглядности события изображают на диаграмме Венна. Геометрически она совершенно не верна, но удобна для демонстрации множеств.

О. Событие, происходящее всегда ( при любом элементарном исходе ) называется достоверным и обозначается Ω.

О. Невозможноесобытие не происходит никогда (не содержит ни одного элементарного исхода). Обозначается как пустое множество .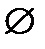

Действия над событиями

О. Пересечение (произведение) двух событий A и B называется событие C, происходящее тогда и только тогда, когда наступают одновременно 2 события A и B (состоящее из тех элементарных исходов, которые принадлежат и A, и B).

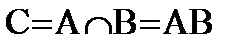
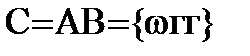
О. 2 события называются совместными, если они пересекаются.

О. 2 события называются несовместными, если они не пересекаются.

Два события называются противоположными, если появление одного из них равносильно непоявлению другого.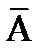

О. Объединением (суммой) 2х событий A и B называется событие C, происходящее тогда и только тогда, когда наступает хотя бы одно из событий A или B (состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из множеств.

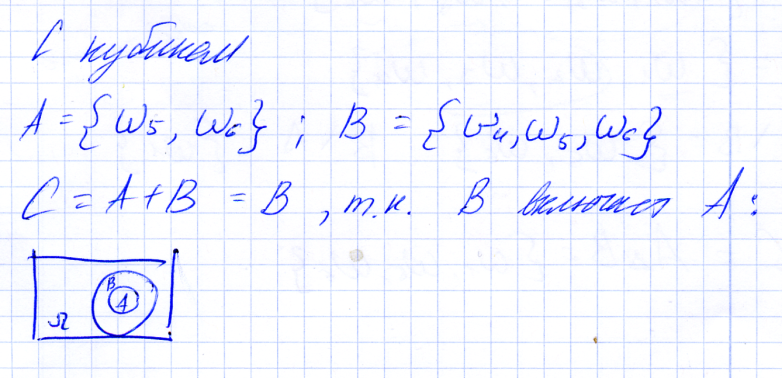
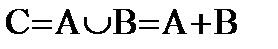
Сумма событий вовсе не означает сложение исходов!

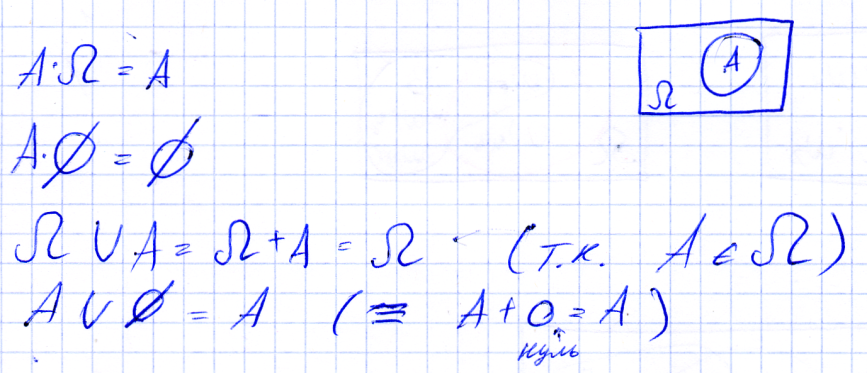
О. Разностью двух событий A и B называется событие C, происходящее тогда и только тогда, когда происходит событие A, но не происходит событие B (состоящее из тех элементарных исходов, которые принадлежат A, но не принадлежат B.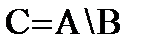

О. Симметрической разностью двух событий A и B называется событие C, представляющее объединение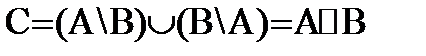

Пример

А: «Выпадение не менее 2х очков при бросании кубика». B: «Выпадение не более 4х очков» Найти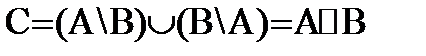

ДЗ:

Пользуясь диаграммой Венна, показать справедливость формул де Моргана.

О. 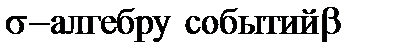можно определить как систему подмножеств пространства элементарных исходов Ω, замкнутую относительно счётного числа теоретико-множественных операций.

О. Множество событий A1, A2,…An называют полной группой событий, если они попарно несовместны и появление одного и только одного из них является достоверным событием.

ВОПРОС № 2

Элементы комбинаторики. Понятие случайного события. Классическое определение вероятности.

Комбинаторика изучает способы подсчёта числа элементов в различных конечных множествах.

Пример

ШПС

ШСП

ПШС

ПСШ

СШП

СПШ

Определение

Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Обозначаются перестановки P_n. P₃=6

Теорема

Число перестановок множества из n-ных элементов равно:

P_n=n! (факториал – произведение всех натуральных чисел начиная с единицы)

P_n=1∙2∙3∙…∙n

Пример:

1,2,3,4 Сколько можно составить двузначных чисел

12 13 14 21 23 24 31 32 34 41 42 43

Ответ: 12

Размещениями называют множества, выбранные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком.

Обозначение:

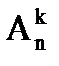
Число размещений из n элементов по k равно:

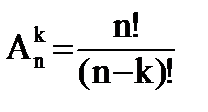
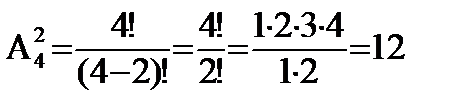
В хоккейном турнире участвуют 6 команд. Каждая команда должна сыграть с каждой 1 игру. Сколько игр сыгранно в турнире?

Определение

Сочетаниями из n различных элементов по k называются множества, которые отличаются хотя бы одним элементом. Обозначаются сочетания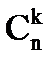

Теорема

Число сочетаний из n по k:

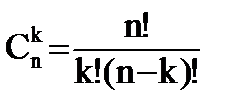
По определению 0!=1. Факториал относится к натуральным числам, поэтому считается, чо упорядочить 0 объектов можно единственным образом.

При решении задач комбинаторики используются следующие правила:

1. Правило суммы: если некоторый объект A может быть выбран из множества объектов m-способами, а другой объект B может быть выбран n-способами, то выбрать либо A, либо B можно m+n способами («или» это +)

2. Правило произведения: если некоторый объект A может быть выбран из множества объектов m-способами, и после каждого такого выбора объект B может быть выбран n-способами, то пара объектов AB в указанном порядке может быть выбрана m∙n способами («и» это ∙)

Принцип математической индукции –

Утверждение P(k) зависящее от натурального числа k справедливо при любом k из N, если утверждение P(k) справедливо при k=1

Для всякого l из N из справедливости P(l) следует справедливость P(l+1).

Лемма 1

Каково бы ни было целое число n≥1, число различных размещений по одному объекту из заданных n равно:

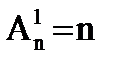
У нас n объектов. Мы можем выбрать каждый объект только одним способом.

Число 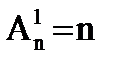есть суммарное число различных способов, какими один объект может быть выбран из n объектов. Выбранным может быть либо первый, либо второй, либо третий …. либо n-ый:

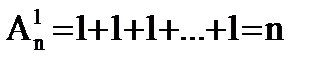
Лемма 2

Каковы бы ни были n≥2, 1<k≤n, число различных размещений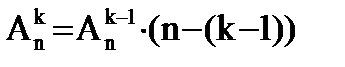

Доказательство:

1,2,3,…k-1,k,…n

Пусть имеется размещение k-1 объектов из n объектов. В этом размещении имеется (k-1) упорядоченно размещенных объектов и (n-(k-1)) оставшихся неразмещенных объектов. На следующую k-тую позицию можно выбрать любой из оставшихся неупорядоченных объектов. Таким образом, каждому конкретному размещению (k-1) объектов из n можно поставить в соответствие (n-(k-1)) размещений k объектов из n. Это означает что A из n по k должно быть больше чем A из n по k-1 в (n-(k-1)) раз.

Теорема

Каковы бы ни были числа 1≤k≤n, число размещений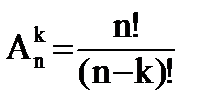

По второй лемме:

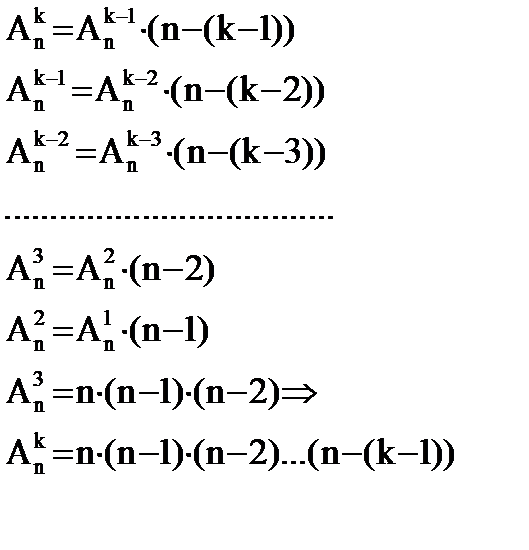
Определение

Событие называетсяслучайнымв данном опыте, если оно может произойти, а может и не произойти в этом опыте.

Все возможные в данном опыте исходы составляют множество Ω, которое называется пространством элементарных исходовили элементарных событий.

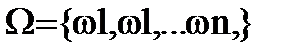
О. Событие– это произвольный набор элементарных исходов, или произвольное подмножество множества элементарных исходов Ω.

События обозначают латинскими буквами A, B, H… Для наглядности события изображают на диаграмме Венна. Геометрически она совершенно не верна, но удобна для демонстрации множеств.