Исследование системы линейных уравнений.

Вопрос №1

Матрицы и многомерные векторы. Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше) главной диагонали равны 0, то она называется верхний(нижний) треугольник.

Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться транспонированной к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Вопрос №3

Перестановки. Расположение n элементов набора в произвольном порядке называется перестановка.Транспозицией называется перестановка двух каких либо элементов. Инверсией в перестановке называется наличие пары чисел, в которое большее число предшествует меньшему. Если число инверсий в перестановке честное, то она называется четной и наоборот.

Определитель произвольного порядка. Определителем квадратной матрицы n-го порядка, называется число равное алгебраической сумме n факториал слагаемых, каждый из которых является произведением n элементов матрицы взятых по одному из каждой строки и столбца, при этом каждое слагаемое умножается на (-1) в степени число инверсий в перестановке j если первые индексы взяты в порядке нарастания.

Вопрос №2

Определители 2-го и 3-го порядка и их свойства. Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае - матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка, называется число равное разности произведений элементов главной и побочной диагонали матрицы.

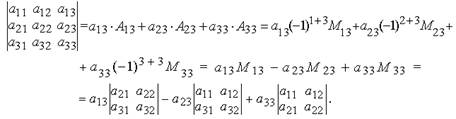Определителем квадратной матрицы 3-го порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не меняется.

4) При перестановки, каких либо двух строк (столбцов) матрицы знак матрицы меняется на противоположный. Доказательство вытекает из того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки (столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая k-строка (столбец) в первом определителе содержит первые слагаемые, во втором вторые.

8) Определитель матрицы не изменится если к элементам какой либо строки (столбца) прибавить элемент какой либо строки (столбца) предварительно умноженные на одно и то же число.

Вопрос №4

Миноры и алгебраические дополнения. Минором элемента a_ij квадратной матрицы |A| n-ного порядка, называется определителем матрицы, полученной из матрицы |A| вычеркиванием i-той строки j-того столбца.

Алгебраическим дополнением A_ij элемента a_ij квадратной матрицы |A|, называется минор этого элемента, умноженный на (-1) в степени.

Вычисление определителей произвольного порядка (теорема Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: 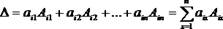(разложение по элементам i-й строки); 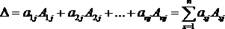(разложение по элементам j-го столбца).

Вопрос №6

Системы линейных уравнений. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

- система линейных уравнений.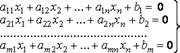

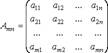Обозначим, - матрица коэффициентов, - вектор неизвестных,

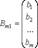- вектор свободных членов. A_mn X_n1 + B_m1 = 0 - матричная запись системы уравнений.

Если система уравнений имеет решение, она называется совместной, не имеет – несовместной. Совместная система, имеющая одно решение, называется определенной, если много – неопределенной. Две системы уравнений называются равносильными или эквивалентными, если каждое решение является решением уравнения системы или наоборот.

Вопрос №8

Решение систем линейных уравнений с помощью определителей (формулы Крамера). Пусть Δ = |A| определитель матричной системы n линейных уравнений с n неизвестных, а Δ_j определитель матрицы, полученный из матричной системы заменой j-того столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет единственное решение, определенное по формулам x_j = Δ_j / Δ (j = 1,2,…n) – формула Крамера.

Вопрос №7

Обратная матрица. Матрицей, обратной матрице А, называется матрица A^-1 такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие является и достаточным для существования A^-1 матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1 существует.

2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i - ой строки и j - го столбца будет алгебраическое дополнение A_ij элемента a_ij исходной матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для квадратной матрицы А существует и при том единственная обратная матрица А^-1 тогда и только тогда, когда эта матрица не вырождена.

Решение систем линейных уравнений с помощью обратной матрицы. Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из этих условий следует, что 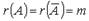и, следовательно, система совместна и определена. Решение системы можно получить так: 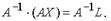. Используя свойства произведения матриц и свойство обратной матрицы 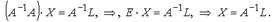. Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.

Пример. Решить систему 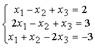матричным методом. Решение. Найдем обратную матрицу для матрицы коэффициентов системы .

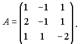Вычислим определитель, раскладывая по первой строке: 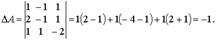. Поскольку Δ ≠ 0, то A^-1 существует.

Обратная матрица найдена верно.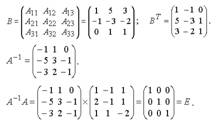

Найдем решение системы .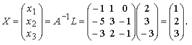

Следовательно, x₁ = 1, x₂ = 2, x₃ = 3.

Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.

Вопрос №10

Теорема Кронекера-Капелли. Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

Вопрос №9

Решение и исследование систем линейных уравнений методом Гаусса. Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно - предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:

- перестановка местами двух уравнений;

- умножение обеих частей одного из уравнений на любое число, отличное от нуля;

- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.

Вопрос №11

Базис и размерность пространства решений однородной системы линейных уравнений. Базисом линейного пространства L называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов. В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

В линейном пространстве любые два базиса содержат одинаковое число векторов.

Линейное пространство L, в котором существует базис, состоящий из n векторов, называется - n мерным линейным или векторным пространством. Число n называется размерностью пространства и обозначается dimL. Линейное пространство, в котором не существует базис, называется бесконечномерным.

Общее решение неоднородной системы линейных уравнений. Систему неоднородных уравнений запишем в матричном виде Ax = b, где матрица A имеет размеры mxn.

[T] Система линейных уравнений Ax = b может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.

[D] Пусть система имеет решение x⁽⁰⁾ . Если однородная система Ax = 0 имеет только одно решение, то из формулы общего решения будет следовать, что x⁽⁰⁾ - единственное решение неоднородной системы. Если однородная система имеет хотя бы одно ненулевое решение, то ее фундаментальная система решений будет состоять не менее, чем из одного решения. В формуле общего решения неоднородной системы будет произвольный коэффициент С1 , и при различных его значениях мы будем получать различные решения неоднородной системы.

Вопрос №12

Векторы на плоскости и в пространстве. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Ортом вектора а называется вектор а⁰, который имеет единичную длину и то же направление, что и вектор а.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Три вектора, a,b,c, называются линейно-независимыми, если они не лежат в одной плоскости.

Базисом в трехмерном пространстве R³ называется упорядоченная тройка любых линейно-независимых векторов.

Векторы и линейные операции над ними. Линейными операциями над векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

Разностью векторов a и b называют вектор a+(-b). Второе слагаемое является вектором, противоположным вектору b по направлению, но равным ему по длине.

Длина вектора. Длиной (модулем) вектора называется расстояние между началом и концом вектора.

Вопрос №13

Координаты на прямой. Упорядоченная тройка некомпланарных векторов e₁, e₂, e₃ называется базисом в множестве всех геометрических векторов. Всякий геометрический вектор a может быть единственным образом представлен в виде a=x₁e₁+x₂e₂+x₃e₃ числа x₁ , x_{2 ,} x₃ называют координатами вектора а в базисе (e₁, e₂, e₃).

Деление отрезка в данном отношении 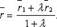. В координатах:

на прямой 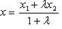; на плоскости 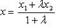, 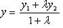; в пространстве , , .

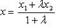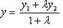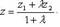Вопрос №17

Вопрос №19

Вопрос №20

Вопрос №21

Вопрос №22

Прямая на плоскости. Через две точки проходит единственная прямая и через точку, лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной

Вопрос №23

Угол между прямыми на плоскости. Условие параллельности и перпендикулярности прямых. Определение. Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как 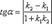. Две прямые параллельны, если k₁ = k₂. Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Вопрос №24

Вопрос №25

Вопрос №28

Вопрос №29

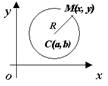Окружность. Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности.

Пусть центр окружности находится в точке С(а, b). Т.к. окружность есть множество точек М(х, у), находящихся на расстоянии R (радиус окружности) от центра С(а, b), то 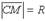, то есть 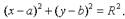(1). Уравнение (1) и есть уравнение окружности с центром в точке С(а, b) и радиусом R. Если центр окружности находится в начале координат, то ее уравнение примет вид: .

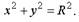Эллипс. Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

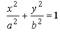- каноническое уравнение эллипса.

Форма. Из канонического уравнения понятно, что оси координат Ох и Оу являются осями симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса.

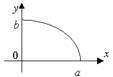Рассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать каноническоеуравнение в виде: .

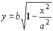Отсюда видно, что если x = 0, то y = b и, далее, с ростом х значения у убывают. Когда x = a, то y = 0.

Числа а и b называют полуосями эллипса.

Учитывая симметрию эллипса относительно осей координат, можем построить полный эллипс.

Если изменяется величина с, то меняется форма эллипса, а именно: если 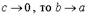и при c = 0 эллипс становится окружностью с уравнением 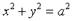. Т.о., окружность есть частный случай эллипса, когда полуоси эллипса равны между собой.

Если же с->a, то 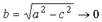, т.е. эллипс сжимается вдоль оси Оу. Величина c\a может служить числовой характеристикой сжатия эллипса.

Число 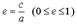называют эксцентриситетом эллипса. Две прямые 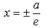называются директрисами эллипса. Точки пересечения эллипса с осями симметрии называют вершинами эллипса.

Вопрос №30

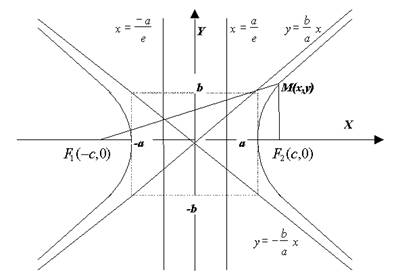
Гипербола есть геометрическое место точек, абсолютное значение разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами.

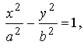- каноническое уравнениегиперболы.

Число а называют действительной полуосью Число а называют действительной полуосью гиперболы, число b - мнимой полуосью.

Кривая состоит из двух отдельных частей - ветвей гиперболы, лежащих в областях .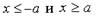

Можно показать, что при 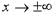ветви гиперболы неограниченно приближаются к прямым 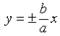, не пересекая этих прямых.

Эти две прямые называются асимптотами гиперболы.

Число 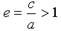, количественно характеризующее сжатие ветвей гиперболы, называют эксцентриситетом гиперболы.

Точки пересечения гиперболы с действительной осью называются вершинами гиперболы.

Две прямые 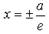называют директрисами гиперболы.

Директрисы гиперболы параллельны оси Оу и пересекают ось Ох между вершинами гиперболы.

Вопрос №31

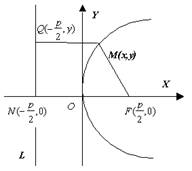Парабола есть геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой (директриса не проходит через фокус).

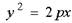- каноническое уравнение параболы.

Значение р называют параметром параболы.

Вопрос №1

Матрицы и многомерные векторы. Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше) главной диагонали равны 0, то она называется верхний(нижний) треугольник.

Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться транспонированной к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Вопрос №3

Перестановки. Расположение n элементов набора в произвольном порядке называется перестановка.Транспозицией называется перестановка двух каких либо элементов. Инверсией в перестановке называется наличие пары чисел, в которое большее число предшествует меньшему. Если число инверсий в перестановке честное, то она называется четной и наоборот.

Определитель произвольного порядка. Определителем квадратной матрицы n-го порядка, называется число равное алгебраической сумме n факториал слагаемых, каждый из которых является произведением n элементов матрицы взятых по одному из каждой строки и столбца, при этом каждое слагаемое умножается на (-1) в степени число инверсий в перестановке j если первые индексы взяты в порядке нарастания.

Вопрос №2

Определители 2-го и 3-го порядка и их свойства. Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае - матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка, называется число равное разности произведений элементов главной и побочной диагонали матрицы.

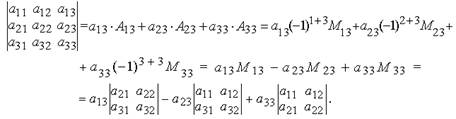Определителем квадратной матрицы 3-го порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не меняется.

4) При перестановки, каких либо двух строк (столбцов) матрицы знак матрицы меняется на противоположный. Доказательство вытекает из того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки (столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая k-строка (столбец) в первом определителе содержит первые слагаемые, во втором вторые.

8) Определитель матрицы не изменится если к элементам какой либо строки (столбца) прибавить элемент какой либо строки (столбца) предварительно умноженные на одно и то же число.

Вопрос №4

Миноры и алгебраические дополнения. Минором элемента a_ij квадратной матрицы |A| n-ного порядка, называется определителем матрицы, полученной из матрицы |A| вычеркиванием i-той строки j-того столбца.

Алгебраическим дополнением A_ij элемента a_ij квадратной матрицы |A|, называется минор этого элемента, умноженный на (-1) в степени.

Вычисление определителей произвольного порядка (теорема Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: 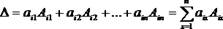(разложение по элементам i-й строки); 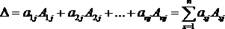(разложение по элементам j-го столбца).

Вопрос №6

Системы линейных уравнений. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

- система линейных уравнений.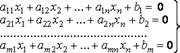

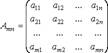Обозначим, - матрица коэффициентов, - вектор неизвестных,

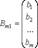- вектор свободных членов. A_mn X_n1 + B_m1 = 0 - матричная запись системы уравнений.

Если система уравнений имеет решение, она называется совместной, не имеет – несовместной. Совместная система, имеющая одно решение, называется определенной, если много – неопределенной. Две системы уравнений называются равносильными или эквивалентными, если каждое решение является решением уравнения системы или наоборот.

Вопрос №8

Решение систем линейных уравнений с помощью определителей (формулы Крамера). Пусть Δ = |A| определитель матричной системы n линейных уравнений с n неизвестных, а Δ_j определитель матрицы, полученный из матричной системы заменой j-того столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет единственное решение, определенное по формулам x_j = Δ_j / Δ (j = 1,2,…n) – формула Крамера.

Вопрос №7

Обратная матрица. Матрицей, обратной матрице А, называется матрица A^-1 такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие является и достаточным для существования A^-1 матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1 существует.

2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i - ой строки и j - го столбца будет алгебраическое дополнение A_ij элемента a_ij исходной матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для квадратной матрицы А существует и при том единственная обратная матрица А^-1 тогда и только тогда, когда эта матрица не вырождена.

Решение систем линейных уравнений с помощью обратной матрицы. Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из этих условий следует, что 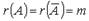и, следовательно, система совместна и определена. Решение системы можно получить так: 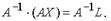. Используя свойства произведения матриц и свойство обратной матрицы 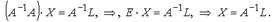. Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.

Пример. Решить систему 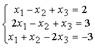матричным методом. Решение. Найдем обратную матрицу для матрицы коэффициентов системы .

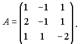Вычислим определитель, раскладывая по первой строке: 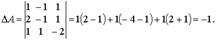. Поскольку Δ ≠ 0, то A^-1 существует.

Обратная матрица найдена верно.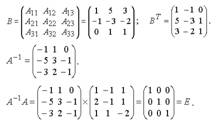

Найдем решение системы .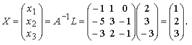

Следовательно, x₁ = 1, x₂ = 2, x₃ = 3.

Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.

Вопрос №10

Теорема Кронекера-Капелли. Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

Исследование системы линейных уравнений.

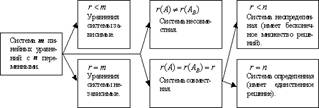
Вопрос №9

Решение и исследование систем линейных уравнений методом Гаусса. Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно - предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:

- перестановка местами двух уравнений;

- умножение обеих частей одного из уравнений на любое число, отличное от нуля;

- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.

Вопрос №11

Базис и размерность пространства решений однородной системы линейных уравнений. Базисом линейного пространства L называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов. В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

В линейном пространстве любые два базиса содержат одинаковое число векторов.

Линейное пространство L, в котором существует базис, состоящий из n векторов, называется - n мерным линейным или векторным пространством. Число n называется размерностью пространства и обозначается dimL. Линейное пространство, в котором не существует базис, называется бесконечномерным.

Общее решение неоднородной системы линейных уравнений. Систему неоднородных уравнений запишем в матричном виде Ax = b, где матрица A имеет размеры mxn.

[T] Система линейных уравнений Ax = b может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.

[D] Пусть система имеет решение x⁽⁰⁾ . Если однородная система Ax = 0 имеет только одно решение, то из формулы общего решения будет следовать, что x⁽⁰⁾ - единственное решение неоднородной системы. Если однородная система имеет хотя бы одно ненулевое решение, то ее фундаментальная система решений будет состоять не менее, чем из одного решения. В формуле общего решения неоднородной системы будет произвольный коэффициент С1 , и при различных его значениях мы будем получать различные решения неоднородной системы.

Вопрос №12

Векторы на плоскости и в пространстве. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Ортом вектора а называется вектор а⁰, который имеет единичную длину и то же направление, что и вектор а.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Три вектора, a,b,c, называются линейно-независимыми, если они не лежат в одной плоскости.

Базисом в трехмерном пространстве R³ называется упорядоченная тройка любых линейно-независимых векторов.

Векторы и линейные операции над ними. Линейными операциями над векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместит