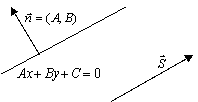Геометрический смысл модуля действительного числа
Вопрос.
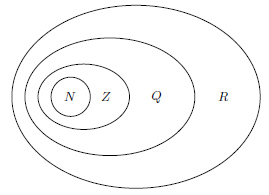
· Числа вида N = {1, 2, 3, ....} называются натуральными. Натуральные числа появились в связи с необходимостью подсчета предметов.
· Числа вида: Z = {... -3, -2, -1, 0, 1, 2, 3, ....} называются целыми числами, т.е. целые числа - это натуральные числа, числа, противоположные натуральным, и число 0.
· Целые и дробные числа составляют множество рациональных чисел: Q = Z  {n/m}, где m -целое число, а n -натуральное число.
{n/m}, где m -целое число, а n -натуральное число.
· Вместе оба множества — рациональных и иррациональных чисел — образуют множество действительных (или вещественных) чисел, которое обозначается R
Вопрос.
· Десятичная дробь — это любая числовая дробь, в знаменателе которой стоит степень десятки.
· Существуют знаменатели, которые не приводятся к степени десятки.
· Если в разложении на простые множители присутствуют только множители 2 и 5, это число можно привести к степени десятки. Если найдутся другие числа (3, 7, 11 — что угодно), о степени десятки можно забыть.
· весь алгоритм перехода к десятичным дробям:
1. Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;
2. Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.
3. Собственно, умножить числитель и знаменатель исходной дроби на этот множитель — получим искомое представление, т.е. в знаменателе будет стоять степень десятки.
· Разумеется, дополнительный множитель тоже будет разлагаться только на двойки и пятерки. При этом чтобы не усложнять себе жизнь, следует выбирать наименьший такой множитель из всех возможных.
· если в исходной дроби присутствует целая часть, обязательно переведите эту дробь в неправильную. И только затем применяйте описанный алгоритм.
· Пример:
Разложим на множители знаменатель первой дроби: 4 = 2 · 2 = 22.Следовательно, дробь представима в виде десятичной. В разложении присутствуют две двойки и ни одной пятерки, поэтому дополнительный множитель равен 52 = 25. С ним количество двоек и пятерок сравняется. Имеем:
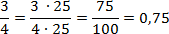
Теперь разберемся со второй дробью. Для этого заметим, что24 = 3 · 8 = 3 · 23 — в разложении присутствует тройка, поэтому дробь не представима в виде десятичной.
Две последних дроби имеют знаменатели 5 (простое число)и 20 = 4 · 5 = 22 · 5 соответственно — везде присутствуют только двойки и пятерки. При этом в первом случае «для полного счастья» не хватает множителя 2, а во втором — 5. Получаем:
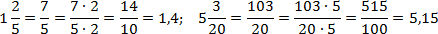
Вопрос.
1.Модуль действительного числа и его свойства.
В младших классах вы уже встречались с понятием модуля (или абсолютной величины) числа, пользовались обозначением | а |. Вы знаете, что, например, | 5 | = 5, | - 3 | = 3. Правда, раньше речь шла только о рациональных числах. Теперь надо
ввести понятие модуля для любого действительного числа.
Определение. Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.
Короче это записывают так:
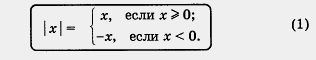
Например,
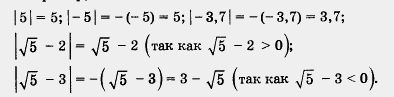
На практике используют различные свойства модулей, например:
1. |а| 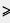 0.
0.
2.|аb| =|a| |b|.
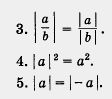
Вопрос.
Приближенные вычисления
Выполняя вычисления, всегда необходимо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают или не требуют этого (например, семизначная таблица логарифмов при вычислениях с числами, имеющими 5 верных значащих цифр - избыточна). Твёрдое знакомство с правилами приближенных вычислений необходимо каждому, кому приходится вычислять.
Погрешности
Разница между точным числом x и его приближенным значением a называется погрешностью данного приближенного числа. Если известно, что | x - a | < Da, то величина Da называется предельной абсолютной погрешностью приближенной величины a.
Отношение Da / a = da называется предельной относительной погрешностью; последнюю часто выражают в процентах.
Пример:
3,14 является приближенным значением числа p, погрешность его равна 0,00159..., предельную абсолютную погрешность можно считать равной 0,0016, а предельную относительную погрешность v равной 0.0016/3.14 = 0,00051 = 0,051%. Для краткости обычно слово ?предельная¦ опускается.
Значащие цифры
Если абсолютная погрешность величины a не превышает одной единицы разряда последней цифры числа a, то говорят, что у числа все знаки верные.
Приближенные числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52400 равна 100, то это число должно быть записано, например, в виде 524 .102или 0,524 .105. Оценить погрешность приближенного числа можно, указав, сколько верных значащих цифр оно содержит. При подсчете значащих цифр не считаются нули с левой стороны числа.
Примеры:
| 1 куб.фут = 0.0283 м3 - три верных значащих цифры 1 дюйм = 2,5400 v пять верных значащих цифр. |
Если число a имеет n верных значащих цифр, то его относительная погрешность da T 1/(z*dn-1), где z - первая значащая цифра числа a; d - основание системы счисления.
У числа a с относительной погрешностью da верны n значащих цифр, где n - наибольшее целое число, удовлетворяющее неравенству (1+Z)da T dl-n.
Пример:
Если число a = 47,542 получено в результате действий над приближенными числами и известно, что da = 0,1%, то a имеет 3 верных знака, так как (4+1)0,001 T 10v2.
Округление
Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры округленного числа. Поэтому, чтобы после округления все знаки были верны, погрешность до округления должна быть не больше половины единицы того разряда, до которого предполагают делать округление.
Действия над приближенными числами
Результат действий над приближёнными числами представляет собой также приближённое число. Погрешность результата может быть выражена через погрешности первоначальных данных при помощи следующих теорем:
Предельная абсолютная погрешность алгебраической суммы равна сумме предельных абсолютных погрешностей слагаемых.
Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых.
Относительная погрешность произведения или частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя.
Относительная погрешность n-ой степени приближенного числа в n раз больше относительной погрешности основания (как у целых, так и для дробных n).
Пользуясь этими теоремами, можно определить погрешность результата любой комбинации арифметических действий над приближенными числами.
Примеры:
V = r2h
Dv = Vd v = V(2d r+d n)
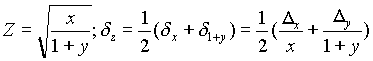
Предельная абсолютная погрешность заведомо превосходит абсолютную величину истинной погрешности, поскольку предельное значение вычисляется в предположения, что различные погрешности усиливают друг друга; практически это бывает редко. При массовых вычислениях, когда не учитывают погрешность каждого отдельного результата, пользуются следующими правилами подсчета цифр.
При соблюдении этих правил можно считать, что в среднем полученные результаты будут иметь все знаки верными, хотя в отдельных случаях возможна ошибка в несколько единиц последнего знака.
При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков.
При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр.
При возведении в квадрат или куб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближённое число ( последняя цифра квадрата и особенно куба при этом менее надежна, чем последняя цифра основания ).
При увеличении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их имеет приближённое значение подкоренного числа (последняя цифра квадратного и особенно кубического корня при этом более надёжна, чем последняя цифра подкоренного числа).
Во всех промежуточных результатах следует сохранять одной цифрой более, чем рекомендуют предыдущие правила. В окончательном результате эта ?запасная¦ цифра отбрасывается.
Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
Если данные можно брать с произвольной точностью, то для получения результата с K цифрами данные следует брать с таким числом цифр, какое даёт согласно правилам 1-4(К+1) цифру в результате.
Вопрос.
Определения. Матрицей называется прямоугольная таблица чисел или буквенных выражений, содержащая m строк и n столбцов: 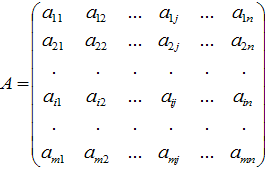 , , 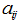 называют элементами матрицы. Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы: A = называют элементами матрицы. Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы: A = 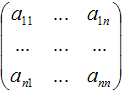 Элементы Элементы 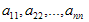 образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной. Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E . Если все элементы матрицы равны 0, то матрица называется нулевой и ее обозначают буквой O. Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной. Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E . Если все элементы матрицы равны 0, то матрица называется нулевой и ее обозначают буквой O. Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если 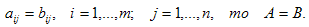 Сложение матриц. Суммой матриц Сложение матриц. Суммой матриц 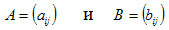 одной и той же размерности называется матрица размерности одной и той же размерности называется матрица размерности 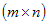 , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B: , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B: 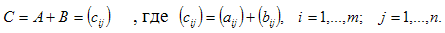 Матрицы разных размерностей складывать нельзя. Пример1. Матрицы разных размерностей складывать нельзя. Пример1. 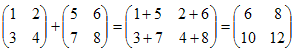 . Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность.(A+B)+C=A+(B+C) Умножение матриц, транспонирование матриц. Матрица C, элементы которой сij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α: . Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность.(A+B)+C=A+(B+C) Умножение матриц, транспонирование матриц. Матрица C, элементы которой сij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α: 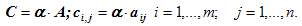 Пример 2. Пример 2. 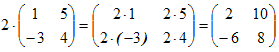 . Произведением матрицы . Произведением матрицы 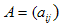 размерности размерности 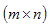 на матрицу на матрицу 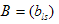 размерности размерности 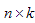 называется матрица называется матрица 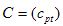 размерности размерности 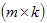 , где: , где: 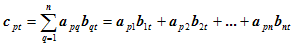 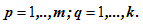 Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Пример 3. Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Пример 3. 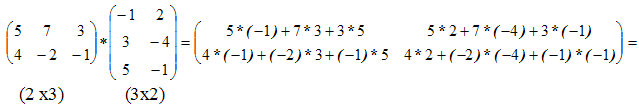 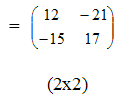 Пример 4. Пример 4. 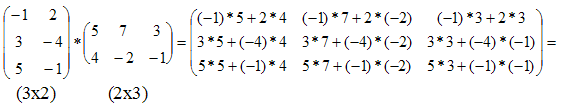 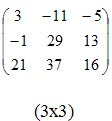 Результатом транспонирования матрицы Результатом транспонирования матрицы 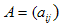 размерности размерности 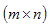 является матрица является матрица 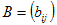 размерности размерности 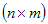 , где , где 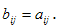 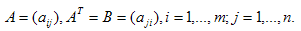 Пример 5. Пример 5.  Свойства транспонированных матриц. 1). Если E-единичная матрица, то E=ET. 2). Двукратное транспонирование не изменяет матрицу (AT)T=A. 3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)T=AT+BT 4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: Свойства транспонированных матриц. 1). Если E-единичная матрица, то E=ET. 2). Двукратное транспонирование не изменяет матрицу (AT)T=A. 3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)T=AT+BT 4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: 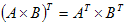 . 5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A-1)T=(AT)-1 . 6). Если транспонированная матрица AT совпадает с данной матрицей A, то матрица A называется симметрической. . 5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A-1)T=(AT)-1 . 6). Если транспонированная матрица AT совпадает с данной матрицей A, то матрица A называется симметрической. |
Вопрос.
Определения. Матрицей называется прямоугольная таблица чисел или буквенных выражений, содержащая m строк и n столбцов: 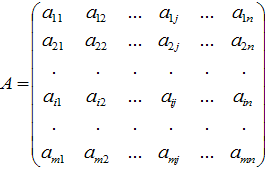 , , 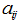 называют элементами матрицы. Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы: A = называют элементами матрицы. Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы: A = 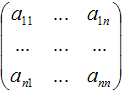 Элементы Элементы 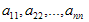 образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной. Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E . Если все элементы матрицы равны 0, то матрица называется нулевой и ее обозначают буквой O. Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной. Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E . Если все элементы матрицы равны 0, то матрица называется нулевой и ее обозначают буквой O. Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если 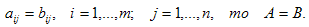 Сложение матриц. Суммой матриц Сложение матриц. Суммой матриц 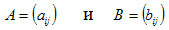 одной и той же размерности называется матрица размерности одной и той же размерности называется матрица размерности 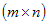 , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B: , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B: 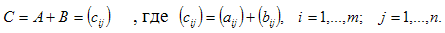 Матрицы разных размерностей складывать нельзя. Пример1. Матрицы разных размерностей складывать нельзя. Пример1. 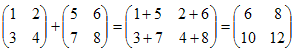 . Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность.(A+B)+C=A+(B+C) Умножение матриц, транспонирование матриц. Матрица C, элементы которой сij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α: . Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность.(A+B)+C=A+(B+C) Умножение матриц, транспонирование матриц. Матрица C, элементы которой сij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α: 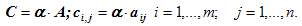 Пример 2. Пример 2. 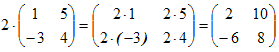 . Произведением матрицы . Произведением матрицы 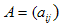 размерности размерности 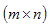 на матрицу на матрицу 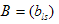 размерности размерности 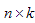 называется матрица называется матрица 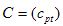 размерности размерности 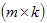 , где: , где: 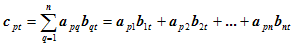 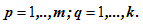 Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Пример 3. Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Пример 3. 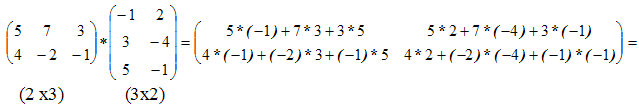 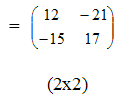 Пример 4. Пример 4. 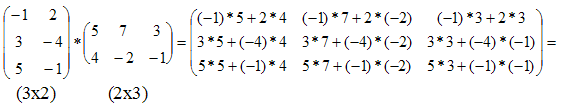 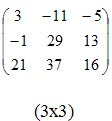 Результатом транспонирования матрицы Результатом транспонирования матрицы 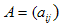 размерности размерности 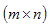 является матрица является матрица 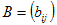 размерности размерности 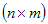 , где , где 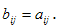 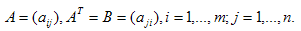 Пример 5. Пример 5.  Свойства транспонированных матриц. 1). Если E-единичная матрица, то E=ET. 2). Двукратное транспонирование не изменяет матрицу (AT)T=A. 3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)T=AT+BT 4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: Свойства транспонированных матриц. 1). Если E-единичная матрица, то E=ET. 2). Двукратное транспонирование не изменяет матрицу (AT)T=A. 3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)T=AT+BT 4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: 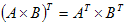 . 5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A-1)T=(AT)-1 . 6). Если транспонированная матрица AT совпадает с данной матрицей A, то матрица A называется симметрической. . 5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A-1)T=(AT)-1 . 6). Если транспонированная матрица AT совпадает с данной матрицей A, то матрица A называется симметрической. |
Вопрос.
Система линейных уравнений:
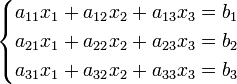
Определители:
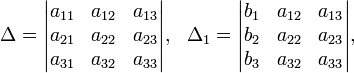
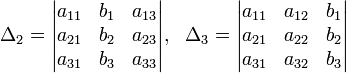
Решение:
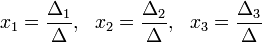
Пример:
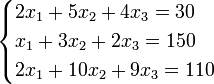
Определители:
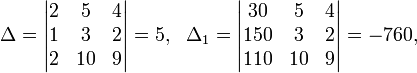
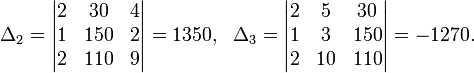
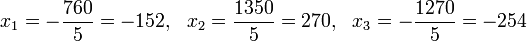
Вопрос.
Покажем, как методом Гаусса можно решить следующую систему:
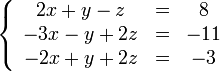
Обнулим коэффициенты при 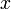 во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на
во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на 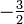 и
и 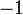 , соответственно:
, соответственно:
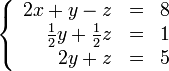
Теперь обнулим коэффициент при 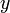 в третьей строке, вычтя из неё вторую строку, умноженную на
в третьей строке, вычтя из неё вторую строку, умноженную на 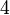 :
:
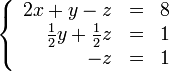
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
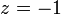 из третьего;
из третьего;
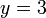 из второго, подставив полученное
из второго, подставив полученное 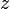
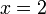 из первого, подставив полученные
из первого, подставив полученные 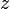 и
и 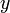 .
.
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
9-11 вопросы.
1. Основные формулы в декартовых прямоугольных координатах
При решении задач аналитической геометрии будем использовать действия над векторами, заданными в координатной форме.
Пусть даны векторы 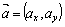 и
и 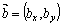 . Тогда:
. Тогда:
1) при сложении (вычитании) векторов 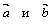 получим вектор
получим вектор 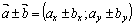 ;
;
2) при умножении вектора 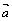 на число λ получим вектор
на число λ получим вектор 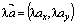 ;
;
3) при скалярном произведении векторов 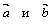 получим число
получим число 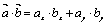 .
.
Расстояние между двумя точками
Даны точки А (xA, yA) и В (xВ, yВ). Расстояние между ними найдем, как длину вектора 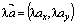 = (xВ – xА, yB - yA). Из скалярного произведения
= (xВ – xА, yB - yA). Из скалярного произведения 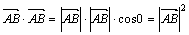 имеем
имеем 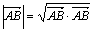 . Подсчитав скалярное произведение через координаты вектора
. Подсчитав скалярное произведение через координаты вектора 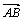 , получаем расстояние между двумя точками
, получаем расстояние между двумя точками
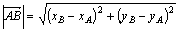 . (1)
. (1)
Угол между двумя векторами
Даны два вектора: 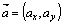 и
и 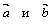 . Косинус угла между ними:
. Косинус угла между ними:
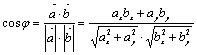 . (2)
. (2)
Деление отрезка в заданном отношении
Пусть даны точки А (xА y А), и В (xВ y В ). Требуется найти координаты точки С (x, y ) , делящей отрезок АВ в заданном отношении λ:
 В A С В A С | 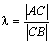 . . |
Для решения задачи воспользуемся действием умножения вектора на число. Перепишем отношение 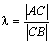 в виде: |AC|=λ| CB|. Такое соотношение длин может быть получено при выполнении действия
в виде: |AC|=λ| CB|. Такое соотношение длин может быть получено при выполнении действия 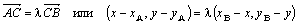 .
.
В равных векторах равны соответствующие координаты:
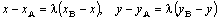 .
.
Из этих уравнений найдем неизвестные координаты точки С:
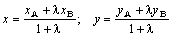 . (3)
. (3)
В частности, для середины имеем 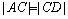 и поэтому λ=1. Следовательно, координаты середины отрезка находятся по формулам:
и поэтому λ=1. Следовательно, координаты середины отрезка находятся по формулам:
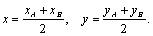 (4)
(4)
Условия параллельности и перпендикулярности векторов
Так как скалярное произведение двух перпендикулярных векторов 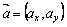 и
и 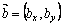 равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство
равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство 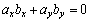 .
.
При умножении вектора 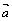 на скаляр
на скаляр 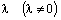 получаем вектор
получаем вектор 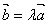 одного направления с
одного направления с 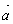 при λ > 0и противоположного направления при λ < 0. Но всегда векторы
при λ > 0и противоположного направления при λ < 0. Но всегда векторы 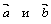 будут параллельны.
будут параллельны.
Поэтому условием параллельности векторов 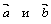 будет пропорциональность их соответствующих координат:
будет пропорциональность их соответствующих координат: 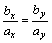 .
.
Пример. Найти длину медианы СЕ в треугольнике АВС с вершинами: А (3,3), В (–1,1), С (0,1).
Решение. Так как Е – середина отрезка АВ, то по формуле (4) имеем:
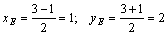 .
.
Длину медианы СЕ найдем по формуле (1):
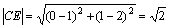 .
.
Пример. Какие из векторов 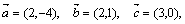
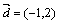 будут параллельны и какие перпендикулярны между собой?
будут параллельны и какие перпендикулярны между собой?
Решение. Векторы 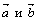 перпендикулярны, т.к.
перпендикулярны, т.к. 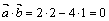 . Векторы
. Векторы 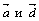 параллельны, т.к.
параллельны, т.к. 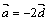 .
.
Пример. Найти геометрическое место точек, удаленных от точки А(а,b) на одно и тоже расстояние R.
Решение. Если М(х,у) – произвольная точка искомого геометрического места, то всегда |АМ|=R или 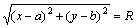 ,
,
(х-а)2 + (у-b)2 = R2 – искомое уравнение.
2. Линии и их уравнения
Понятия уравнения линии является дальнейшим развитием метода координат. Если точка в аналитической геометрии на плоскости определяется двумя числами (координатами точки), то линия определяется уравнением, связывающим координаты любой точки линии (уравнение линии). Составление уравнения линии заключается в алгебраической записи свойства, характеризующего эту линию как геометрическое место точек.
Точка пересечения двух линий, заданных уравнениями, может быть найдена путем решения системы, образованной из этих уравнений.
На примере уравнения окружности (х–а)2 + (у–b)2 = R2 видно, что кроме текущих координат х и у , уравнение может содержать еще и некоторые величины, остающиеся неизменными для данной фиксированной линии, но изменяющиеся при переходе к другой линии того же типа. В нашем примере это величины а, b и R, имеющие для каждой окружности свое значение. Такие величины называются параметрами, они определяют форму и размеры линии (например, параметр R в уравнении окружности), а также положение ее на плоскости относительно системы координат (как, например, координаты а и b центра окружности).
Пример. Найти уравнение линии, каждая точка которой равноудалена от прямой х = –2 и точки F (2,3).
Решение. Пусть М(х,у) – произвольная точка искомой линии.
Расстояние от точки М до прямой х = –2 есть длина перпендикуляра MN , опущенного из М на прямую. Определим координаты точки N . Очевидно, что абсцисса точки N равна –2, а ордината точки N равна ординате точки М, т.е. N (–2,у). По условию задачи | MN |=| MF |. Следовательно, для любой точки М(х,у), принадлежащей искомой линии, справедливо равенство:
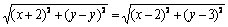 или или 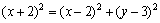 . Упростим полученное уравнение: . Упростим полученное уравнение: 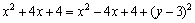 или или 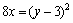 . Это и есть искомое уравнение. . Это и есть искомое уравнение. | N yM(x,y) 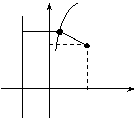 F (2,3) –2 0 2 x F (2,3) –2 0 2 x |
3. Уравнение прямой линии в пространстве R2: общее, каноническое уравнение прямой. Уравнение прямой с угловым коэффициентом
 В декартовой системе координат прямая представлена уравнением первой степени и, наоборот, всякое уравнение первой степениАх+Ву+С = 0 представляет некоторую прямую. Различные виды уравнения прямой (с угловым коэффициентом, каноническое и т.п.) являются частными случаями этого общего уравнения.
В декартовой системе координат прямая представлена уравнением первой степени и, наоборот, всякое уравнение первой степениАх+Ву+С = 0 представляет некоторую прямую. Различные виды уравнения прямой (с угловым коэффициентом, каноническое и т.п.) являются частными случаями этого общего уравнения.
Построим уравнение прямой, проходящей через точку М0(х0, у0) параллельно направляющему вектору 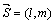 . Возьмем любую точку N(х,у), лежащую на заданной прямой. Вектор
. Возьмем любую точку N(х,у), лежащую на заданной прямой. Вектор 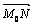 всегда будет параллелен вектору
всегда будет параллелен вектору 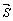 .
.
Условие параллельности векторов 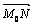 =(х-х0; у-у0) и
=(х-х0; у-у0) и 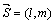 , дает каноническое уравнение прямой линии на плоскости:
, дает каноническое уравнение прямой линии на плоскости:
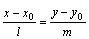 . (1)
. (1)
Введем вектор 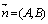 , перпендикулярный искомой прямой. Тогда из условия перпендикулярности векторов
, перпендикулярный искомой прямой. Тогда из условия перпендикулярности векторов 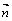 и
и 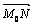 можно записать
можно записать 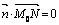 . В результате получаем уравнение: А(х-х0)+В(у-у0)=0 или
. В результате получаем уравнение: А(х-х0)+В(у-у0)=0 или
Ах+Ву+С=0, (2)
где С=–Ах0–Ву0.
| Уравнение (2) называется общим уравнением прямой на плоскости. Вектор 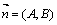 называется нормалью. Пример. Написать уравнение прямой, проходящей через точку Q(2, –3) параллельно оси Оу. называется нормалью. Пример. Написать уравнение прямой, проходящей через точку Q(2, –3) параллельно оси Оу. |
Решение. В качестве направляющего вектора 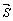 можно взять вектор
можно взять вектор 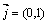 . Подставив данные в уравнении (1), получим:
. Подставив данные в уравнении (1), получим: 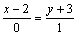 . Это каноническое уравнение обычно переписывают в общем виде: х–2=0 или х = 2.
. Это каноническое уравнение обычно переписывают в общем виде: х–2=0 или х = 2.
При 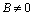 общее уравнение прямой (2) можно переписать в виде:
общее уравнение прямой (2) можно переписать в виде:
у=k x +b, (3)
где 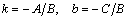 .
.
Уравнение (3) называется уравнением с угловым коэффициентом; угловой коэффициент k = tg α, где α – угол наклона прямой к оси Ох. При k=0 ( α= 0)уравнение (3) дает прямую, параллельную оси Ох. Из уравнения (3) нельзя получить уравнение прямой, параллельной оси Оу. Поэтому все семейство наклонных прямых (3) дополняется прямыми:
х=а, (4)
параллельными оси Оу. Уравнение (4) получено из уравнения (2) при В=0, где 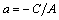 .
.
Уравнение прямой, проходящей через 2 точки
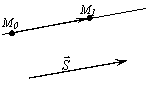 | Пусть даны точки М0(х0, у0) и М1(х1, у1). Требуется написать уравнение прямой, проходящей через эти точки. Для решения задачи воспользуемся уравнением (1). В качестве направляющего вектора 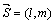 воспользуемся вектором воспользуемся вектором 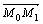 : : 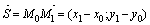 . . |
Подставим l =x 1– x0 и m= y1 –y0 в каноническое уравнение (1), получим уравнение прямой, проходящей через две точки:
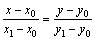 . (5)
. (5)
Уравнение прямой, проходящей через данную точку в заданном направлении
Пусть дана точка М0(х0, у0). Требуется написать уравнение прямой, проходящей через точку М0 в заданном направлении.
Задачу будем решать в зависимости от того, как определено направление прямой. Если направление задается вектором 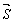 , то такая прямая описывается уравнением (1). Если задан угловой коэффициент k= k1, то уравнение прямой будет находить в форме (3): y =k1 x+ b. Неизвестный коэффициент b найдем из условия y0 = k 1 x0 + b (точка М0 принадлежит прямой). Найденное b= y0 – k 1 x0 подставим в уравнение y =k1 x+ b. Искомое уравнение прямой запишем в виде:
, то такая прямая описывается уравнением (1). Если задан угловой коэффициент k= k1, то уравнение прямой будет находить в форме (3): y =k1 x+ b. Неизвестный коэффициент b найдем из условия y0 = k 1 x0 + b (точка М0 принадлежит прямой). Найденное b= y0 – k 1 x0 подставим в уравнение y =k1 x+ b. Искомое уравнение прямой запишем в виде:
y– y 0= k1 ( x– x 0). (6)
Пример. Написать уравнение прямой, проходящей через точку Q(2,7) параллельно прямой 2х-4у+3=0.
Решение. Найдем угловой коэффициент прямой 2 х–4у +3=0:
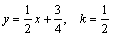 .
.
Для искомой прямой угловой коэффициент будет таким же, так как прямые параллельны. Подставим данные в уравнение (6):
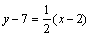 .
.
4. Угол между двумя прямыми
| Даны уравнения двух прямых. Требуется найти угол между ними. Угол между двумя непараллельными прямыми α1 и α2 найдем как угол между направляющими векторами этих прямых при задании канонических уравнений для α1 и α2, или же как угол между их нормалями, если заданы общие уравнения прямых α1 и α2. |
Пусть заданы две прямые α1: 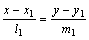 и α2:
и α2: 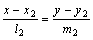 .
.
Направляющие векторы этих прямых: 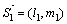 и
и 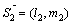 .
.
Угол φ между прямыми найдем из скалярного произведения векторов 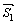 и
и 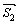 :
: 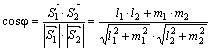 .
.
Пусть заданы общие уравнения прямых 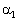 и
и 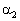 : А1х+В1у+С1 = 0 и А 2х+В 2у+С 2=0. Тогда нормали к этим прямым:
: А1х+В1у+С1 = 0 и А 2х+В 2у+С 2=0. Тогда нормали к этим прямым: 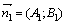 и
и 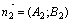 , и
, и  .
.
Если 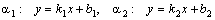 , то из
, то из 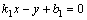 и
и 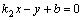 следует:
следует: 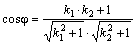 .
.
Условием перпендикулярности прямых будет соответственно:
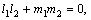 либо
либо 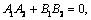 либо
либо 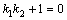 .
.
Из последнего равенства следует, что 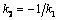 . Таким образом угловые коэффициенты двух перпендикулярных прямых обратные по величине и противоположны по знаку.
. Таким образом угловые коэффициенты двух перпендикулярных прямых обратные по величине и противоположны по знаку.
Условием параллельности прямых будет соответствовать:
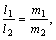 либо
либо 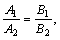 либо
либо 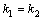 .
.
5. Расстояние от точки до прямой
Дана прямая Ах+Ву+С=0 и точка Q(х1, у1). Требуется найти расстояние от точки Q до прямой. Это расстояние находится по формуле:
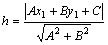 (7)
(7)
Пример. Даны вершины треугольника АВС: А(–2,3), В(1,12), С(11,6). Найти: 1) уравнение стороны АВ; 2) уравнение высоты СD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ; 4) уравнение окружности, для которой медиана АЕ служит диаметром.
Решение. 1. Уравнение прямой, проходящей через точку А(х1, у1) и В(х2, у2), имеет вид 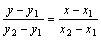 . Чтобы найти уравнение стороны АВ, подставим координаты точек А и В в уравнение прямой:
. Чтобы найти уравнение стороны АВ, подставим координаты точек А и В в уравнение прямой:
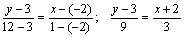 ; у –3=3х +6; у=3 х+9 (АВ).
; у –3=3х +6; у=3 х+9 (АВ).
2. Высота СD перпендикулярна стороне АВ, а потому их угловые коэффициенты kCD и kAB удовлетворяют условию 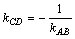 . Из уравнения прямой АВ следует, что kAB =3, тогда
. Из уравнения прямой АВ следует, что kAB =3, тогда 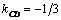 .
.
Напишем уравнение прямой, проходящей через данную точку в данном направлении: y – y1 =k (x– x 1) . Подставив в уравнение координаты точки С и угловой коэффициент kCD получим искомое уравнение высоты СD:
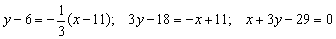 (СD).
(СD).
3. Определим координаты точки Е. Применяем формулы деления отрезка пополам: 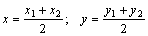 . Используя координаты вершин В и С получаем:
. Используя координаты вершин В и С получаем:
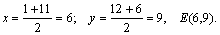
По точкам А и Е построим уравнение медианы АЕ:
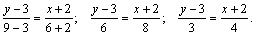
4. Уравнение окружности радикса R с центром в точке К(а,b) имеет вид ( х–а)2 +(у–b) 2= R2.
Так как по условию медиана АЕ является диаметром искомой окружности; то центр окружности К делит отрезок АЕ пополам. Находим координаты точки К: