Объем шара, ограниченного сферой
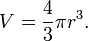
Площадь сегмента сферы
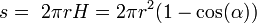 , где H — высота сегмента, а
, где H — высота сегмента, а 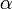 — зенитный угол
— зенитный угол
Билет 23.1
Синусом называется отношение 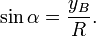
Косинусом называется отношение 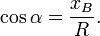
Тангенс определяется как 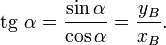
Котангенс определяется как 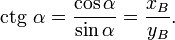
Секанс определяется как 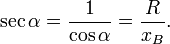
Функции 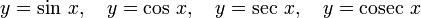 — периодические с периодом 2π, функции
— периодические с периодом 2π, функции 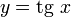 и
и 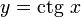 — c периодом π.
— c периодом π.
23.2
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Если касательная плоскость к сфере определяется как плоскость, имеющая со сферой единственную общую точку, то признак и свойство касательной плоскости формулирутся так:
Признак. Если плоскость проходит через точку сферы перпендикулярно радиусу, проведенному в эту точку, то плоскость касается сферы.
Свойство. Касательная плоскость перпендикулярна радиусу сферы, проведенному в точку касания.
Если же касательная плоскость к сфере определяется как плоскость, проходящая через точку на сфере перпендикулярно радиусу, проведенному в эту точку, то формулировки признака и свойства таковы:
Признак. Если плоскость имеет со сферой единственную общую точку, то она перпендикулярна радиусу, проведенному в эту точку, т.е. является касательной плоскостью.
Свойство. Касательная плоскость имеет со сферой единственную общую точку
Билет 24.1
Градусная мера.Здесь единицей измерения является градус ( обозначение ° ) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. Один градус состоит из 60 минут ( их обозначение ‘ ); одна минута – соответственно из 60 секунд ( обозначаются “ ).
Радианная мера. Как мы знаем из планиметрии длина дуги l, радиус r и соответствующий центральный угол 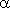 связаны соотношением:
связаны соотношением:
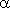 = l / r .
= l / r .
Эта формула лежит в основе определения радианной меры измерения углов. Так, если l = r , то 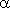 = 1, и мы говорим, что угол
= 1, и мы говорим, что угол 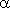 равен 1 радиану, что обозначается:
равен 1 радиану, что обозначается: 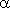 = 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:
= 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:
Радиан есть центральный угол, у которого длина дуги и радиус равны ( AmB = AO, рис.1 ). Итак, радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.
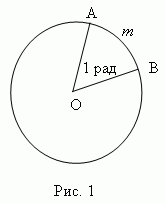
Следуя этой формуле, длину окружности C и её радиус r можно выразить следующим образом:
2  = C / r .
= C / r .
Так, полный оборот, равный 360° в градусном измерении, соответствует2  в радианном измерении. Откуда мы получаем значение одного радиана:
в радианном измерении. Откуда мы получаем значение одного радиана:
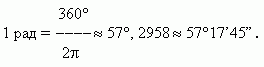
Обратно,
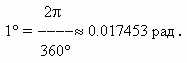
Полезно помнить следующую сравнительную таблицу значений наиболее часто встречающихся углов в градусах и радианах:
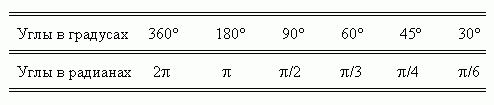
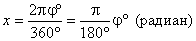 ;
; 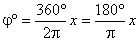 ,
,
24.2
надо умножить площадь основания на высоту призмы
Билет 25.1
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Правило исследования функции y=f(x) на экстремум
1. Найти область определения функции f(x).
2. Найти первую производную функции f '(x).
3. Определить критические точки, для этого:
a. найти действительные корни уравнения f '(x)=0;
b. найти все значения x при которых производная f '(x) не существует.
4. Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
5. Вычислить значение функции в точках экстремума.
ПРИМЕР!
25.2
Vпрямоугольного параллелепипедаV= SH= abc
Билет 26.1
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] .
в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = 2 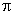 .
.
д) Нули функции: sin x = 0 при x = 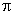 n, n
n, n 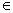 Z.
Z.
е) Промежутки знакопостоянства:
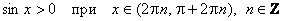 ;
; 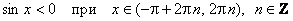 .
.
ж) Промежутки монотонности:
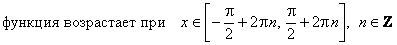 ;
;
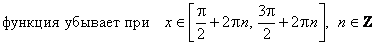 .
.
з) Экстремумы:
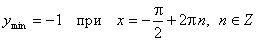 ;
; 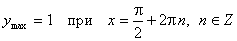 .
.
График функции y= sin x изображен на рисунке.
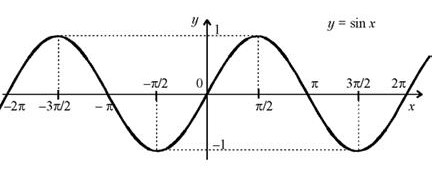
26.2
V цилиндра Pr2 * H
Билет 27.1
а) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] .
в) Четность, нечетность: функция четная.
г) Периодичность: функция периодическая с основным периодом T = 2 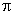 .
.
д) Нули функции: cos x = 0 при x = 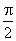 +
+ 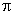 n, n
n, n 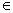 Z.
Z.
е) Промежутки знакопостоянства:
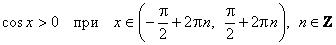 ;
;
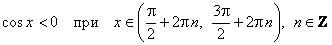 .
.
. ж) Промежутки монотонности:
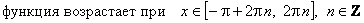 ;
;
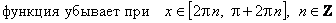 .
.
з) Экстремумы:
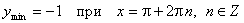 ;
; 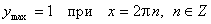 .
.
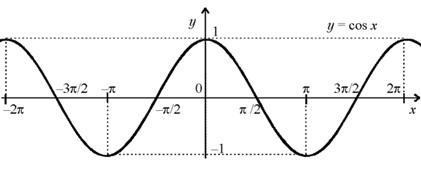
График функции y= cos x изображен на рисунке.
27.2

Билет 28.1
а) Область определения: D (tg x) = R\ { 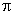 /2 +
/2 + 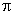 n( n
n( n 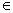 Z) }.
Z) }.
б) Множество значений: E (tg x ) = R .
в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = 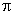 .
.
д) Нули функции: tg x = 0 при x = 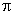 n, n
n, n 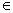 Z.
Z.
е) Промежутки знакопостоянства:
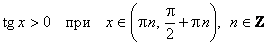 ;
; 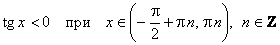 .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y= tg x изображен на рисунке.
28.2 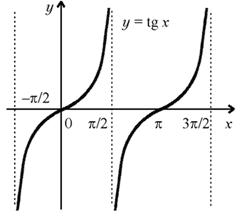
29.1
