Определение возрастающей функции.
Функция y = f(x) возрастает на интервале X, если для любых 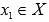 и
и 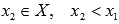 выполняется неравенство
выполняется неравенство 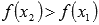 . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y = f(x) убывает на интервале X, если для любых 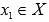 и
и 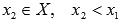 выполняется неравенство
выполняется неравенство 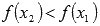 . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
14.2
Площадь боковой поверхности произвольной призмы 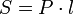 , где
, где 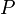 — периметр перпендикулярного сечения,
— периметр перпендикулярного сечения, 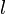 — длина бокового ребра.
— длина бокового ребра.
Площадь боковой поверхности правильной призмы 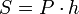 , где
, где 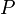 — периметр основания призмы, ,
— периметр основания призмы, , 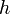 — высота призмы
— высота призмы
Билет 15.1
Вектор - это направленный отрезок.
Суммой векторов − 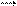 a(a1;a2) и −
a(a1;a2) и − 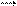 b(b1;b2) называется вектор −
b(b1;b2) называется вектор − 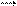 c
c 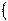 a1+b1;a2+b2
a1+b1;a2+b2 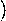 ,
,
т.е. − 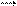 a
a 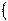 a1;a2
a1;a2 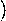 +−
+− 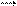 b
b 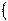 b1;b2
b1;b2 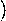 =−
=− 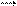 c
c  a1+b1;a2+b2
a1+b1;a2+b2  .
.
Определение 1.Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.
(Масса тела, объем, время и т.д.)
Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.
1) Сложение векторов.
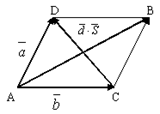
Опр. 6.Суммой двух векторов  и
и 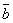 является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения(правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения(правило параллелограмма).
 Свойства сложения.
Свойства сложения.
1о.  +
+ 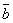 =
= 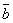 +
+  (переместительный закон).
(переместительный закон).
2о.  + (
+ ( 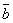 +
+ 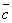 ) = (
) = (  +
+ 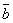 ) +
) + 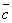 = (
= (  +
+ 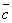 ) +
) + 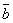 (сочетательный закон).
(сочетательный закон).
3о.  + (–
+ (–  ) +
) + 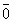 .
.
2) Вычитание векторов.
Опр. 9.Подразностью векторов  и
и 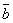 понимают вектор
понимают вектор 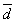 =
=  –
– 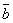 такой, что
такой, что 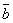 +
+ 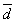 =
=  .
.
В параллелограмме – это другая диагональ СД
3) Умножение вектора на число.
Опр. 10. Произведениемвектора  на скаляр k называется вектор
на скаляр k называется вектор
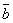 =k
=k  =
=  k,
k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора  , если k > 0;
, если k > 0;
2. противоположно направлению вектора  , если k < 0;
, если k < 0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k+l)  =k
=k  +l
+l  .
.
k(  +
+ 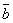 ) =k
) =k  +k
+k 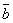 .
.
2o. k(l  ) = (kl)
) = (kl)  .
.
3o. 1×  =
=  , (–1)×
, (–1)×  = –
= –  , 0×
, 0×  =
= 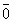 .
.
15.2
Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину[1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.
Объём пирамиды может быть вычислен по формуле:
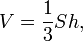
где 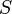 — площадь основания и
— площадь основания и 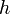 — высота;
— высота;
Боковая поверхность — это сумма площадей боковых граней:
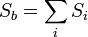
Полная поверхность — это сумма боковой поверхности и площади основания:
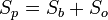
Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
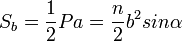
где 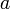 — апофема ,
— апофема , 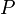 — периметр основания,
— периметр основания, 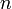 — число сторон основания,
— число сторон основания, 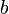 — боковое ребро,
— боковое ребро, 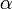 — плоский угол при вершине пирамиды.
— плоский угол при вершине пирамиды.
Объем пирамиды
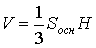
где Sосн - площадь основания, H - высота.
Площадь боковой поверхности пирамиды равна сумме площадей её боковых граней.
Площадь полной поверхности пирамиды
Sп=Sб+2Sосн,
где Sб - площадь боковой поверхности прямой пирамиды, Sосн - площадь основания.
Площадь боковой поверхности правильной пирамиды
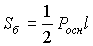
где Pосн - периметр основания правильной пирамиды, l - её апофема.
Билет 16.1
Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве.
Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:
1. Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):
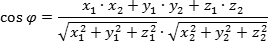
2. Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
3. Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).
16.3
Площадь боковой поверхности правильной пирамиды
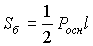
где Pосн - периметр основания правильной пирамиды, l - её апофема.
Билет 17.1
Скалярным произведением двух ненулевых векторов a и b называется число (скаляр), равный произведению длин этих векторов на косинус угла φ между ними. Скалярное произведение можно обозначать различными способами, например, как ab, a · b, (a , b), (a · b). Таким образом, скалярное произведение равно:
a · b = |a| · |b| · cos φ
Если хотя бы один из векторов равен нулю, то скалярное произведение равно нулю.
· Свойство перестановки: a · b = b · a (от перестановки множителей скалярное произведение не меняется);
· Свойство распределения: a · (b · c) = (a · b) · c (результат не зависит от порядка умножения);
· Свойство сочетания (по отношению кскалярному множителю): (λ a) · b = λ (a · b).
· Свойство ортогональности (перпендикулярности): если вектора a и b ненулевые, то их скалярное произведение равно нулю, только когда эти векторы ортогональны (перпердикулярны друг к другу)a ┴ b;
· Свойство квадрата: a · a = a2 = |a|2 (скалярное произведения вектора самого с собой равняется квадрату его модуля);
· Если координаты векторов a={x1, y1, z1} и b={x2, y2, z2}, то скалярное произведение равно a · b = x1x2 + y1y2 + z1z2.
17.2
Усечё́нная пирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию.
