Полином Жегалкина -это еще один способ выразить произвольную булеву функцию через бинарные операции.

Булевы функции

Булева функция – это функция, и аргументы и значение которой принадлежит множеству { 0, 1 } ( от 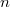переменных- отображение → ).

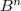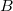Логической ( булевой) функцией (или просто функцией) n переменных y = f(x₁, x₂, …, x_n) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

Заметим, что логическая переменная х может подразумевать под числом 0 некоторое высказывание, которое ложно, и под числом 1 высказывание, которое истинно.

функция п переменных – это отображение Е^п в Е,которое можно задать непосредственно таблицей, называемой таблицей истинности данной функции.

важные функции двух переменных

1) конъюнкция (функция И) ( x&y или xÙy;) 7) стрелка Пирса (иногда эту функцию называют штрих Лукасевича)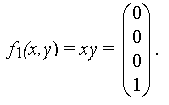

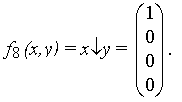
2) дизъюнкция (функция или)

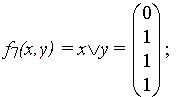
3) импликация (следование) x ®y

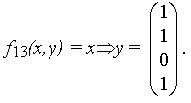
4) сложение по модулю 2

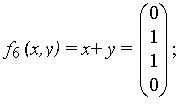
6) штрих Шеффера

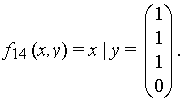
ДНФ

Для любой булевой функции можно построить ее таблицу истинности. Но и по таблице истинности можно восстановить булеву функцию.

СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА

Возьмем наборы переменных, на которых функция равна единице. Если значение переменной в этом наборе равно 0, то эта переменная берется с отрицанием. Если значение переменной в этом наборе равно 1, то эта переменная берется без отрицания.Соединив все переменные, соответствующие этому набору, через знак & (причем сам знак & для краткости будем опускать), мы получим элементарную конъюнкцию. Тогда дизъюнкция всех элементарных конъюнкций, соответствующих наборам значений переменных,где функция равна единице, и восстанавливает исходную функцию.Это совершенная дизъюнктивная нормальная форма (СДНФ) нашей функции.

ДНФ (Дизъюнктивная Нормальная Форма) — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.

СДНФ (Совершенная Дизъюнктивная Нормальная Форма)— это такая ДНФ, которая удовлетворяет условиям:

§ в ней нет одинаковых простых конъюнкций

§ каждая простая конъюнкция полная

КНФ

КНФ (Конъюнктивная Нормальная Форма) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

СКНФ (Совершенная Конъюнктивная Нормальная Форма)— это такая КНФ, которая удовлетворяет условиям:

§ в ней нет одинаковых простых дизъюнкций

§ каждая простая дизъюнкция полная

Возьмем наборы переменных, на которых функция равна нулю. Если значение переменной в этом наборе равно 0, то эта переменная берется без отрицания. Если значение переменной в этом наборе равно 1, то эта переменная берется с отрицанием. Соединив все переменные, соответствующие этому набору, через знак ., мы получим элементарную дизъюнкцию. Тогда конъюнкция всех элементарных дизъюнкций, соответствующих наборам значений переменных, где функция равна нулю, и восстанавливает исходную функцию. Это совершенная конъюнктивная нормальная форма (СКНФ) нашей функции.

2)минимальный днф/кнф, простые импликанты, сокращенный днф/кнф (определение и свойства)
теорема о том, что минимальный днф есть дизъюнкция простых импликантов тупиковый днф

Булеву функцию g назовем импликантом булевой функции f, если для любых наборов из 0 и 1 из равенства g = 1 следует равенство f = 1.

Если отбрасывание любой переменной импликанта приводит к тому, что полученная функция перестает быть импликантом, то такой импликант называется простым.

Сокращенная ДНФ функции f (сокр ДНФ f) есть дизъюнкция всех простых импликантов функции f. Всякая функция реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Сокращенная ДНФ: форма записи функции, обладающая следующими свойствами:

-Любые два слагаемых различаются как минимум в двух позициях

-Ни один из конъюнктов не содержится в другом.

Алгоритм построения сокращенной ДНФ с помощью СКНФ выглядит следующим образом.

1. По таблице истинности строим СКНФ функции f .

2. В СКНФ раскрываем скобки, удаляем дублирующие элементы

(A & A = A, A VA = A) и элементы, которые содержат переменную

вместе с ее отрицанием (A & –A = 0).

3. Проводим поглощение (A . AB = A) и удаляем дублирующие

элементы. Сокращенная ДНФ функции f получена.

Минимальная ДНФ — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных. Каждая минимальная ДНФ является сокращенной, но не каждая сокращенная — минимальна.

Если из дизъюнкции простых импликантов функции f нельзя отбросить ни одного слагаемого (иначе поменяется таблица истинности), то говорят, что получена тупиковая ДНФ (ТДНФ) функции f. ТупиковаяДНФ функции f, содержащая минимальное число переменных или их отрицаний, называется минимальной ДНФ (МДНФ) функции f.

Минимальная ДНФ функции является дизъюнкцией простых импликантов этой функции.

Доказательство. Будем рассуждать от противного. Предположим, что в минимальную ДНФ входит непростой импликант. Рассмотрим ДНФ, которая получается из минимальной ДНФ функции заменой этого непростого импликанта на простой, полученный из него опусканием некоторых букв. Полученная ДНФ будет содержать меньшее число букв и все еще реализовывать функцию (обоснуйте!), что противоречит предположению о минимальности исходной ДНФ.

3) монотонные функции. теорема о строении сокращенного днф для монотонной функции

Монотонность: Функция f(x1, x2, …, xn) называется монотонной, если для всяких наборов a = (a1, …, an) и b= (b1, …, bn) условие a Ј b влечет f(a) Ј f(b).

Функция монотонна тогда и только тогда, когда ее сокращенная ДНФ не содержит отрицаний.

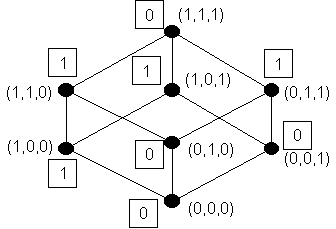
Рассмотрим задачу: выяснить будет ли функция f(x₁,x₂,x₃)=x₁+x₂×x₃ монотонной? Для решения этой задачи удобно начертить диаграмму частично упорядоченного множества B³ и в вершинах этой диаграммы проставить значения функции f(x₁,x₂,x₃). Такая диаграмма приведена на рис. 2.1, значения функции f(x₁,x₂,x₃) заключены в квадрат, чтобы их отличать от обозначения вершин множества B³.

4) Многочлены(полином) Жигалкина

Булевы функции

Булева функция – это функция, и аргументы и значение которой принадлежит множеству { 0, 1 } ( от переменных- отображение → ).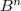

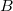Логической ( булевой) функцией (или просто функцией) n переменных y = f(x₁, x₂, …, x_n) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

Заметим, что логическая переменная х может подразумевать под числом 0 некоторое высказывание, которое ложно, и под числом 1 высказывание, которое истинно.

функция п переменных – это отображение Е^п в Е,которое можно задать непосредственно таблицей, называемой таблицей истинности данной функции.

важные функции двух переменных

1) конъюнкция (функция И) ( x&y или xÙy;) 7) стрелка Пирса (иногда эту функцию называют штрих Лукасевича)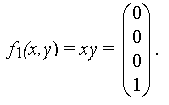

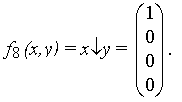
2) дизъюнкция (функция или)

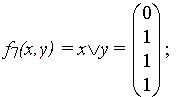
3) импликация (следование) x ®y

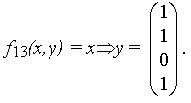
4) сложение по модулю 2

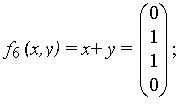
6) штрих Шеффера

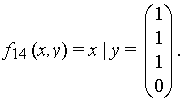
ДНФ

Для любой булевой функции можно построить ее таблицу истинности. Но и по таблице истинности можно восстановить булеву функцию.

СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА

Возьмем наборы переменных, на которых функция равна единице. Если значение переменной в этом наборе равно 0, то эта переменная берется с отрицанием. Если значение переменной в этом наборе равно 1, то эта переменная берется без отрицания.Соединив все переменные, соответствующие этому набору, через знак & (причем сам знак & для краткости будем опускать), мы получим элементарную конъюнкцию. Тогда дизъюнкция всех элементарных конъюнкций, соответствующих наборам значений переменных,где функция равна единице, и восстанавливает исходную функцию.Это совершенная дизъюнктивная нормальная форма (СДНФ) нашей функции.

ДНФ (Дизъюнктивная Нормальная Форма) — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.

СДНФ (Совершенная Дизъюнктивная Нормальная Форма)— это такая ДНФ, которая удовлетворяет условиям:

§ в ней нет одинаковых простых конъюнкций

§ каждая простая конъюнкция полная

КНФ

КНФ (Конъюнктивная Нормальная Форма) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

СКНФ (Совершенная Конъюнктивная Нормальная Форма)— это такая КНФ, которая удовлетворяет условиям:

§ в ней нет одинаковых простых дизъюнкций

§ каждая простая дизъюнкция полная

Возьмем наборы переменных, на которых функция равна нулю. Если значение переменной в этом наборе равно 0, то эта переменная берется без отрицания. Если значение переменной в этом наборе равно 1, то эта переменная берется с отрицанием. Соединив все переменные, соответствующие этому набору, через знак ., мы получим элементарную дизъюнкцию. Тогда конъюнкция всех элементарных дизъюнкций, соответствующих наборам значений переменных, где функция равна нулю, и восстанавливает исходную функцию. Это совершенная конъюнктивная нормальная форма (СКНФ) нашей функции.

2)минимальный днф/кнф, простые импликанты, сокращенный днф/кнф (определение и свойства)
теорема о том, что минимальный днф есть дизъюнкция простых импликантов тупиковый днф

Булеву функцию g назовем импликантом булевой функции f, если для любых наборов из 0 и 1 из равенства g = 1 следует равенство f = 1.

Если отбрасывание любой переменной импликанта приводит к тому, что полученная функция перестает быть импликантом, то такой импликант называется простым.

Сокращенная ДНФ функции f (сокр ДНФ f) есть дизъюнкция всех простых импликантов функции f. Всякая функция реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Сокращенная ДНФ: форма записи функции, обладающая следующими свойствами:

-Любые два слагаемых различаются как минимум в двух позициях

-Ни один из конъюнктов не содержится в другом.

Алгоритм построения сокращенной ДНФ с помощью СКНФ выглядит следующим образом.

1. По таблице истинности строим СКНФ функции f .

2. В СКНФ раскрываем скобки, удаляем дублирующие элементы

(A & A = A, A VA = A) и элементы, которые содержат переменную

вместе с ее отрицанием (A & –A = 0).

3. Проводим поглощение (A . AB = A) и удаляем дублирующие

элементы. Сокращенная ДНФ функции f получена.

Минимальная ДНФ — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных. Каждая минимальная ДНФ является сокращенной, но не каждая сокращенная — минимальна.

Если из дизъюнкции простых импликантов функции f нельзя отбросить ни одного слагаемого (иначе поменяется таблица истинности), то говорят, что получена тупиковая ДНФ (ТДНФ) функции f. ТупиковаяДНФ функции f, содержащая минимальное число переменных или их отрицаний, называется минимальной ДНФ (МДНФ) функции f.

Минимальная ДНФ функции является дизъюнкцией простых импликантов этой функции.

Доказательство. Будем рассуждать от противного. Предположим, что в минимальную ДНФ входит непростой импликант. Рассмотрим ДНФ, которая получается из минимальной ДНФ функции заменой этого непростого импликанта на простой, полученный из него опусканием некоторых букв. Полученная ДНФ будет содержать меньшее число букв и все еще реализовывать функцию (обоснуйте!), что противоречит предположению о минимальности исходной ДНФ.

3) монотонные функции. теорема о строении сокращенного днф для монотонной функции

Монотонность: Функция f(x1, x2, …, xn) называется монотонной, если для всяких наборов a = (a1, …, an) и b= (b1, …, bn) условие a Ј b влечет f(a) Ј f(b).

Функция монотонна тогда и только тогда, когда ее сокращенная ДНФ не содержит отрицаний.

Рассмотрим задачу: выяснить будет ли функция f(x₁,x₂,x₃)=x₁+x₂×x₃ монотонной? Для решения этой задачи удобно начертить диаграмму частично упорядоченного множества B³ и в вершинах этой диаграммы проставить значения функции f(x₁,x₂,x₃). Такая диаграмма приведена на рис. 2.1, значения функции f(x₁,x₂,x₃) заключены в квадрат, чтобы их отличать от обозначения вершин множества B³.

4) Многочлены(полином) Жигалкина

Полином Жегалкина -это еще один способ выразить произвольную булеву функцию через бинарные операции.

Полином Жегалкина — полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или.

Полином Жегалкина имеет следующий вид:

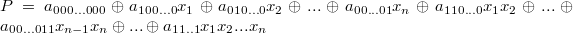
Полином Жегалкина имеет следующий вид:

1.

§

§

§

§

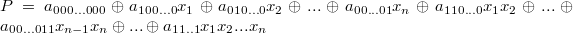
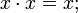
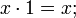
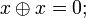
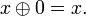
5) Замкнутые классы, монотонные, линейные, самосопряженные

Класс булевых функций 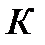называется замкнутым, если он совпадает со своим замыканием, т.е. .

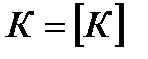Если любая булева функция, являющаяся суперпозицией функций некоторого множества принадлежит этому множеству, то такое множество называют замкнутым.

Класс булевых функций C называется замкнутым классом (классом Поста), если он вместе со всякими своими функциями содержит любую их суперпозицию.

Суперпозиция (сложная функция) — это функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных.

Пример:

Исходные функции:

1.

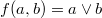
2.

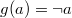
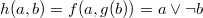— подстановка функции 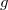вместо второго аргумента функции 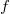. В данном примере при помощи подстановки мы получили функцию .

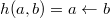Для произвольного класса системы двоичных функций 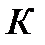множество всех двоичных функций, представимых формулами ,над 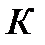, называется замыканием класса (системы) функций 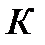и обозначается через .

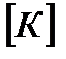Имеют место следующие свойства замыкания:

Свойство 3.1.2. .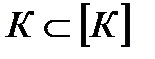

Свойство 3.1.3.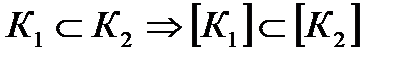

Свойство 3.1.4.